数学八年级上册5.2 平面直角坐标系图文ppt课件

这是一份数学八年级上册5.2 平面直角坐标系图文ppt课件，共22页。PPT课件主要包含了北京西路，北京东路，中山北路，中山南路，第一象限，第二象限，第四象限，第三象限，课堂练习，5－4等内容，欢迎下载使用。

　　我们曾经利用数轴上的实数来表示直线上的点．
思考：　　类似地，能否找到一种方法来表示平面内点的位置呢？
5.2　平面直角坐标系（1）
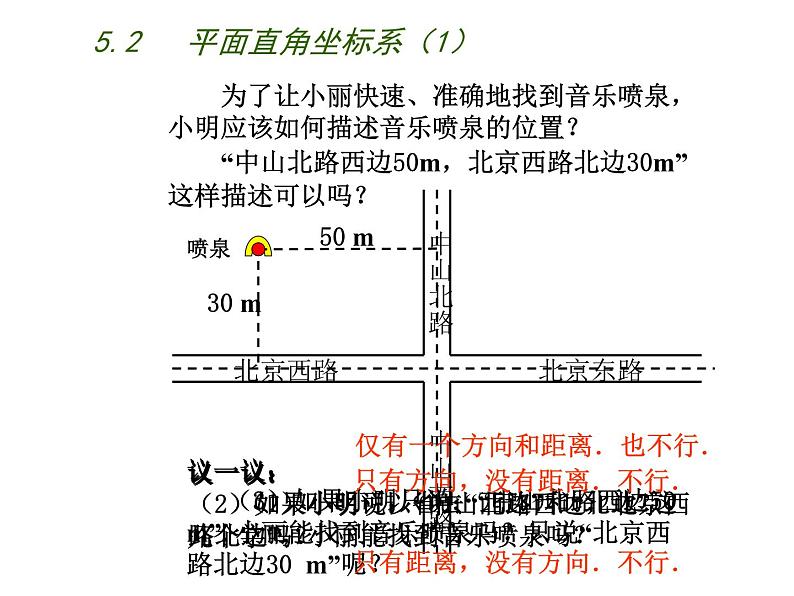
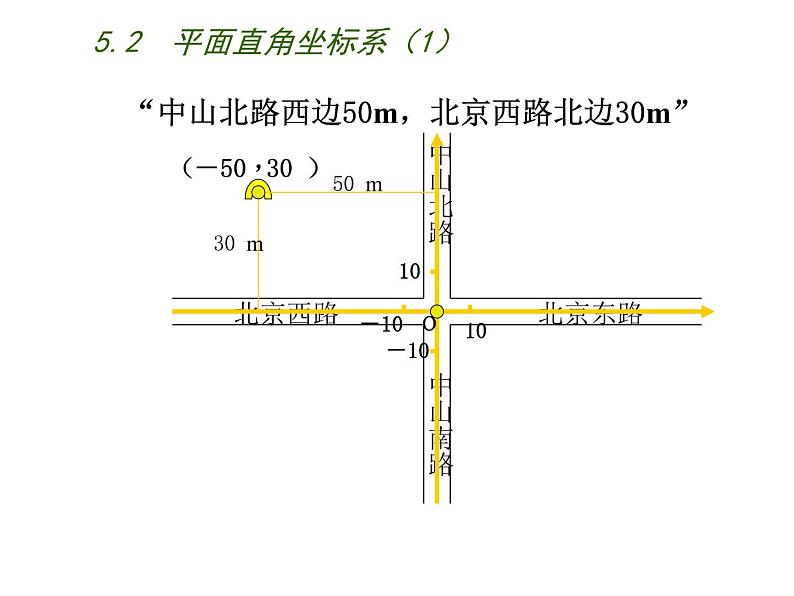
　　“中山北路西边50m，北京西路北边30m”
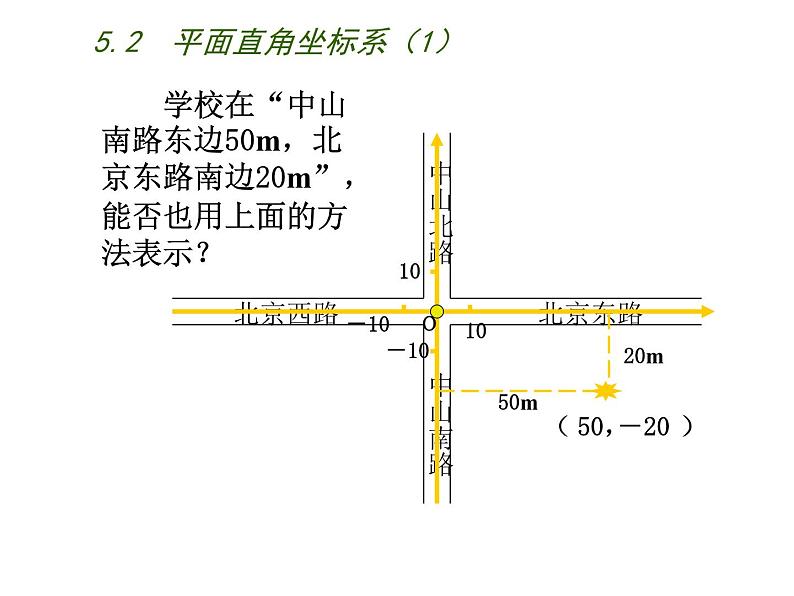
　　学校在“中山南路东边50m，北京东路南边20m”，能否也用上面的方法表示？
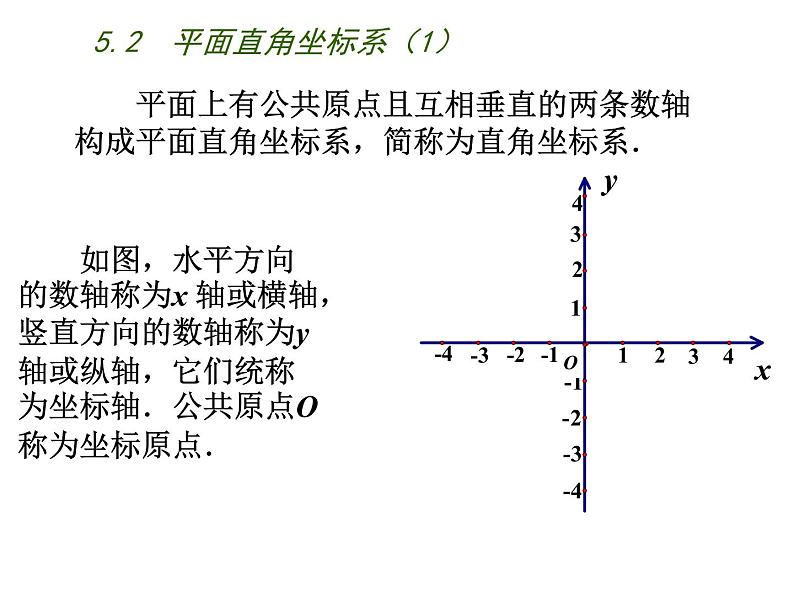
　　平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系，简称为直角坐标系．
　　如图，水平方向的数轴称为x 轴或横轴，竖直方向的数轴称为y 轴或纵轴，它们统称为坐标轴．公共原点O称为坐标原点．
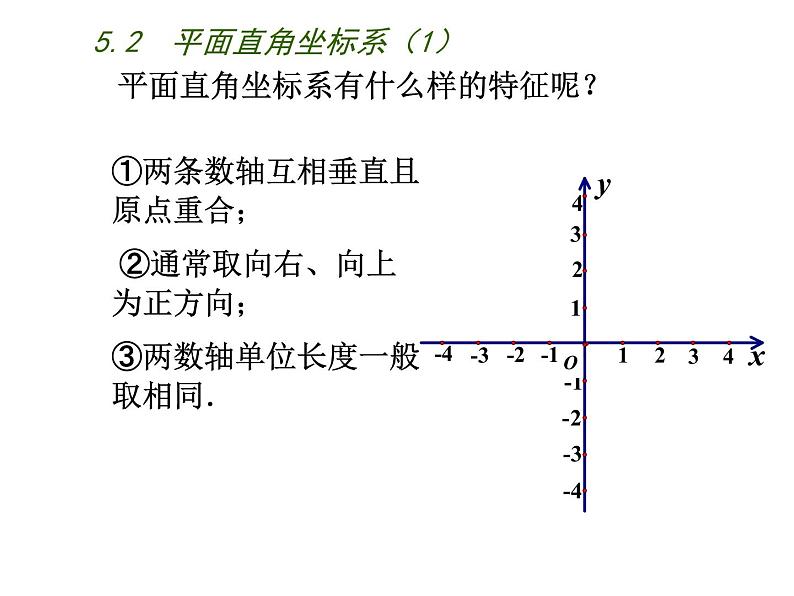
平面直角坐标系有什么样的特征呢？
①两条数轴互相垂直且原点重合； ②通常取向右、向上为正方向； ③两数轴单位长度一般取相同．
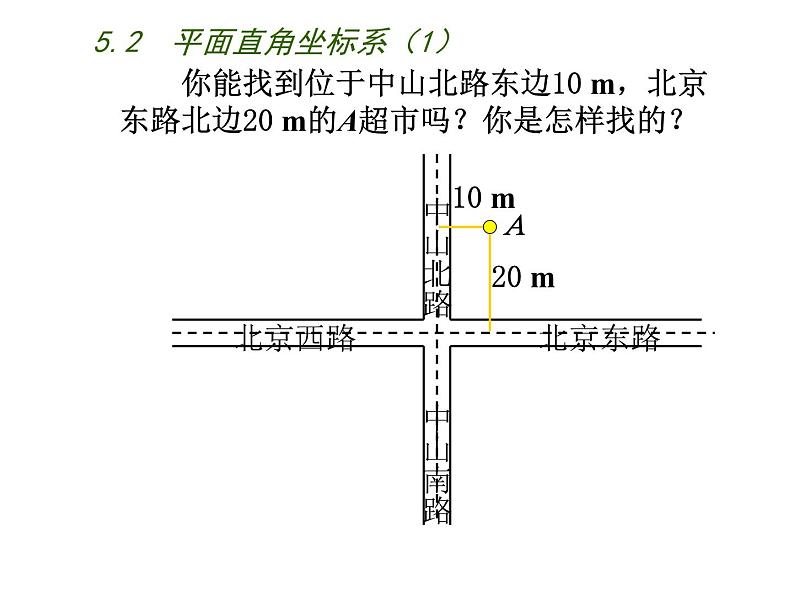
　　你能找到位于中山北路东边10 m，北京东路北边20 m的A超市吗？你是怎样找的？
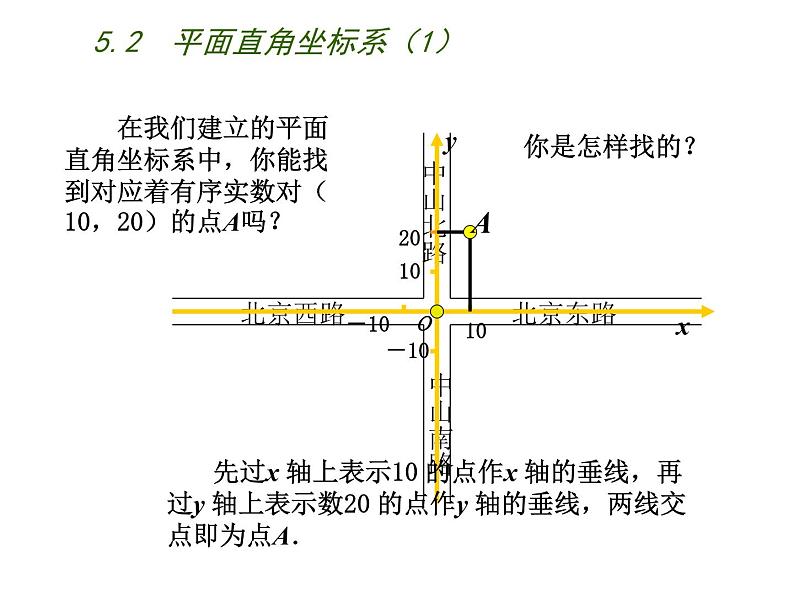
　　在我们建立的平面直角坐标系中，你能找到对应着有序实数对（10，20）的点A吗？
　 先过x 轴上表示10 的点作x 轴的垂线，再过y 轴上表示数20 的点作y 轴的垂线，两线交点即为点A．
　　通过上面的讨论，你有什么发现？ 在直角坐标系内，点与有序实数对具有怎样的关系？
　　在直角坐标系中，一对有序实数可以确定一个点的位置；反之，任意一点都可以用一对有序实数表示．
　　我们称这样的有序实数对叫做点的坐标.
　 在平面直角坐标系中，有序实数对（a，b）描述的是一个点 P 的位置，该如何确定点 P 的位置呢？
　　过 x 轴上表示 a的点作 x 轴的垂线，再过 y 轴上表示 b 的点作 y 轴的垂线，两线的交点即为点 P .
　 如图，已知平面内一点Q，你能确定与它相应的一对有序实数（m，n）吗？
　过点 Q 分别作 x 轴，y 轴的垂线，将垂足对应的数组合起来形成一对有序实数，即为点 Q 的坐标，可表示为 Q（m，n）.
1．在平面直角坐标系中，一对有序实数可以确 定一个点的位置；反之，任意一点的位置都可以用一对有序实数来表示．这样的有序实数对叫做点的坐标．
2．点的坐标通常与表示该点的大写字母写在一起，如 P（a，b），Q（m，n）.
例1 　在直角坐标系中，描出下列各点的位置：A(4，1)，B(－1，4)，C(－4，－2)，D(3，－2)，E(0，1 )，F( －4，0 ) ．
例 2　写出图中点A、B、C 的坐标．
注意：坐标轴上的点不在任一象限内．
　　你能指出点A、B、C、D分别在第几象限吗？点E、F呢？
在x轴上的点，纵坐标等于0；
在y轴上的点，横坐标等于0；
二、判断：1．对于坐标平面内的任一点，都有唯 一的一对有序实数与它对应.（ 　）2．在直角坐标系内，原点的坐标是0.（ 　）　3．点 A（a ，－b ）在第二象限，则点B（－a , b ）在第四象限. （ 　）4．若点 P 的坐标为（a，b），且 a·b ＝0，则点 P 一定在坐标原点. （ ）
一、课本 P 122第1、2题．
探索点的坐标的几何意义：
　　已知点A（a，b），过点A作x轴的垂线，垂足为B，过点A作y轴的垂线，垂足为C. （1） 四边形OBAC是矩形吗？ （2） 线段AB的长度与点A的坐标有什么数量关系？ （3） 线段AC的长度与点A的坐标有什么数量关系？
三、已知 P 点坐标为（2 a ＋ 1，a－3）( 1 ) 点 P 在 x 轴上，则 a＝ ；( 2 ) 点 P 在 y 轴上，则 a＝ ；
四、若点 P（x，y）在第四象限，| x |＝5，| y |＝4，则 P 点的坐标为 .
小结与反思：　　这节课你学到了什么？
1．什么是平面直角坐标系?2．平面内点的坐标的意义,你理解了吗?3．在学习过程中你还存在哪些问题?
1．课本129页1、2．2．补充习题．