第二章轴对称图形复习题课件-(苏科版)

这是一份第二章轴对称图形复习题课件-(苏科版)，共34页。

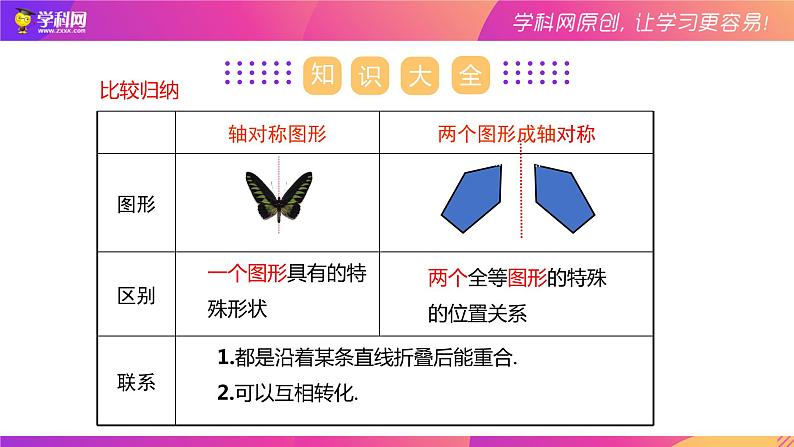
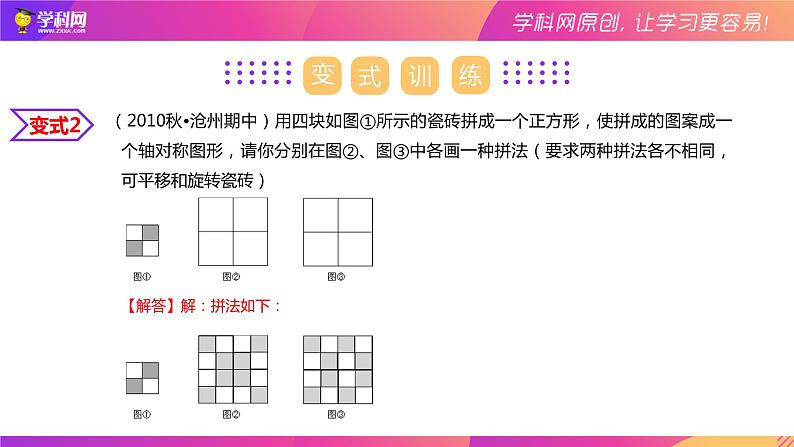
第二章《轴对称图形》章节复习（苏科版）1轴对称与轴对称图形 如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.轴对称图形轴对称图形对称轴对称轴am比较归纳一个图形具有的特殊形状两个全等图形的特殊的位置关系1.都是沿着某条直线折叠后能重合.2.可以互相转化.例1（2018秋•潜山市期末）数学在我们的生活中无处不在，就连小小的台球桌上都有数学问题．如图所示，∠1＝∠2．若∠3＝25°，为了使白球反弹后能将黑球直接撞入底袋中，那么击打白球时，必须保证∠1为（　　）A．65° B．75° C．55° D．85°【解答】解：∵由题意可得：∠2+∠3＝90°，∠3＝25°，∴∠2＝65°，∵∠1＝∠2，∴∠1＝65°．故选：A．变式1（2017春•景泰县期末）在线段、角、圆、等腰三角形、平行四边形、正方形中不是轴对称图形的是　 　．【解答】解：线段是轴对称图形；角是轴对称图形；等腰三角形是轴对称图形；平行四边形不是轴对称图形；正方形是轴对称图形．故答案为：平行四边形．变式2（2010秋•沧州期中）用四块如图①所示的瓷砖拼成一个正方形，使拼成的图案成一个轴对称图形，请你分别在图②、图③中各画一种拼法（要求两种拼法各不相同，可平移和旋转瓷砖）【解答】解：拼法如下：2轴对称的性质 类似地，轴对称图形的对称轴，是任何一对对称点所连线段的垂直平分线.轴对称图形的性质如图，MN垂直平分AA ′, MN垂直平分BB ′.例2（2020春•青白江区期末）如图，在边长为1的小正方形组成的网格中，点A，B，C均在小正方形的顶点上．（1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′；（2）求△ABC的面积．变式1（2019春•市南区期中）如图，点A、B、C都在6×6的方格纸的格点上，若该方格纸上还有一格点D，使得格点A、B、C、D能组成一个轴对称图形，则满足条件的格点D的个数有（　　）A．1个 B．2个 C．3个 D．4个【解答】解：如图所示，点D1，D2，D3即为所求．故选：C．变式2（2020春•沙坪坝区校级期末）如图，将长方形纸片ABCD沿AE向上折叠，使点B落在DC边上的点F 处．若∠FEC＝28°，则∠EAB 度数的值为（　　）A．12° B．14° C．16° D．18°【解答】解：由折叠得到∠BFA＝∠FEA，∵∠FEC＝28°，∴∠AEB＝（180°﹣28°）÷2＝76°，∴∠EAB＝90°﹣∠AEB＝14°．故选：B．3角平分线的性质和判定 性质定理： 角的平分线上的点到角的两边的距离相等.应用所具备的条件：定理的作用： 证明线段相等.应用格式：∵OP 是∠AOB的平分线，∴PD = PE（在角的平分线上的点到这个角的两边的距离相等）.推理的理由有三个，必须写完全，不能少了任何一个.PD⊥OA,PE⊥OB，3角平分线的性质和判定判定定理：角的内部到角的两边的距离相等的点在角的平分线上.应用所具备的条件：定理的作用：判断点是否在角平分线上.应用格式：∵ PD⊥OA,PE⊥OB，PD=PE.∴点P 在∠AOB 的平分线上.例3（2020春•高明区期末）如图，在Rt△ABC中∠C＝90°，BD是∠ABC的平分线，若CD＝4，AB＝14，则S△ABD＝（　　）A．56 B．28 C．14 D．12变式1（2020春•太原期末）如图，在△ABC中，∠ACB＝90°，AD平分∠BAC交BC于点D，CD＝3，DB＝5，点E在边AB上运动，连接DE，则线段DE长度的最小值为　　．【解答】解：当DE⊥AB时，线段DE的长度最小（根据垂线段最短），∵AD平分∠CAB，∠C＝90°，DE⊥AB，∴DE＝CD，∵CD＝3，∴DE＝3，即线段DE 的长度的最小值是3，故答案为：3．变式2（2019秋•蒙阴县期中）如图所示，在△ABC中，∠BAC＝90°，AD⊥BC于D，∠ACB的平分线交AD于E，交AB于F，FG⊥BC于G，请猜测AE与FG之间有怎样的关系，并说明理由．【解答】证明：∵CF是∠ACB的平分线，∠BAC＝90°，FG⊥BC，∴FA＝FG，∠AFC＝∠CED，∵∠AEF＝∠CED，∴∠AEF＝∠AFC，∴AE＝AF，∴AE＝FG，∵AD⊥BC，FG⊥BC，∴AE∥FG，∴AE＝FG，AE∥FG．4线段垂直平分线的性质和判定线段垂直平分线上的点到线段两个端点的距离相等．判定与一条线段两个端点距离相等的点，在这条线段的垂直平分线上．应用格式：∵　PA =PB，∴　点P 在AB 的垂直平分线上．作用：判断一个点是否在线段的垂直平分线上.性质例4（2019春•七星关区期末）如图，在△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD＝DE．（1）若∠C＝40°，求∠BAD的度数；（2）若AC＝5，DC＝4，求△ABC的周长．【解答】（1）解：∵EF垂直平分AC，∴AE＝CE，∴∠C＝∠EAC＝40°，∵AD⊥BC，BD＝DE，∴AB＝AE，∴∠B＝∠BEA＝2∠C＝80°，∴∠BAD＝90°﹣80°＝10°；（2）由（1）知：AE＝EC＝AB，∵BD＝DE，∴AB+BD＝DE+AE＝DE+CE＝DC，∴C△ABC＝AB+BC+AC＝2DC+AC＝2×4+5＝13．．变式1（2020•文成县二模）如图，在△ABC中，BD平分∠ABC，E是BC的中点，过点E作BC的垂线交BD于点F，连结CF．若∠A＝50°，∠ACF＝40°，则∠CFD的度数为（　　）A．30° B．45° C．55° D．60°【解答】解：∵BD平分∠ABC，∴∠ABD＝∠CBD，设∠ABD＝∠CBD＝x°，则∠CFD＝2x°，∵EF是BC的垂直平分线，∴BF＝CF，∴∠FCB＝∠CBD＝x°，∵∠A＝50°，∠ACF＝40°，∴50°+40°+x°+2x°＝180°，解得：x＝30，∴∠CFD＝2x°＝60°，故选：D．变式2（2020春•哈尔滨期末）如图，点A为∠MON的平分线上一点，过A任意作一条直线分别与∠MON的两边相交于B、C，P为BC中点，过P作BC的垂线交射线OA于点D，若∠MON＝115°，则∠BDC的度数为　 　度．【解答】解：如图：过D作DE⊥OM于E，DF⊥ON于F，则∠DEB＝∠DFC＝∠DFO＝90°，∵∠MON＝115°，∴∠EDF＝360°﹣90°﹣90°﹣115°＝65°，∵DE⊥OM，DF⊥ON，OD∠MON，∴DE＝DF，∵P为BC中点，DP⊥BC，∴BD＝CD，在Rt△DEB和Rt△DFC中，∴Rt△DEB ≌Rt△DFC（HL），∴∠EDB＝∠CDF，∴∠BDC＝∠BDF+CDF＝∠BDF+∠EDB＝∠EDF＝65°．故答案为：65．5性质1 等腰三角形的两个底角相等（等边对等角）.性质2 等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合（通常说成等腰三角形的“三线合一”）.等腰三角形的性质等腰三角形的性质和判定 ∴ AC=AB. ( )即△ABC为等腰三角形.∵∠B=∠C， ( )等腰三角形的判定方法如果一个三角形有两个角相等,那么这个三角形是等腰三角形（简写成“等角对等边”）.已知等角对等边 在△ABC中， 应用格式：((例5（2019秋•宜城市期末）如图，△ABC中，BO平分∠ABC，CO平分∠ACB，M，N经过点O，且MN∥BC，若AB＝5，△AMN的周长等于12，则AC的长为（　　）A．7 B．6 C．5 D．4【解答】解：∵BO平分∠CBA，CO平分∠ACB，∴∠MBO＝∠OBC，∠OCN＝∠OCB，∵MN∥BC，∴∠MOB＝∠OBC，∠NOC＝∠OCB，∴∠MBO＝∠MOB，∠NOC＝∠NCO，∴MO＝MB，NO＝NC，∵AB＝5，△AMN的周长等于12，∴△AMN的周长＝AM+MN+AN＝AB+AC＝5+AC＝12，∴AC＝7，故选：A．变式1（2020•青山区校级模拟）如图，在△ABC中，ED∥BC，∠ABC和∠ACB的平分线分别交ED于点G、F，若BE＝6，DC＝8，DE＝20，求FG．【解答】解：∵ED∥BC，∴∠EGB＝∠GBC，∠DFC＝∠FCB，∵∠GBC＝∠GBE，∠FCB＝∠FCD，∴∠EGB＝∠EBG，∠DCF＝∠DFC，∴BE＝EG，CD＝DF，∵BE＝6，DC＝8，DE＝20，∴FG＝DE﹣EG﹣DF＝DE﹣BE﹣CD＝20﹣6﹣8＝6．变式2（2019秋•潮南区期中）在△ABC中，BD是∠ABC的平分线，AD⊥BD，垂足是D．（1）求证：∠2＝∠1+∠C；（2）若ED∥BC，∠ABD＝28°，求∠ADE的度数．【解答】解：（1）如图延长AD交BC于H．∵BD⊥AH，∴∠BDA＝∠BDH＝90°，∵∠ABD＝∠HBD，BD＝BD，∴△BDA≌△BDH（ASA），∴BA＝BH，∠2＝∠BHA，∵∠BHA＝∠1+∠C，∴∠2＝∠1+∠C． （2）∵∠ABD＝28°，∠BDA＝90°，∴∠2＝62°，∴∠AHB＝∠2＝62°，∴∠AHC＝180°﹣62°＝118°，∵DE∥EC，∴∠ADE＝∠AHC＝118°．6等边三角形的性质和判定每一边上的中线、高和这一边所对的角的平分线互相重合三个角都相等，对称轴（3条）等边三角形对称轴（1条）两个底角相等底边上的中线、高和顶角的平分线互相重合且都是60º两条边相等三条边都相等三个角都相等的三角形是等边三角形，等边三角形从角看：两个角相等的三角形是等腰三角形从边看：两条边相等的三角形是等腰三角形三条边都相等的三角形是等边三角形小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”，你同意吗？等边三角形的判定方法： 有一个角是60°的等腰三角形是等边三角形.∵AB＝AC，∠A＝60°，∴△ABC是等边三角形，∴∠ACB＝60°，∵EC＝CD，∴∠CED＝∠CDE＝ ∠ACB＝30°，∴∠AEF＝30°，∴∠AFE＝90°，即EF⊥AB，∵△ABC是等边三角形，AE＝CE，∴BE平分∠ABC，∴EG＝EF＝2，在Rt△DEG中，DE＝2EG＝4，∴DF＝EF+DE＝2+4＝6；例6（2019秋•龙岩期末）如图，AB＝AC，AE＝EC＝CD，∠A＝60°，若EF＝2，则DF＝（　　）A．3 B．4 C．5 D．6【解答】解：如图，过点E作EG⊥BC，交BC于点G变式1（2018秋•和平区期中）下列说法：①等边三角形的三个内角都相等；②等边三角形的每一个角都等于60°；③三个角都相等的三角形是等边三角形；④有一个角是60°的等腰三角形是等边三角形．其中，正确说法的个数是（　　）A．1 B．2 C．3 D．4【解答】解：①等边三角形的三个内角都相等；正确；②等边三角形的每一个角都等于60°；正确；③三个角都相等的三角形是等边三角形；正确；④有一个角是60°的等腰三角形是等边三角形．正确；故选：D．7含30度角的直角三角形例7含有30°角的直角三角形，短直角边是斜边的一半（2020春•新邵县期末）如图，在△ABC中，∠C＝90°，AC＝2，∠B＝30°，点P是BC边上一动点，连接AP，则AP的长度不可能是（　　）A．2 B．3 C．4 D．5【解答】解：根据垂线段最短，可知AP的长不可小于2；∵△ABC中，∠C＝90°，AC＝2，∠B＝30°，∴AB＝4，∴AP的长不能大于4，故选：D．（2020春•北镇市期中）如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，CD是斜边AB上的高，若AD＝3cm，则斜边AB的长为（　　）变式1A．3cm B．6cm C．9cm D．12cm【解答】解：∵CD是斜边AB上的高，∴∠ADC＝90°，∵∠A＝60°，∠ACB＝90°，∴∠B＝180°﹣∠ACB﹣∠A＝30°，∠ACD＝180°﹣∠ADC﹣∠A＝30°，∵AD＝3cm，∴AC＝2AD＝6cm，∴AB＝2AC＝12cm，故选：D．8直角三角形斜边上中线例8直角三角形斜边上中线等于斜边的一半（2020•高州市模拟）如图，△ABC中，∠A+∠B＝90°，AD＝DB，CD＝3，则AB的长度为（　　）A．3 B．4 C．5 D．6【解答】解：∵△ABC中，∠A+∠B＝90°，∴∠ACB＝90°．∵AD＝DB，∴CD是该直角三角形斜边AB上的中线，∴AB＝2CD＝6．故选：D．变式1（2020春•包河区期末）如图，已知△ABC中，∠ACB＝90°，O为AB的中点，点E在BC上，且CE＝AC，∠BAE＝15°，则∠COE＝　　度． 轴对称与轴对称图形定义性质逆向应用确定对称轴等腰三角形与等边三角形性质判定应用最广泛的性质“三线合一”重要模型角平分线+垂线=等腰三角形角平分线+平行线=等腰三角形角的平分线的性质定理角的平分线的判定定理证明两条线段相等证明角相等辅助线添加方法