





还剩23页未读,
继续阅读
第2章轴对称图形复习 课件PPT
展开
这是一份第2章轴对称图形复习 课件PPT,共31页。
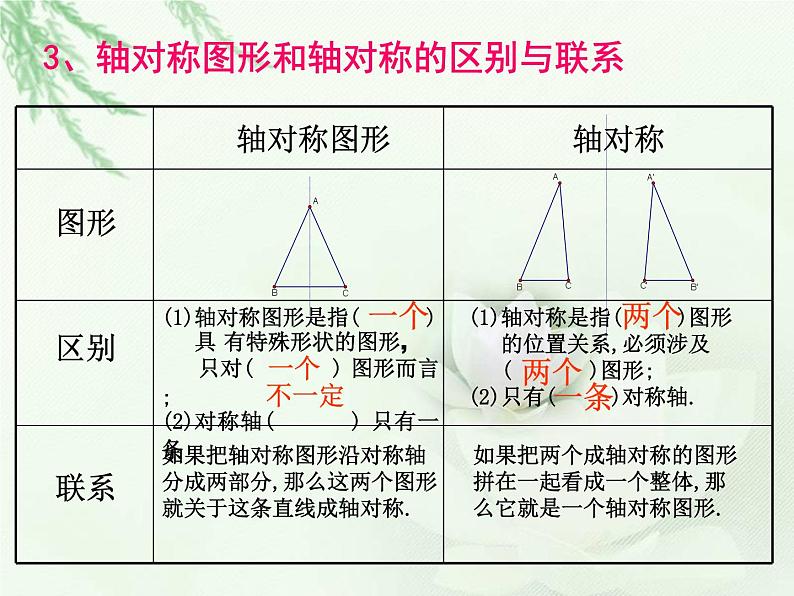
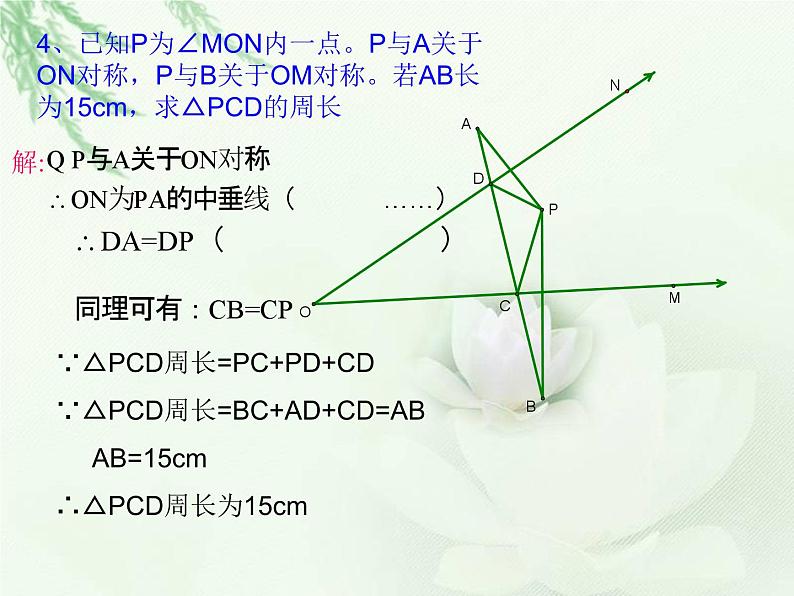
轴对称 把一个图形沿着某一条直线翻折,如果它能够与 重合,那么称这两个图形关于这条直线对称。也称这两个图形成 。这条直线叫做 。折叠后重合的点是对应点,也叫_______. 把一个图形沿着 折叠,如果它能够与另一个图形______,那么称这个图形就叫做 。这条直线就是它的 。 一.轴对称图形2、轴对称图形:1、轴对称:某一条直线重合轴对称图形对称点另一个图形对称轴轴对称对称轴3、轴对称图形和轴对称的区别与联系 轴对称图形轴对称 区别联系图形 (1)轴对称图形是指( ) 具 有特殊形状的图形, 只对( ) 图形而言;(2)对称轴( ) 只有一条(1)轴对称是指( )图形 的位置关系,必须涉及 ( )图形;(2)只有( )对称轴.如果把轴对称图形沿对称轴 分成两部分,那么这两个图形 就关于这条直线成轴对称.如果把两个成轴对称的图形 拼在一起看成一个整体,那么它就是一个轴对称图形.一个一个不一定两个两个一条(1)成轴对称的两个图形 . (2)如果两个图形成轴对称,那么对称轴是对称点连线的 .(1).轴对称的性质: (2).轴对称图形对称点的连线 。 互相平行或在同一条直线上 (3).轴对称图形中的对应线段所在直线:全等 (1)、平行 (2)、相交 (3)、共线(在同一条直线上) .4、轴对称的性质:垂直平分线练习:1、国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是( )A.加拿大、韩国、乌拉圭 B.加拿大、瑞典、澳大利亚C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士 加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士C2、小明照镜子的时候,发现T恤上的英文单词在镜子中呈现“ ”的样子,请你判断这个英文单词是( )(A)(B)(C)(D)A1、下列图形中,不是轴对称图形的是( ) A 角 B 线段 C 任两边都不相等的三角形 D 等边三角形2、下列图形中,只有一条对称轴的是( )ABCD3、点P(1,-2)关于y轴对称点的坐标是 ________CC(-1,-2)解:4、已知P为∠MON内一点。P与A关于ON对称,P与B关于OM对称。若AB长为15cm,求△PCD的周长∵△PCD周长=PC+PD+CD∵△PCD周长=BC+AD+CD=AB AB=15cm∴△PCD周长为15cm1、什么叫线段垂直平分线? 垂直并且平分一条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。2、线段垂直平分线性质1? 线段垂直平分线上的点到线段两端的距离相等。你能画图说明吗?二.线段的垂直平分线 到线段两端距离相等的点 在线段的垂直平分线上。4.线段垂直平分线的集合定义: 线段垂直平分线是到线段两端距离相等的所有点的集合。3、线段垂直平分线性质2? 如图,△ABC中,边AB、BC的垂直平分线交于点P。(1)求证:PA=PB=PC。(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。三、角的平分线的定理1: 角平分线上的点到角两边的距离相等.能否用三角形全等证明这个性质?角平分线性质的描述: ∵OC平分∠AOB上 PD⊥OA,PE⊥OB. ∴PD=PE.角的平分线的定理2: 角的内部到角两边距离相等的点在角的平分线上.能否用三角形全等证明这个性质? 如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB,BC,AC的距离相等.┌E┕DF┎思考:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系? 已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。解:点A(-3,5),B(-4,1),C(-1,3),关于y轴对称点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.····AB’A’C’ 归纳:先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.x y 四.用坐标表示轴对称小结: 在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点(x, y)关于x轴对称的点的坐标为______.点(x, y)关于y轴对称的点的坐标为______.(x, - y)(- x, y)五.利用轴对称变换作图1: 如图:要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道什么地方,可使所用的输气管道线最短?ABLP 有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。ABC利用轴对称变换作图2: 例1 、某中学七(4)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短? 作法:1.作点C关于直线 OA 的 对称点点D, 2. 作点C关于直线 OB 的对称点点E, 3.连接DE分别交直线OA.OB于点M.N, 则CM+MN+CN最短AOBC. .EDMNGH例2. 如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线,作法:1.作点C关于直线 OA 的 对称点点F, 2. 作点D关于直线 OB 的对称点点E, 3.连接EF分别交直线OA.OB于点G.H,则CG+GH+DH最短FAOBD ·· CEGH1、完成下表.(-2, -3)(2, 3)(-1,-2)(1, 2)(6, -5)(-6, 5)(0, -1.6)(0,1.6)(-4,0)(4,0)2、已知点P(2a+b,-3a)与点P’(8,b+2).若点p与点p’关于x轴对称,则a=_____ b=_______.若点p与点p’关于y轴对称,则a=_____ b=_______.246-20(抢答)3.如下图△ABC中,AC=16cm,DE为AB的垂直平分线, △BCE的周长为26cm,求BC的长。C三.(等腰三角形)知识点回顾1.等腰三角形的性质①.等腰三角形的两个底角相等。(等边对等角)②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(三线合一)2、等腰三角形的判定: 如果一个三角形有两个角相等,那么这两个角所对的边也相等。(等角对等边) 如图,在△ABC中,AB=AC时,(1)∵AD⊥BC∴∠ ____= ∠_____;____=____(2) ∵AD是中线∴____⊥____; ∠_____= ∠_____(3) ∵ AD是角平分线∵____ ⊥____;_____=____BADCADBDCDADBCBADCADADBCBDCD四.(等边三角形)知识点回顾1.等边三角形的性质: (1) 等边三角形的三个角都相等,并且每一个角都等于600 。 (2)等边三角形任一内角的平分线、与对边上的中线、对边上的高互相重合。(三线合一)2、等边三角形的判定: (1)三条边都相等的三角形是等边三角形。 (2)三个角都相等的三角形是等边三角形。 (3)有一个角是600的等腰三角形是等边三角形。 五.(直角三角形)知识点回顾1.直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半。(2)在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半。2、直角三角形的判定: (1)从角上考虑 (2)从边上考虑 1、“有一个等腰三角形的两条边长分别是4cm和8cm,则周长为 20cm2、若等腰三角形的一个角为400,则另外两个角的度数为700,700 或 400,10003、已知,如图: AB=AC ,AD=DC=BC 则∠A=3604、如图,已知:在△ABC中,∠BAC=90°,E为BC的中点,BD平分∠ABC,DE⊥BC于E,证明:∠C = 30°
轴对称 把一个图形沿着某一条直线翻折,如果它能够与 重合,那么称这两个图形关于这条直线对称。也称这两个图形成 。这条直线叫做 。折叠后重合的点是对应点,也叫_______. 把一个图形沿着 折叠,如果它能够与另一个图形______,那么称这个图形就叫做 。这条直线就是它的 。 一.轴对称图形2、轴对称图形:1、轴对称:某一条直线重合轴对称图形对称点另一个图形对称轴轴对称对称轴3、轴对称图形和轴对称的区别与联系 轴对称图形轴对称 区别联系图形 (1)轴对称图形是指( ) 具 有特殊形状的图形, 只对( ) 图形而言;(2)对称轴( ) 只有一条(1)轴对称是指( )图形 的位置关系,必须涉及 ( )图形;(2)只有( )对称轴.如果把轴对称图形沿对称轴 分成两部分,那么这两个图形 就关于这条直线成轴对称.如果把两个成轴对称的图形 拼在一起看成一个整体,那么它就是一个轴对称图形.一个一个不一定两个两个一条(1)成轴对称的两个图形 . (2)如果两个图形成轴对称,那么对称轴是对称点连线的 .(1).轴对称的性质: (2).轴对称图形对称点的连线 。 互相平行或在同一条直线上 (3).轴对称图形中的对应线段所在直线:全等 (1)、平行 (2)、相交 (3)、共线(在同一条直线上) .4、轴对称的性质:垂直平分线练习:1、国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是( )A.加拿大、韩国、乌拉圭 B.加拿大、瑞典、澳大利亚C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士 加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士C2、小明照镜子的时候,发现T恤上的英文单词在镜子中呈现“ ”的样子,请你判断这个英文单词是( )(A)(B)(C)(D)A1、下列图形中,不是轴对称图形的是( ) A 角 B 线段 C 任两边都不相等的三角形 D 等边三角形2、下列图形中,只有一条对称轴的是( )ABCD3、点P(1,-2)关于y轴对称点的坐标是 ________CC(-1,-2)解:4、已知P为∠MON内一点。P与A关于ON对称,P与B关于OM对称。若AB长为15cm,求△PCD的周长∵△PCD周长=PC+PD+CD∵△PCD周长=BC+AD+CD=AB AB=15cm∴△PCD周长为15cm1、什么叫线段垂直平分线? 垂直并且平分一条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。2、线段垂直平分线性质1? 线段垂直平分线上的点到线段两端的距离相等。你能画图说明吗?二.线段的垂直平分线 到线段两端距离相等的点 在线段的垂直平分线上。4.线段垂直平分线的集合定义: 线段垂直平分线是到线段两端距离相等的所有点的集合。3、线段垂直平分线性质2? 如图,△ABC中,边AB、BC的垂直平分线交于点P。(1)求证:PA=PB=PC。(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。三、角的平分线的定理1: 角平分线上的点到角两边的距离相等.能否用三角形全等证明这个性质?角平分线性质的描述: ∵OC平分∠AOB上 PD⊥OA,PE⊥OB. ∴PD=PE.角的平分线的定理2: 角的内部到角两边距离相等的点在角的平分线上.能否用三角形全等证明这个性质? 如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB,BC,AC的距离相等.┌E┕DF┎思考:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系? 已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。解:点A(-3,5),B(-4,1),C(-1,3),关于y轴对称点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.····AB’A’C’ 归纳:先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.x y 四.用坐标表示轴对称小结: 在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点(x, y)关于x轴对称的点的坐标为______.点(x, y)关于y轴对称的点的坐标为______.(x, - y)(- x, y)五.利用轴对称变换作图1: 如图:要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道什么地方,可使所用的输气管道线最短?ABLP 有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。ABC利用轴对称变换作图2: 例1 、某中学七(4)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短? 作法:1.作点C关于直线 OA 的 对称点点D, 2. 作点C关于直线 OB 的对称点点E, 3.连接DE分别交直线OA.OB于点M.N, 则CM+MN+CN最短AOBC. .EDMNGH例2. 如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线,作法:1.作点C关于直线 OA 的 对称点点F, 2. 作点D关于直线 OB 的对称点点E, 3.连接EF分别交直线OA.OB于点G.H,则CG+GH+DH最短FAOBD ·· CEGH1、完成下表.(-2, -3)(2, 3)(-1,-2)(1, 2)(6, -5)(-6, 5)(0, -1.6)(0,1.6)(-4,0)(4,0)2、已知点P(2a+b,-3a)与点P’(8,b+2).若点p与点p’关于x轴对称,则a=_____ b=_______.若点p与点p’关于y轴对称,则a=_____ b=_______.246-20(抢答)3.如下图△ABC中,AC=16cm,DE为AB的垂直平分线, △BCE的周长为26cm,求BC的长。C三.(等腰三角形)知识点回顾1.等腰三角形的性质①.等腰三角形的两个底角相等。(等边对等角)②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(三线合一)2、等腰三角形的判定: 如果一个三角形有两个角相等,那么这两个角所对的边也相等。(等角对等边) 如图,在△ABC中,AB=AC时,(1)∵AD⊥BC∴∠ ____= ∠_____;____=____(2) ∵AD是中线∴____⊥____; ∠_____= ∠_____(3) ∵ AD是角平分线∵____ ⊥____;_____=____BADCADBDCDADBCBADCADADBCBDCD四.(等边三角形)知识点回顾1.等边三角形的性质: (1) 等边三角形的三个角都相等,并且每一个角都等于600 。 (2)等边三角形任一内角的平分线、与对边上的中线、对边上的高互相重合。(三线合一)2、等边三角形的判定: (1)三条边都相等的三角形是等边三角形。 (2)三个角都相等的三角形是等边三角形。 (3)有一个角是600的等腰三角形是等边三角形。 五.(直角三角形)知识点回顾1.直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半。(2)在直角三角形中,如果一个锐角等于300,那么它所对的直角边等于斜边的一半。2、直角三角形的判定: (1)从角上考虑 (2)从边上考虑 1、“有一个等腰三角形的两条边长分别是4cm和8cm,则周长为 20cm2、若等腰三角形的一个角为400,则另外两个角的度数为700,700 或 400,10003、已知,如图: AB=AC ,AD=DC=BC 则∠A=3604、如图,已知:在△ABC中,∠BAC=90°,E为BC的中点,BD平分∠ABC,DE⊥BC于E,证明:∠C = 30°
相关资料
更多









