第二章轴对称图形2.4线段角的轴对称性3教案(苏科版八上)
展开2.4线段、角的轴对称性(2)
教学目标
【知识与能力】
探索并掌握角平分线的性质定理和逆定理; 2.能利用所学知识提出问题并能解决生活中的实际问题。
【过程与方法】
能利用基本事实有条理的进行证明,做到每一步有根有据。
【情感态度价值观】
经历探索角的轴对称的过程,在“操作——探究——归纳——证明”的过程中培养思考的严谨性和表达的条理性.
教学重难点
【教学重点】
利用角的轴对称性探索角平分线的性质.
【教学难点】
理解“点在角平分线上”的证明方法.
课前准备
无
教学过程
教学过程: 教师活动 | 学生活动 | 设计意图 |
开场白 同学们,上节课我们充分研究了线段的轴对称性,那么另一个基本图形“角”的轴对称性又如何呢?与线段有什么异同和联系呢?下面,我们就进入今天愉快的数学探究之旅. | 进入状态,兴致盎然,跃跃欲试. | 点明课题,揭示角类比线段的探究方法. |
实践探索一 在一张薄纸上画∠AOB,它是轴对称图形吗?如果是,对称轴在哪里?为什么? | 积极思考,动手操作,提出猜想. | 让学生动手操作,感知角的轴对称性,猜想对称轴的位置,为后续研究作铺垫,同时激发学生的学习兴趣. |
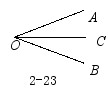
实践探索二 如图2-23,直线OC是∠AOB的角平分线,如果沿直线OC翻折,你有什么发现?角平分线是线段的对称轴吗?
]
| 动手操作,验证猜想,描述发现,明确结论. | 在操作中感知角的轴对称性,培养口头表达能力. |
实践探索三 角平分线是否也有像线段垂直平分线一样的特殊性质呢? 如图,在∠AOB的角平分线OC任意取一点P,PD⊥OA,PE⊥OB,PD与PE相等吗?为什么? 通过证明,你发现了什么?用语言描述你得到的结论.
总结 角平分线上的点有什么特点? | 学生独立思考、积极探究.方法不一,具体如下: 1.利用“AAS”证明△ODP≌ △OEP后,说明PD与PE相等. 2.利用角的轴对称性和基本事 实“过一点有且只有一条直线与已知直线垂直”,说明PD与PE相等. | 问题虽然比较简单,学生都能感受到PD与PE相等,但是要让学生进行推理说明还是有困难的,要提示学生从角平分线的定义入手,说明角相等,再结合证明两个角相等的思路,让学生寻找到演绎推理的过程,培养学生的动手能力和探索精神,为下面的证明积累经验. |
实践探索四 如果任意一个点在角平分线上,那么这个点到这个角的两边距离相等.反过来,结合上节课所学,你有什么猜想?
通过上述探索,你得到了什么结论? 教师利用几何画板验证. | 1. 猜想角平分线性质定理的逆定理. 2.学生证明逆定理. 连接OQ,利用HL证明三角形全等,继而得到OQ平分∠AOB. 3.学生讨论、归纳得到角平分线性质定理的逆定理:角的内部到角两边距离相等的点在角的平分线上.. | 教师提示问题,帮助学生利用类比学习法合猜想,培养学生的逆向思维能力. 逆定理的证明,通过引导学生理解“点在线上”的证法基础上,明确辅助线,培养其分析问题和演绎推理的能力. 让学生感受角平分线点的共性,几何画板的一般性图形验证,较好地进行了图形证明. |
小结 1.经历了画图、折纸、猜想、归纳的活动过程,探索得到了角的轴对称性:角是轴对称图形,对称轴是角平分线所在的直线. 2.本节课我们还证明了角平分线的性质定理:角平分线上的点到角的两边的距离相等;反过来,角的内部到角的两边距离相等的点在角的平分线上,从中我们可以发现图形的位置关系与数量关系的内在联系,你能举例说明这种内在的联系吗? | 学生讨论、小结 | 帮助学生及时归纳所学,纳入原有知识体系中. |
布置作业 课本P58习题2.4,分析第7、8题的思路,任选1题写出过程. | 学生根据自身实际情况,选题作业. | 实行作业分层,便于不同发展水平的学生自我发展. |