第7章《复数全章复习》课件+分层练习（基础+提升，含答案解析）

这是一份第7章《复数全章复习》课件+分层练习（基础+提升，含答案解析），文件包含第7章《复数全章复习》课件人教版高中数学必修二pptx、第7章《复数全章复习单元测试》分层练习基础+提升含答案解析docx等2份课件配套教学资源，其中PPT共36页， 欢迎下载使用。

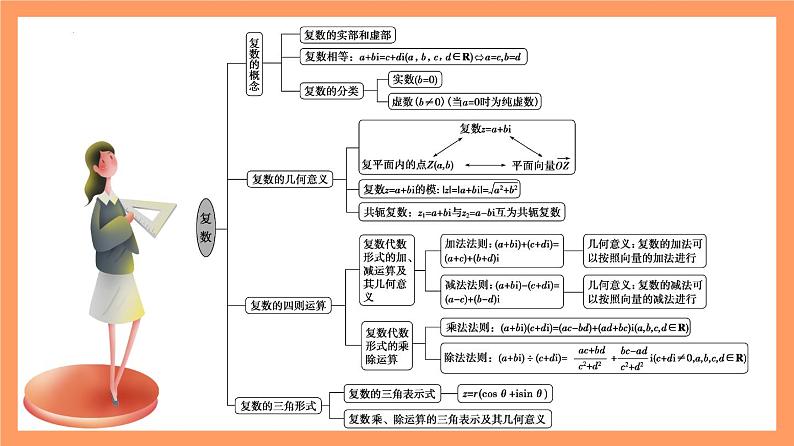
第7章复数全章复习人教版高中数学必修二(1)通过方程的解，认识复数引入的表现，理解复数的代数表示；(2)理解复数的分类，掌握复数相等的充要条件；(3)了解复平面的概念,理解复数的几何意义；(4)掌握复数的模、共轭复数的概念，会求复数的模和一个复数的共轭复数；(5)能熟练进行复数代数形式的加减乘除运算，了解加减法的几何意义；1.数系扩充自然数集N整数集Z引入负数(负号)引入分数(分数线)有理数集Q引入无理数(根号)实数集R自然数整数有理数实数引入虚数i复数集复数2.复数的相关概念(1)复数集C={a+bi|a,b∈R}(2)复数z=a+bi(a,b∈R)(3)虚数单位i：规定i2=﹣1；i的幂有周期性，周期为4.2.复数的相关概念(4)复数相等：作用：将复数问题转化为实数问题．注：①若两个复数能比较大小，则它们必为实数.②一般对两个不全是实数的复数只能说相等或不相等，不能比较大小.如：3与1+2i不能比较大小；2+3i与1+2i不能比较大小.2.复数的相关概念(5)复数的几何意义：①建立了直角坐标系来表示复数的平面叫复平面； x轴叫实轴，y轴叫虚轴.②实轴上的点都表示实数(b=0)；③虚轴上的点(除原点外)都表示纯虚数(a=0,b≠0)；2.复数的相关概念(6)复数的模：(7)共轭复数：实部相等，虚部互为相反数的两个复数叫做共轭复数.2.复数的相关概念(8)实系数一元二次方程在复数集内的解3.复数的四则运算(1)复数加法与减法的运算法则：实部和虚部分别相加/减设z1＝a＋bi，z2＝c＋di是任意两个复数，则z1＋z2＝ ，z1－z2＝ ___.(a＋c)＋(b＋d)i(a－c)＋(b－d)i对任意z1，z2，z3∈C，有加法交换律：z1＋z2＝z2＋z1， 加法结合律：(z1＋z2)＋z3＝z1＋(z2＋z3)(2)复数加法与减法的几何意义：对应向量相加/减复数差的模=对应向量差的模=两点距离3.复数的四则运算(3)复数乘法的运算法则：类似于多项式的乘法设z1＝a＋bi，z2＝c＋di是任意两个复数，则z1z2＝(a＋bi)(c＋di)＝ac＋bci＋adi＋bdi2＝(ac－bd)＋(ad＋bc)i对于任意z1，z2，z3∈C，有①乘法交换律：z1·z2＝z2·z1②乘法结合律：(z1·z2)·z3＝z1·(z2·z3)③乘法对加法的分配律：z1(z2＋z3)＝z1z2＋z1z3(4)复数除法的运算法则：分母实数化(上下同乘分母的共轭复数)一、复数的有关概念例1　当实数a为何值时，z＝a2－2a＋(a2－3a＋2)i.(1)为实数；解　由z∈R，得a2－3a＋2＝0，解得a＝1或a＝2.(2)为纯虚数；(3)对应的点在第一象限内；解　依题得(a2－2a)－(a2－3a＋2)＝0，∴a＝2.(4)复数z对应的点在直线x－y＝0上.∴a的取值范围是(－∞，0)∪(2，＋∞).(1)复数的概念主要包括复数的代数形式、复数的分类、复数相等、共轭复数及复数的模等知识点，其中，复数的分类及复数的相等是热点，复数分类中“纯虚数”的条件是难点和易错点.(2)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题，只需把复数化为代数形式，列出实部、虚部满足的方程(不等式)即可.解　设z＝x＋yi(x，y∈R)，∵z＋2i＝x＋(y＋2)i为实数，∴y＝－2.∴z＝4－2i.∵(z＋ai)2＝(12＋4a－a2)＋8(a－2)i，∴实数a的取值范围是(2,6).(1)复数z＝a＋bi(a，b∈R)同复平面上的点Z(a，b)是一一对应的，同向量 是一一对应的.(3)复数加减法的几何意义实质上是向量加减法的三角形法则和平行四边形法则，由减法的几何意义可知|z1－z2|表示复平面上两点Z1，Z2之间的距离.＝i＋(－i)1 009＋0＝0.(1)复数的除法运算是复数运算中的难点，如果遇到(a＋bi)÷(c＋di)的形式，首先应该写成分式的形式，然后再分母实数化.(2)虚数单位i的周期性①i4n＋1＝i，i4n＋2＝－1，i4n＋3＝－i，i4n＝1(n∈N*)；②in＋in＋1＋in＋2＋in＋3＝0(n∈N*).【思想方法解读】数形结合既是一种重要的数学思想，又是一种常用的数学方法．本章中，复数本身的几何意义、复数的模以及复数加减法的几何意义都是数形结合思想的体现．它们的这种意义架起了联系复数与解析几何、平面几何的桥梁，使得复数问题和几何问题得以相互转化．涉及的主要问题有复数在复平面内对应点的位置、复数运算、点的轨迹及模的最值问题等．例4.已知|z|＝1.(1)求|z－(2＋2i)|的最值；(2)求|z－i|·|z＋1|的最大值．【点评】掌握常见的复平面上的点的轨迹方程的复数表示方式，灵活运用模的几何意义及复数运算的几何意义，通过数形结合，充分利用图形的直观、形象的特点，可简化对问题的处理．【思想方法解读】分类讨论是一种重要的逻辑方法，也是一种常用的数学思想，在高考中占有十分重要的地位．该思想在本章的很多知识中都有体现，常见的有：对复数分类的讨论、复数对应点的轨迹的讨论、一元二次方程根的讨论等．(1)是实数；(2)是虚数；(3)是纯虚数；(4)是0.例5.实数k分别为何值时，复数(1＋i)k2－(3＋5i)k－2(2＋3i)满足下列条件？【点评】遇到题目中含有参数的复数问题，常常结合参数对结果的影响进行分类讨论．【思想方法解读】复数相等的充要条件是把复数问题转化为实数问题的重要依据，是复数问题实数化这一重要数学思想的体现．把复数问题实数化处理，主要根据复数相等建立方程或方程组，通过解方程或方程组，达到解题的目的．两式相加，整理得a2＋6a＋8＝0，解得a1＝－2，a2＝－4，对应得b1＝－1，b2＝2.∴所求实数为a＝－2，b＝－1或a＝－4，b＝2.【点评】复数问题化归为实数问题，是解决复数问题的一种重要思想方法． 1.(2020年新课标Ⅱ)(1－i)4＝ (　　)A．－4 B．4C．－4i D．4i【答案】A【解析】(1－i)2＝－2i，(1－i)4＝－4.故选A．【点评】本题考查复数的运算性质，是基础的计算题．【答案】D【点评】本题考查复数模的求法，考查数学转化思想方法，是基础题．【答案】D【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．解析：课程结束人教A版2019必修第二册