高中数学人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积试讲课课件ppt

这是一份高中数学人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积试讲课课件ppt，文件包含831《棱柱棱锥棱台的表面积和体积》课件人教版高中数学必修二pptx、831《棱柱棱锥棱台的表面积和体积》分层练习基础+提升含答案解析docx等2份课件配套教学资源，其中PPT共35页， 欢迎下载使用。

1.通过对棱柱、棱锥、棱台的研究，掌握棱柱、棱锥、棱台的表面积和体积的求法．2.会求与棱柱、棱锥、棱台有关的组合体的表面积和体积．
前面我们分别认识了基本立体图形的结构特征和平面表示，本节进一步认识简单几何体的表面积和体积，它表示几何体表面的大小，体积是几何体所占空间的大小.
多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
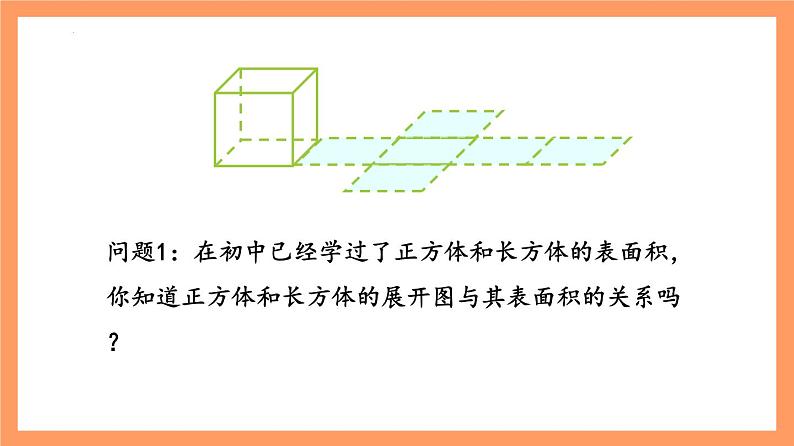
问题1：在初中已经学过了正方体和长方体的表面积，你知道正方体和长方体的展开图与其表面积的关系吗？
问题2：多面体的展开图与其表面积的关系？
多面体的表面积就是围成多面体各个面的面积的和，也就是展开图的面积。
（1）直棱柱的侧面展开图是什么？如何计算它的表面积？
正棱柱的侧面展开图是一个长方形
（2）斜棱柱的侧面积为多少？如何计算它的表面积？
（3）棱锥的侧面展开图是什么？如何计算它的表面积？
（4）正棱锥的侧面展开图是什么？如何计算它的表面积？
侧面展开图是全等的三角形
（5）正棱台的侧面展开图是什么？如何计算它的表面积？
（1）棱柱、棱锥、棱台的侧面展开图分别是由若干个平行四边形、若干个三角形、若干个梯形组成的平面图形，侧面展开图的面积就是棱柱、棱锥、棱台的侧面积.
（2）棱柱、棱锥、棱台的表面积等于它们的侧面积与各自的底面积的和.
例1 如图示，四面体P-ABC各棱长均为a，求它的表面积.
解：∵∆ABC是正三角形，其边长为a.
因此，四面体P-ABC的表面积为
又∵四面体P-ABC各棱长均为a，
∴四面体四个都是正三角形，
例2 如右图，一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m，公共面ABCD是边长为1m的正方形，那么这个漏斗的容积是多少立方米?
1. 正六棱台的上，下底面边长分别是2cm和6cm，侧棱长是5cm，求它的表面积.
解：如图示，AB=6cm，A′B′=2cm，AA′=5cm.
因此，正六棱台的表面积为
2. 如图是一个表面被涂上红色的棱长是4cm的立方体，将其适当分割成棱长为1cm的小立方体. (1) 共得到多少个棱长为1cm的小立方体？ (2) 三面是红色的小立方体有多少个？它们的表面积之和是多少？ (3) 两面是红色的小立方体有多少个？它们的表面积之和是多少？ (4) 一面是红色的小立方体有多少个？它们的表面积之和是多少？ (5) 六面均没有颜色的小立方体有多少个？它们的表面积之和是多少？它们占有多少立方厘米的空间？
(1) 共有64个棱长为1cm的小立方体.
(2) 三面是红色的小立方体有8个, 表面积之和是48cm2.
3. 某广场设置了一些石凳供大家休息，这些石凳是由正方体截去八个一样的四面体得到的. 如果被截正方体的棱长是50cm，那么石凳的体积是多少？
如图示，由题意知正方体的棱长为0.5m，则有
4. 求证：直三棱柱的任意两个侧面的面积和大于第三个侧面的面积.
如图示，直三棱柱ABC-A′B′C′中，设底面ABC的三边分别为a,b,c，棱柱的高为h，则有
∴直三棱柱的任意两个侧面的面积和大于第三个侧面的面积.
1、三棱锥P-ABC中，PA⊥底面ABC，PA=3.底面ABC是边长为2的正三角形，则三棱锥P-ABC的体积等于_______
3、某几何体的三视图如图所示，则该几何体的表面积为(　　)A．54 B．60 C．66 D．72
1. 求几何体的表面积
通常将所给几何体分成基本几何体，再通过这些基本几何体的表面积进行求和或作差，从而获得几何体的表面积，另外有时也会用到将几何体展开求其展开图的面积进而得表面积．
2. 求几何体体积的常用方法