





还剩13页未读,
继续阅读
4.3.2 用坐标表示平移 浙教版数学八年级上册课件
展开
这是一份4.3.2 用坐标表示平移 浙教版数学八年级上册课件,共21页。
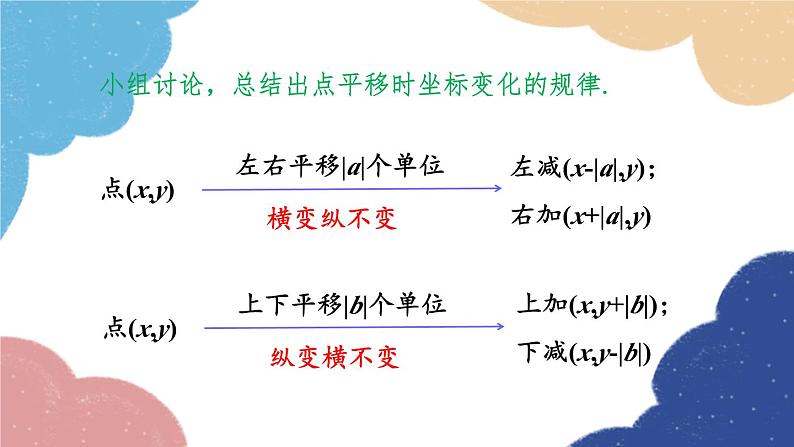
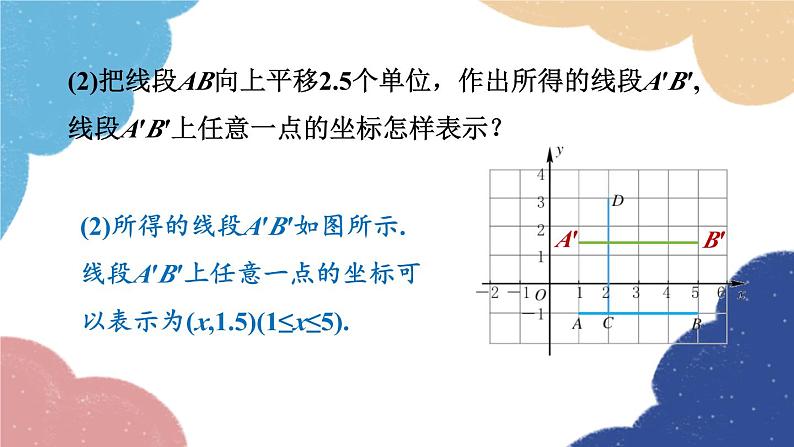
4.3 坐标平面内图形的 轴对称和平移第2课时 用坐标表示平移学习目标1.了解当坐标平面内图形左、右或上、下平移时对应点之间的坐标关系.2.会求已知点左、右或上、下平移后所得的对应点的坐标.3.会利用平移(左、右或上、下)后对应点之间的坐标关系,分析已知图形的平移.合作学习 如图,将点A(-3,3),B(4,5)分别作以下平移,作出相应的点,并写出点的坐标.A(-3,3)向右平移5个单位(2,3)B(4,5)向左平移5个单位( )-1,5A(-3,3)向上平移5个单位( )-3,8B(4,5)向下平移5个单位( )4,0 比较各点平移时的坐标变化,填在表格内.你能发现点平移时坐标变化的规律吗?合作学习A(-3,3)向右平移5个单位(2,3)B(4,5)向左平移5个单位( )-1,5A(-3,3)向上平移5个单位( )-3,8B(4,5)向下平移5个单位( )4,0坐标变化减5不变不变加5不变减5小组讨论,总结出点平移时坐标变化的规律.点(x,y)左右平移|a|个单位横变纵不变左减(x-|a|,y);右加(x+|a|,y)点(x,y)上下平移|b|个单位纵变横不变上加(x,y+|b|);下减(x,y-|b|)例题讲解例1 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5,则线段AB上任意一点的坐标都可以用“(x,-1) (1≤x≤5)”表示.按照类似这样的规定,回答下面的问题:(1)怎样表示线段CD上任意一点的坐标?解:(1)线段CD上任意一点的坐标可表示为(2,y)(-1≤y≤3).(2)把线段AB向上平移2.5个单位,作出所得的线段A′B′,线段A′B′上任意一点的坐标怎样表示?A′B′(2)所得的线段A′B′如图所示.线段A′B′上任意一点的坐标可以表示为(x,1.5)(1≤x≤5).(3)把线段CD向左平移3个单位,作出所得的线段C′D′.线段C′D′上任意一点的坐标怎样表示?(3)所得的线段C′D′如图所示.线段C′D′上任意一点的坐标可以表示为(-1,y)(-1≤y≤3).C′D′例2 如图.(1)分别求出点A,A′和点B,B′的坐标,并比较A与A′,B与B′之间的坐标变化.解:(1)点A,A′坐标分别为A(-8,-1), A′(-3,4); 点B,B′坐标分别为B(-3,-1), B′(2,4).由A到A′,横坐标增加5,纵坐标增加5;由B到B′,横坐标增加5,纵坐标增加5.(2)图甲怎样平移得到图乙?(2)由第(1)题知,A,B都向右平移5个单位,向上平移5个单位.从图甲到图乙,可以看做经过了两次平移:一次是向右平移5个单位,另一次是向上平移5个单位.思考:从图甲到图乙,可以看做只经过一次平移得到吗? 思路拓展 例3 如图,在平面直角坐标系中,把△ABC进行平移,使点A移至原点O处.请画出平移后的△OB′C′,并求出△OB′C′三个顶点的坐标和平移的距离. C′B′方法总结坐标平面内的图形平移三步法(1)明确平移的方向和距离.(2)找出图形中的关键点.(3)利用平移规律确定平移后的各对应点的坐标,顺次连结各点得到平移后的图形.1.点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A.(-3,0)B.(-1,6)C.(-3,-6)D.(-1,0)随堂练习解析:点P(-2,-3)向左平移1个单位,得到(-3,-3);(-3,-3)向上平移3个单位,得到(-3,0).A2.如图,在平面直角坐标系中,点A的坐标为(1,3),将线段OA向左平移2个单位,得到线段O′A′,则点A的对应点A′的坐标为___________.解析:如图,根据方格结构找出线段OA向左平移2个单位后的对应点O′,A′的位置,连结O′,A′,得到线段O′A′,即可得A′的坐标为(-1,3).(-1,3)3.在平面直角坐标系中,△ABC的三个顶点的位置如图所示.(1)平移△ABC,使点C与坐标原点O是对应点,请直接写出A,B两点的对应点A′,B′的坐标,并画出平移后的△A′B′C′.解:(1)点A′,B′的坐标分别是(1,-3), (3,1), 如图所示:A′B′(C′)(2)△ABC是怎样平移得到△A′B′C′的?A′B′(C′)(2)△ABC平移得到△A′B′C′,可以看成经过了两次平移:一次是向左平移1个单位,一次是向下平移2个单位.(3)若△ABC内部一点P的坐标为(a,b),求平移后点P的对应点P′的坐标.A′B′(C′)(3)点P′的坐标是(a-1,b-2).课堂小结设点P的坐标为(x,y),则在平面直角坐标系中点P平移时坐标变化如下:点P(x,y)的平移方式(a>0,b>0)平移后点的坐标沿x轴平移沿y轴平移向右平移a个单位长度向左平移a个单位长度向上平移b个单位长度向下平移b个单位长度(x+a,y)(x-a,y)(x,y+b)(x,y-b)左减右加,上加下减感谢观看!
4.3 坐标平面内图形的 轴对称和平移第2课时 用坐标表示平移学习目标1.了解当坐标平面内图形左、右或上、下平移时对应点之间的坐标关系.2.会求已知点左、右或上、下平移后所得的对应点的坐标.3.会利用平移(左、右或上、下)后对应点之间的坐标关系,分析已知图形的平移.合作学习 如图,将点A(-3,3),B(4,5)分别作以下平移,作出相应的点,并写出点的坐标.A(-3,3)向右平移5个单位(2,3)B(4,5)向左平移5个单位( )-1,5A(-3,3)向上平移5个单位( )-3,8B(4,5)向下平移5个单位( )4,0 比较各点平移时的坐标变化,填在表格内.你能发现点平移时坐标变化的规律吗?合作学习A(-3,3)向右平移5个单位(2,3)B(4,5)向左平移5个单位( )-1,5A(-3,3)向上平移5个单位( )-3,8B(4,5)向下平移5个单位( )4,0坐标变化减5不变不变加5不变减5小组讨论,总结出点平移时坐标变化的规律.点(x,y)左右平移|a|个单位横变纵不变左减(x-|a|,y);右加(x+|a|,y)点(x,y)上下平移|b|个单位纵变横不变上加(x,y+|b|);下减(x,y-|b|)例题讲解例1 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5,则线段AB上任意一点的坐标都可以用“(x,-1) (1≤x≤5)”表示.按照类似这样的规定,回答下面的问题:(1)怎样表示线段CD上任意一点的坐标?解:(1)线段CD上任意一点的坐标可表示为(2,y)(-1≤y≤3).(2)把线段AB向上平移2.5个单位,作出所得的线段A′B′,线段A′B′上任意一点的坐标怎样表示?A′B′(2)所得的线段A′B′如图所示.线段A′B′上任意一点的坐标可以表示为(x,1.5)(1≤x≤5).(3)把线段CD向左平移3个单位,作出所得的线段C′D′.线段C′D′上任意一点的坐标怎样表示?(3)所得的线段C′D′如图所示.线段C′D′上任意一点的坐标可以表示为(-1,y)(-1≤y≤3).C′D′例2 如图.(1)分别求出点A,A′和点B,B′的坐标,并比较A与A′,B与B′之间的坐标变化.解:(1)点A,A′坐标分别为A(-8,-1), A′(-3,4); 点B,B′坐标分别为B(-3,-1), B′(2,4).由A到A′,横坐标增加5,纵坐标增加5;由B到B′,横坐标增加5,纵坐标增加5.(2)图甲怎样平移得到图乙?(2)由第(1)题知,A,B都向右平移5个单位,向上平移5个单位.从图甲到图乙,可以看做经过了两次平移:一次是向右平移5个单位,另一次是向上平移5个单位.思考:从图甲到图乙,可以看做只经过一次平移得到吗? 思路拓展 例3 如图,在平面直角坐标系中,把△ABC进行平移,使点A移至原点O处.请画出平移后的△OB′C′,并求出△OB′C′三个顶点的坐标和平移的距离. C′B′方法总结坐标平面内的图形平移三步法(1)明确平移的方向和距离.(2)找出图形中的关键点.(3)利用平移规律确定平移后的各对应点的坐标,顺次连结各点得到平移后的图形.1.点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A.(-3,0)B.(-1,6)C.(-3,-6)D.(-1,0)随堂练习解析:点P(-2,-3)向左平移1个单位,得到(-3,-3);(-3,-3)向上平移3个单位,得到(-3,0).A2.如图,在平面直角坐标系中,点A的坐标为(1,3),将线段OA向左平移2个单位,得到线段O′A′,则点A的对应点A′的坐标为___________.解析:如图,根据方格结构找出线段OA向左平移2个单位后的对应点O′,A′的位置,连结O′,A′,得到线段O′A′,即可得A′的坐标为(-1,3).(-1,3)3.在平面直角坐标系中,△ABC的三个顶点的位置如图所示.(1)平移△ABC,使点C与坐标原点O是对应点,请直接写出A,B两点的对应点A′,B′的坐标,并画出平移后的△A′B′C′.解:(1)点A′,B′的坐标分别是(1,-3), (3,1), 如图所示:A′B′(C′)(2)△ABC是怎样平移得到△A′B′C′的?A′B′(C′)(2)△ABC平移得到△A′B′C′,可以看成经过了两次平移:一次是向左平移1个单位,一次是向下平移2个单位.(3)若△ABC内部一点P的坐标为(a,b),求平移后点P的对应点P′的坐标.A′B′(C′)(3)点P′的坐标是(a-1,b-2).课堂小结设点P的坐标为(x,y),则在平面直角坐标系中点P平移时坐标变化如下:点P(x,y)的平移方式(a>0,b>0)平移后点的坐标沿x轴平移沿y轴平移向右平移a个单位长度向左平移a个单位长度向上平移b个单位长度向下平移b个单位长度(x+a,y)(x-a,y)(x,y+b)(x,y-b)左减右加,上加下减感谢观看!
相关资料
更多









