2021学年4.3 坐标平面内图形的轴对称和平移教课内容课件ppt

这是一份2021学年4.3 坐标平面内图形的轴对称和平移教课内容课件ppt，共12页。PPT课件主要包含了－3－2，－2－3等内容，欢迎下载使用。

第一课时 用坐标表示轴对称
1．(3分)如图，在平面直角坐标系xOy中，点P(－3，5)关于y轴的对称点的坐标为(　　)A．(－3，－5)　　　　　　B．(3，5)C．(3，－5) D．(5，－3)
2．(3分)点P(－2，3)关于x轴对称的点的坐标是(　　)A．(－3，2) B．(2，－3)C．(－2，－3) D．(2，3)
3．(3分)平面直角坐标系中，点P的坐标为(－5，3)，则点P关于y轴的对称点的坐标是(　　)A．(5，3) B．(－5，－3)C．(3，－5) D．(－3，5)4．(3分)下列语句：①点A(5，－3)关于x轴对称的点A′的坐标为(－5，－3)；②点B(－2，2)关于y轴对称的点B′的坐标为(－2，－2)；③若点D在第二、四象限坐标轴夹角平分线上，则点D的横坐标与纵坐标相等. 其中正确的是(　　)A．① B．② C．③ D．①②③都不正确
5．(8分)(1)点P(－3，2)关于x轴对称的点P′的坐标是 ．(2)点(2，－3)关于y轴对称的点的坐标是 .(3)若点(a，－4)与点(－3，b)关于x轴对称，则a＝ ，b＝ ．(4)若点(a，－4)与点(－3，b)关于y轴对称，则a＝ ，b＝ ．6．(4分)如图，△ABC的顶点都在正方形网格格点上，点A的坐标为(－1，4)．将△ABC沿y轴翻折到第一象限，则点C的对应点C′的坐标是 ．7．(4分)已知点P1(a－1，4)和点P2(2，b)关于x轴对称，则(a＋b)2 015＝ ．
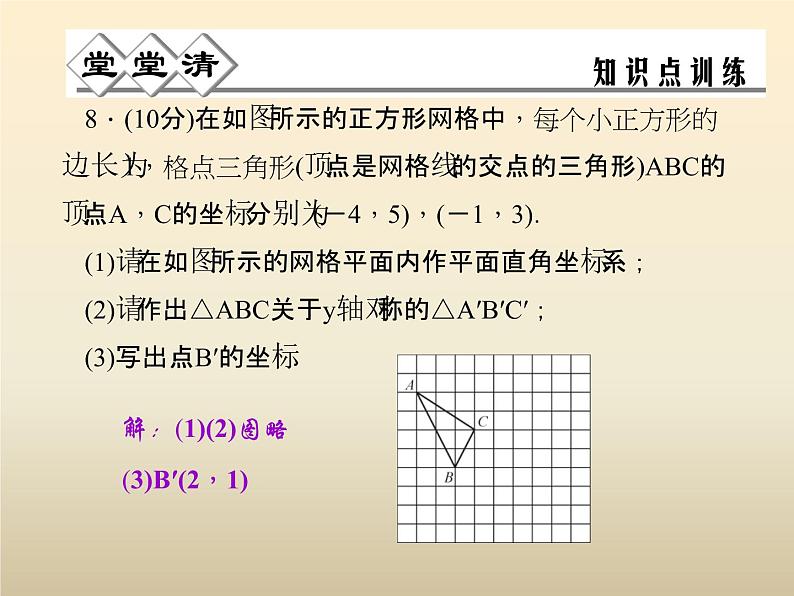
8．(10分)在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形(顶点是网格线的交点的三角形)ABC的顶点A，C的坐标分别为(－4，5)，(－1，3)．(1)请在如图所示的网格平面内作平面直角坐标系；(2)请作出△ABC关于y轴对称的△A′B′C′；(3)写出点B′的坐标．
解：(1)(2)图略(3)B′(2，1)
9．(12分)如图，在平面直角坐标系xOy中，已知点A(－1，5)，B(－1，0)，C(－4，3)．(1)求出△ABC的面积；(2)在图中作出△ABC关于y轴的对称图形△A1B1C1；(3)写出点A1，B1，C1的坐标．
10．(6分)已知点P(a＋1，2a－3)关于x轴的对称点在第一象限，则a的取值范围是(　　)
11．(6分)甲、乙两位同学用围棋子做游戏．如图所示，现轮到黑棋下子，黑棋下子后白棋再下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也组成轴对称图形．则下列下子方法不正确的是[说明：棋子的位置用数对表示，如A点在(6，3)](　　)
A．黑(3，7)，白(5，3) B．黑(4，7)，白(6，2)C．黑(2，7)，白(5，3) D．黑(3，7)，白(2，6)
12．(6分)如图，平面直角坐标系中有四个点，它们的横、纵坐标均为整数．若在此平面直角坐标系内移动点A，使得这四个点构成的四边形是轴对称图形，并且点A的横坐标仍是整数，则移动后点A的坐标为 ．
(－1，1)或(－2，－2)或(0，2)或(－2，－3)
13．(16分)如图所示，在长方形ABCD中，已知点A(－8，2)，B(0，2)，C(0，6)．求：(1)点D的坐标；(2)点A到x轴的距离；(3)作出长方形ABCD关于y轴对称的图形A′B′C′D′，并求出A′，B′，C′，D′四点的坐标及点A与点D′之间的距离．
14．(8分)如图，一束光线从y轴上点A(0，2)出发，经过x轴上点C反射后经过点B(6，6)，则光线从点A到点B所经过的路程是(　　)A．10　　　B．8　　　C．6　　　D．4