青岛版数学八年级上册 5.5三角形内角和定理第2课时直角三角形的内角和课件

这是一份青岛版数学八年级上册 5.5三角形内角和定理第2课时直角三角形的内角和课件，共11页。

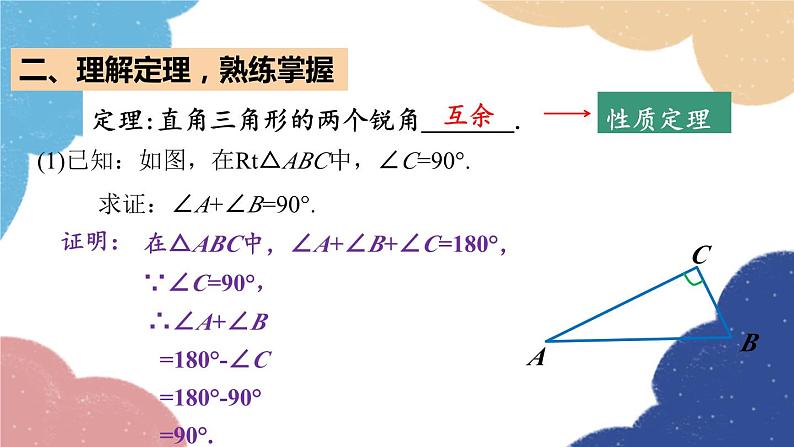
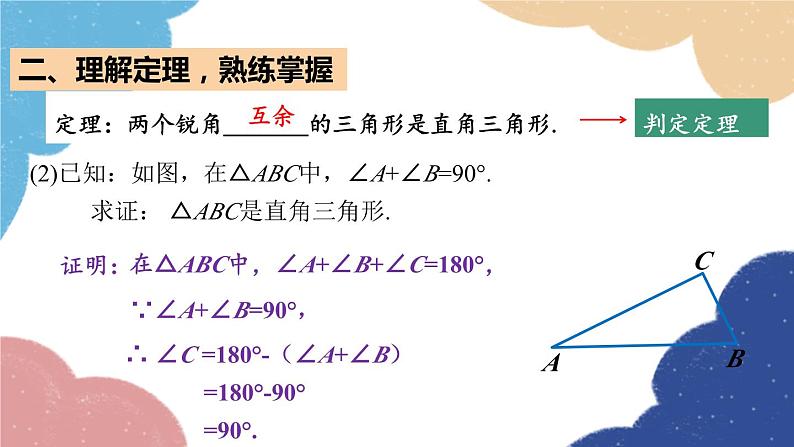
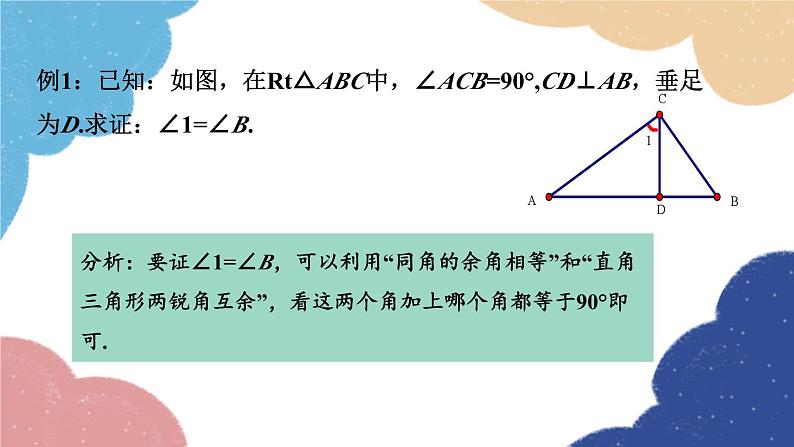
5.5三角形内角和定理第2课时 直角三角形的内角和一、认真思考，回答问题想一想(1)直角三角形的两个锐角有怎样的关系？(2)如果一个三角形有两个锐角互余，那么这个三角形是 直角三角形吗？答：两个锐角的和为90°，即两个锐角互余.答：是直角三角形.定理:直角三角形的两个锐角_______.(1)已知：如图，在Rt△ABC中，∠C=90°. 求证：∠A+∠B=90°.ACB证明：在△ABC中，∠A+∠B+∠C=180°，∵∠C=90°，∴∠A+∠B =180°-∠C =180°-90° =90°.互余二、理解定理，熟练掌握性质定理定理：两个锐角_______的三角形是直角三角形.(2)已知：如图，在△ABC中，∠A+∠B=90°. 求证： △ABC是直角三角形.ACB证明：在△ABC中，∠A+∠B+∠C=180°，∵∠A+∠B=90°，∴ ∠C =180°-（∠A+∠B） =180°-90° =90°.互余二、理解定理，熟练掌握判定定理例1：已知：如图，在Rt△ABC中，∠ACB=90°,CD⊥AB，垂足为D.求证：∠1=∠B.分析：要证∠1=∠B，可以利用“同角的余角相等”和“直角三角形两锐角互余”，看这两个角加上哪个角都等于90°即可. 例1：已知：如图，在Rt△ABC中，∠ACB=90°,CD⊥AB，垂足为D.求证：∠1=∠B.证明：在Rt△ABC中，∵ ∠ACB=90°(已知),∴ ∠B+ ∠A=90°(直角三角形的两个锐角互余), 在△ADC中， ∵ CD⊥AB(已知)，∴ ∠ADC=90°(垂直的定义)，∴ △ADC是直角三角形(直角三角形的定义)，∴ ∠1+ ∠A=90°(直角三角形的两个锐角互余)，∴ ∠1=∠B(等量代换).三、互相交流，探索规律性质定理：直角三角形的两个锐角互余.判定定理：有两个锐角互余的三角形是直角三角形.观察下列定理，它们的条件和结论之间有怎样的关系？ 条件：直角三角形 结论：两锐角互余条件:两锐角互余 结论:直角三角形四、巩固练习，能力提升1.下列三角形是直角三角形，请写出对应角的度数.15°75°20°33°32°40°57°68°58°50°70°22°2.判断下列三角形哪些是直角三角形.25°25°60°33°32°70°57°68°58°30°60°22°3.已知：如图，在△ABC中，AD⊥BC，∠1=∠B.求证：△ABC是直角三角形.证明：∵AD⊥BC(已知)，∴∠ADC=90°(垂直的定义).∴△ACD是直角三角形(直角三角形的定义).∴∠1+∠C=90°(直角三角形的两个锐角互余).∵ ∠1=∠B(已知)，∴∠B+∠C=90°(等量代换).∴△ABC是直角三角形(两个锐角互余的三角形是直角三角形).直角三角形性质定理：直角三角形判定定理：课堂小结直角三角形的两个锐角互余;两个锐角互余的三角形是直角三角形.