


初中数学青岛版八年级上册5.6 几何证明举例背景图课件ppt
展开我们曾利用角的轴对称性质,通过实验的方法,探索出角平分线的性质:
角平分线上的点,到这个角的两边的距离相等.
你能用推理的方法证明它的真实性吗?
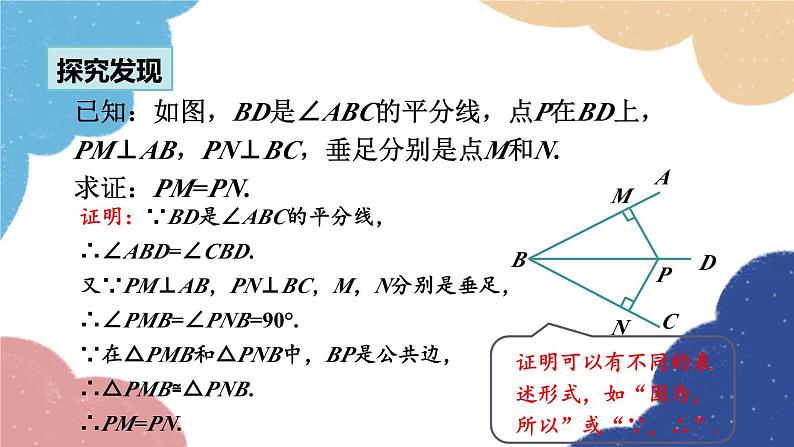
已知:如图,BD是∠ABC的平分线,点P在BD上,PM⊥AB,PN⊥BC,垂足分别是点M和N.求证:PM=PN.
证明:∵BD是∠ABC的平分线,∴∠ABD=∠CBD.又∵PM⊥AB,PN⊥BC,M,N分别是垂足,∴∠PMB=∠PNB=90°.∵在△PMB和△PNB中,BP是公共边,∴△PMB≌△PNB.∴PM=PN.
证明可以有不同的表述形式,如“因为,所以”或“∵,∴”.
角平分线的性质定理:角平分线上的点到这个角的两边的距离相等.
你能说出角平分线的性质定理的逆命题吗?
角的内部到角的两边距离相等的点在这个角的平分线上.
它的逆命题正确吗?如果你认为正确,能加以证明吗?
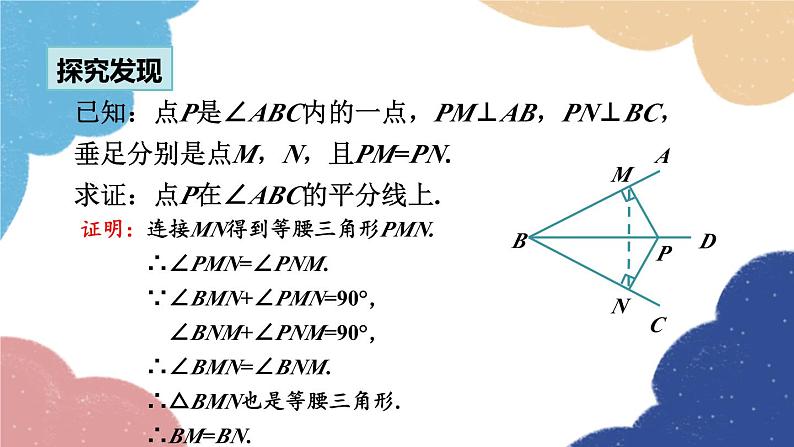
证明:连接MN得到等腰三角形PMN. ∴∠PMN=∠PNM. ∵∠BMN+∠PMN=90°, ∠BNM+∠PNM=90°, ∴∠BMN=∠BNM. ∴△BMN也是等腰三角形. ∴BM=BN.
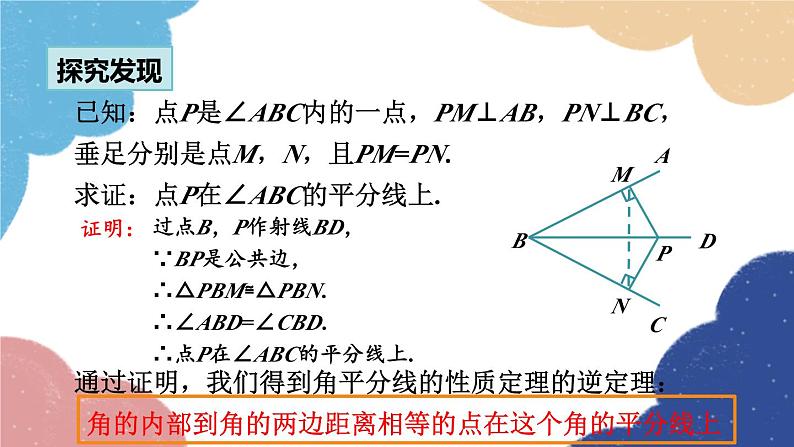
已知:点P是∠ABC内的一点,PM⊥AB,PN⊥BC,垂足分别是点M,N,且PM=PN.求证:点P在∠ABC的平分线上.
过点B,P作射线BD,∵BP是公共边,∴△PBM≌△PBN.∴∠ABD=∠CBD.∴点P在∠ABC的平分线上.
通过证明,我们得到角平分线的性质定理的逆定理:
已知:如图,AP,CP分别是△ABC的外角∠MAC,∠NCA的平分线,AP,CP相交于点P,过点P作PD⊥BM,垂足为点D,作PF⊥BN,垂足为点F,连接BP.求证:BP是∠ABC的平分线.
证明:如图所示,过点P作PE⊥AC,垂足为点E. ∵AP,CP分别平分∠MAC,∠NCA, 且PD⊥BM,PF⊥BN, ∴PD=PE,PF=PE. ∴PD=PF.
又∵PD⊥BM,PF⊥BN, ∴点P在∠ABC的平分线上. ∴BP是∠ABC的平分线.
证明一条射线是一个角的平分线时,一般过这条射线上的一点作角两边的垂线,证明这两条垂线段相等.
已知:如图,AM,BN,CP是△ABC的三条角平分线.求证:AM,BN,CP交于一点.
要证明三角形的三条角平分线交于一点,只要证明两条角平分线的交点也在第三条角平分线上就可以了.
证明:如图,设AM,BN交于点O.过点O分别作OD⊥BC,OE⊥AC,OF⊥AB,垂足分别为点D,E,F.∵O是∠BAC角平分线AM上的一点,∴OE=OF.同理,OD=OF.∴OD=OE.∵CP是∠ACB的平分线,∴O在CP上.因此,AM,BN,CP交于一点.
三角形三条角平分线交于一点.
1.如图,已知BE⊥AC,CF⊥AB,点E,F为垂足,D是BE与CF的交点, AD平分∠BAC.求证: BD=CD.
证明:∵AD平分∠BAC,BE⊥AC,CF⊥AB(已知),∴DF=DE(角平分线上的点到这个角度两边的距离相等).又∵∠DFB=∠DEC=90°(垂直的定义),∠FDB=∠DEC(对顶角相等),∴△DFB≌△DEC(ASA),∴BD=CD(全等三角形的对应边相等).
2.如图,在Rt△ABC中,∠C=90°,AC=BC.AD是∠A的平分线.求证: AB=AC+CD.
证明:如图所示,过点D作DE⊥AB于点E.∵AD平分∠CAB,∴CD=DE,∠CAD=∠EAD.∵AC=BC,∴∠CAB=∠B.∵∠CAB+∠B=90°,∴∠B=45°.∵∠EDB+∠B=90°,∴∠EDB=∠B=45°,∴DE=BE,CD=BE.
∵∠CAD=∠EAD,∠C=∠AED,AD=AD,∴△ACD≌△AED.∴AC=AE.∵AB=AE+BE,∴AB=AC+CD.
初中数学青岛版八年级上册5.6 几何证明举例图文ppt课件: 这是一份初中数学青岛版八年级上册5.6 几何证明举例图文ppt课件,共16页。PPT课件主要包含了教学目标,新知导入,探究新知,课堂练习,课堂小结等内容,欢迎下载使用。
初中青岛版2.6 等腰三角形教学演示课件ppt: 这是一份初中青岛版2.6 等腰三角形教学演示课件ppt,共20页。PPT课件主要包含了温故知新,探究发现,还有其他的证法吗,等边对等角,BDDC,三线合一,方法探究,作辅助线,构造全等三角形,对应边相等等内容,欢迎下载使用。
初中数学青岛版八年级上册2.5 角平分线的性质教案配套课件ppt: 这是一份初中数学青岛版八年级上册2.5 角平分线的性质教案配套课件ppt,共17页。PPT课件主要包含了学习目标,活动探究,轴对称,所以PDPE,同理PEPF,随堂练习,所以FGFM,所以FMFH,所以FGFH等内容,欢迎下载使用。













