青岛版八年级数学上册5.5 三角形内角和定理（2） 教学课件

这是一份青岛版八年级数学上册5.5 三角形内角和定理（2） 教学课件，共14页。

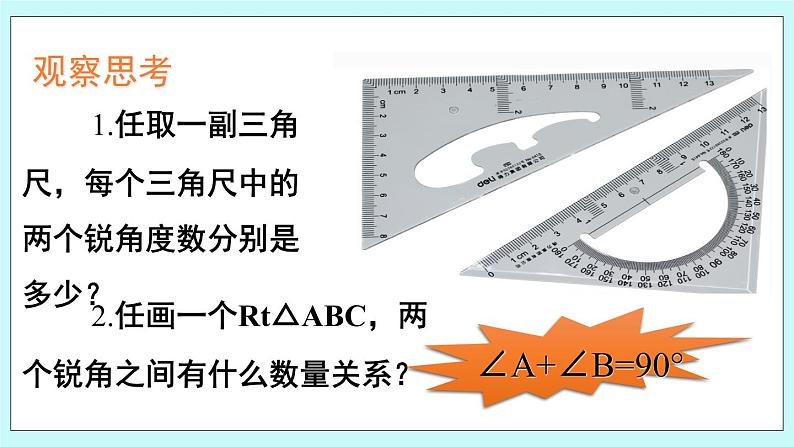
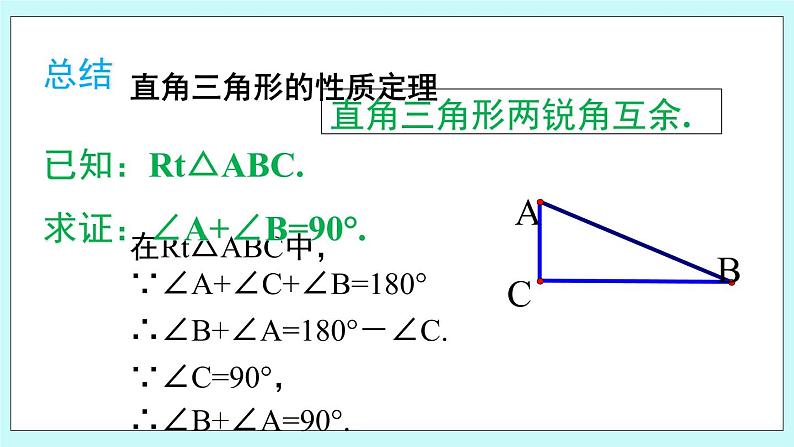
5.5 三角形内角和定理（2）青岛版数学八年级上册 1.掌握直角三角形的性质定理和它的判定定理； 2.会用直角三角形的性质定理和它的判定定理进行推理.1.三角形内角和定理是什么？2.三角形内角和定理的推论是什么？3.什么是互余？4.几何命题的证明步骤有哪些？观察思考 1.任取一副三角尺，每个三角尺中的两个锐角度数分别是多少？ 2.任画一个Rt△ABC，两个锐角之间有什么数量关系？总结直角三角形的性质定理直角三角形两锐角互余.在Rt△ABC中，∵∠A+∠C+∠B=180°∴∠B+∠A=180°－∠C.∵∠C=90°，∴∠B+∠A=90°.已知：Rt△ABC.求证：∠A+∠B=90°.思考探究两锐角互余的三角形是直角三角形吗？ 直角三角形性质定理的逆命题是什么？真or假已知：在△ABC中， ∠A＋∠B ＝ 90゜. 求证：△ABC是直角三角形.在△ABC中，∵∠A+∠C+∠B=180°∴∠B+∠A=180°－∠C.∴180°－∠C=90°，∵∠B+∠A=90°，∴∠C=90°.直角三角形的判定定理两锐角互余的三角形是直角三角形. 例1. 已知：如图，在Rt△ABC中，∠ACB=90°,CD⊥AB，垂足为D. 求证：∠1=∠B证明 在Rt△ABC中，∵∠ACB=90°( ),∴∠B+∠A=90°( ).在△ADC中，∵CD⊥AB( ),∴∠ADC=90°( ).已知直角三角形两锐角互余垂直的定义已知 例1. 已知：如图，在Rt△ABC中，∠ACB=90°,CD⊥AB，垂足为D. 求证：∠1=∠B∴∠A+∠1=90°( ).∴∠1=∠B ( ).∴△ADC是直角三角形( ).(接上页)直角三角形的定义直角三角形两锐角互余等量代换 1.如图，在△ABC中，∠B=∠C,D是BC边的一点。过D作DF⊥BC，DE⊥AB，垂足分别为点F,E。求证：∠FDE=∠C。 2.如图，已知△ABC中,已知∠B＝65°,∠C＝45°, AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数。直角三角形性质定理： 直角三角形两锐角互余;直角三角形判定定理： 有两个锐角互余的三角形是直角三角形.作业课本173页练习：1，2题；课本174页练习：5,6,7题.