




初中数学华师大版八年级上册第12章 整式的乘除12.5 因式分解完美版课件ppt
展开1.理解因式分解的意义和概念及其与整式乘法的区别和联系.(重点)2.理解并掌握提公因式法并能熟练地运用提公因式法分解因式.(难点)
运用前面所学的知识填空:(1) m(a + b + c) = ; (2) (x + 1)(x - 1) = ;(3) (a + b)2 = .
ma + mb + mc
a2 + 2ab + b2
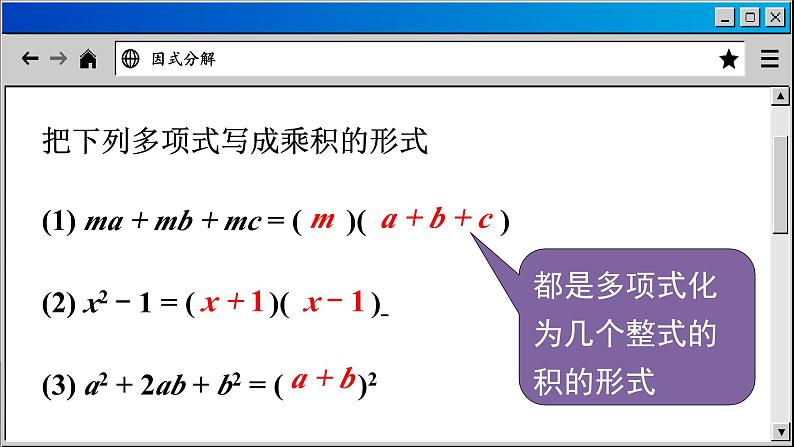
把下列多项式写成乘积的形式(1) ma + mb + mc = ( )( )(2) x2 - 1 = ( )( ) (3) a2 + 2ab + b2 = ( )2
都是多项式化为几个整式的积的形式
m a + b + c
x + 1 x - 1
定义:把一个多项式化为几个整式的积的形式,叫做多项式因式分解,也叫做这个多项式分解因式.
想一想:整式乘法与因式分解有什么关系?
x2 - 1 (x + 1)(x - 1)
x2 - 1 = (x + 1)(x - 1)等式的特征:左边是多项式,右边是几个整式的乘积
在下列等式中,从左到右的变形属于因式分解的有______________;不是因式分解的,请说明为什么.
① am + bm + c = m(a + b) + c② 24x2y = 3x ·8xy③(2x + 1)2 = 4x2 + 4x + 1④x2- 1 = (x + 1)(x- 1)⑤x2 + x = x2(1 + )⑥2x + 4y + 6z = 2(x + 2y + 3z)
因式分解的对象是多项式
这个多项式有什么特点?
pa + pb + pc
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
因式分解之基本方法 — 提公因式法
如何确定一个多项式的公因式?
找 3 x 2 – 6 xy 的公因式.
指数:相同字母的最低次数
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a + b + c )
正确找出多项式各项公因式的关键是:1.定系数:公因式的系数是多项式各项系数的最大公约数. 2.定字母: 字母取多项式各项中都含有的相同的字母. 3.定指数:相同字母的指数取各项中最小的一个,即字母最低次幂.
找一找:下列各多项式的公因式是什么?(1) 3x + 6y (2) ab - 2ac(3) a2 - a3 (4) 9m2n - 6mn (5) - 6x2y - 8xy2
(1) 8a3b2 + 12ab3c;
例2 把下列各式分解因式:
分析:提公因式法的步骤 (分两步): 第一步:找出公因式; 第二步:提取公因式,即将多项式化为两个因式的乘积.
(2) 2a(b + c) - 3(b + c).
整体思想是数学中一种重要而且常用的思想方法.
解:(1) 8a3b2 + 12ab3c= 4ab2 · 2a2 + 4ab2 · 3bc= 4ab2(2a2 + 3bc).
如果提出公因式4ab,另一个因式是否还有公式?
另一个因式将是 2a2b + 3b2c,
(2)2a(b + c) - 3(b + c)= (b + c)(2a - 3).
如何检查因式分解是否正确?
做整式乘法运算去检验.
因式分解:(1)3a3c2+12ab3c;(2)2a(b+c)-3(b+c);(3)(a+b)(a-b)-a-b.
(3)原式=(a+b)(a-b-1).
解:(1)原式=3ac(a2c+4b3).
(2)原式=(2a-3)(b+c).
小明的解法有误吗?因式分解:12x2y + 18xy2.
解:原式 = 3xy(4x + 6y).
正确解:原式 = 6xy(2x + 3y).
小亮的解法有误吗?因式分解:3x2 - 6xy + x.
解:原式 = x(3x - 6y).
当多项式的某一项和公因式相同时,提公因式后剩余的项是 1.
注意:某项提出莫漏 1.
正确解:原式 = 3x · x - 6y · x + 1 · x = x(3x - 6y + 1)
小华的解法有误吗?因式分解:- x2 + xy - xz.
解:原式 = - x(x + y - z).
提出负号时括号里的项没变号
注意:首项有负常提负.
正确解:原式 = - (x2 - xy + xz) = - x(x - y + z).
1. 把下列各式分解因式:(1) 8m2n + 2mn =_____________;(2) 12xyz - 9x2y2 =_____________;(3) p(a2 + b2 ) - q(a2 + b2 ) =______________; (4) -x3y3 - x2y2 - xy =_______________;(5) (x - y)2 + y(y - x) =______________.
2mn(4m + 1)
3xy(4z - 3xy)
(a2 + b2)(p - q)
-xy(x2y2 + xy + 1)
(y - x)(2y - x)
2.分解因式:(x - y)2 + y(y - x).
解法1:(x - y)2 + y(y - x) = (x - y)2 - y(x - y) = (x - y)(x - y - y) = (x - y)(x - 2y).
解法2:(x - y)2 + y(y - x) = (y - x)2 - y(y - x) = (y - x)(y - x + y) = (y - x)(2y - x).
3. 简便计算:1.992 + 1.99 × 0.01= 1.99(1.99 + 0.01) = 3.98. (2) 20222 + 2022 – 20232= 2022×(2022 + 1) - 20232= 2022×2023 - 20232 = 2023×(2022 - 2023)= - 2023.
(3) (- 2)101 + (- 2)100.= (-2)100×(-2 + 1) = 2100×(- 1) = - 2100.
4. (1) 已知 2x + y = 4,xy = 3,求代数式 2x2y + xy2 的值;2x2y + xy2 = xy(2x + y) = 3×4 = 12.
(2) 化简求值:(2x + 1)2 - (2x + 1)(2x - 1),其中 x = .= (2x + 1)[(2x + 1) - (2x - 1)]= (2x + 1)(2x + 1 - 2x + 1) = 2(2x + 1).将 x = 代入上式,得原式 = 4.
1.认识平方差公式、完全平方公式的特点.(重点)2.会运用这两种公式将多项式分解因式.(难点)
1.什么叫多项式的因式分解?把一个多项式化成几个整式的积的形式,叫做多项式的因式分解.
2.下列式子从左到右哪个是因式分解?哪个是整式乘法?它们有什么关系?
1. a(x + y) = ax + ay 2. ax + ay = a(x + y)
它们是互为方向相反的变形
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
1.定系数:公因式的系数是多项式各项系数的最大公约数. 2.定字母: 字母取多项式各项中都含有的相同的字母. 3.定指数:相同字母的指数取各项中最小的一个,即字母最低次幂.
正确找出多项式各项公因式的关键是:
还记得前面学过的乘法公式吗?平方差公式:两数和(差)的平方公式:
a2 - b2 = (a + b)(a - b)
(a ± b)2 = a2 ±2ab + b2
运用平方差公式因式分解
想一想:多项式 a2 - b2 有什么特点?你能将它分解因式吗?
是 a,b 两数的平方差的形式
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
辨一辨:下列多项式能否用平方差公式来分解因式,为什么?
(1)x2 + y2(2)x2 - y2(3) - x2 - y2(4) - x2 + y2(5)x2 - 25y2(6)m2 - 1
- ( x2 + y2 )
( x + 5y )( x - 5y )
( m + 1 )( m - 1 )
( x + y )( x - y )
( y + x)( y - x )
= (2x+3)(2x-3).
方法总结:公式中的 a,b 无论表示数,单项式,还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
………… 一提(公因式)
解:(1)原式 = ( x2 )2 - ( y2 )2
= ( x2 + y2 )( x2 - y2 )
= ( x2 + y2 )( x - y )( x - y ).
三查(多项式的因式分解要分解到不能再分解为止)
两数和(或差)平方公式:两数和(或差)平方公式的特点:1.必须是三项式(或可以看成三项的)2.有两个同号的数或式的平方;3.中间有两底数之积的±2 倍.
运用两数和(或差)平方公式因式分解
凡具备这些特点的三项式,就是两数和(或差)平方公式,将它写成两数和(或差)平方形式,便实现了因式分解.
利用公式把某些具有特殊形式(如平方差式,两数和(或差)平方公式等)的多项式分解因式,这种分解因式的方法叫做公式法.
对照公式 a² ± 2ab + b² = (a ± b)² 进行因式分解,你会吗?1、x² + 4x + 4 = ( )² + 2·( )·( ) + ( )² = ( )²2、m² - 6m + 9 = ( )² - 2·( )·( ) + ( )² = ( )²
3、a² + 4ab + 4b² = ( )² + 2·( )·( ) + ( )² = ( )²
下列各式是不是两数和(或差)平方公式? (1)a2 - 6a + 9; (2)1 + 4a²; (3)4b2 + 4b - 1; (4)a2 + ab + b2; (5)x2 + x + 0.25.
分析:(2)因为它只有两项.(3)4b² 与 - 1 的符号不统一.(4)中间项缺 2 倍.
例3 分解因式:(1)16x2 + 24x + 9; (2)-x2 + 4xy - 4y2.
分析:(1)中,16x2 = (4x)2, 9 = 3²,24x = 2·4x·3, 所以 16x2 + 24x + 9 是一个两数和平方公式,即 16x2 + 24x + 9 = (4x)2 + 2×4x·3 + 32.
(2)中首项有负号,一般先利用添括号法则,将其变形为 -(x2 - 4xy+ 4y2),然后再利用公式分解因式.
例3 分解因式:(1)16x2 + 24x + 9; (2)-x2 + 4xy - 4y2.解: (1) 16x2 + 24x + 9 = ( 4x )2 + 2·4x·3 + ( 3 )2= ( 4x + 3 )2.
(2) -x2 + 4xy - 4y2 = -( x2 - 4xy + 4y2 )= -( x - 2y )2.
把下列各式分解因式:(1)3ax2 + 6axy + 3ay2;有公因式 3a,应先提出公因式,再进一步分解因式(2)(a+b)2 - 12(a + b) + 36.中将 a + b 看成一个整体,设 a + b = m,则原式化为 m2 - 12m + 36.
把下列各式分解因式:(1)3ax2 + 6axy + 3ay2;(2)(a+b)2 - 12(a + b) + 36.
例5 利用两数和(或差)平方公式简便计算:(1) 1002 - 2×100×99 + 99²; (2) 342 + 34×32 + 162.
1. 把下列各式分解因式:(1) 16a2 - 9b2 =__________________; (2) ( a + b )2 - ( a - b )2=________; (3) 9xy3 - 36x3y =____________________; (4) - a4 + 16 =_______________________.
( 4a + 3b )( 4a - 3b )
9xy( y + 2x )( y - 2x )
( 4 + a2 )( 2 + a )( 2 - a )
2.把下列多项式因式分解.(1)x2-12x + 36; (2)4a2-4a + 1;
= x2-2·x·6 + 62= (x-6)2.
= (2a)2-2·2a·1 + 12= (2a-1)2.
(3)y2 + 2y + 1 - x2 .
= (y + 1)² - x²= (y + 1 + x)(y + 1 - x).
3.多项式 4a² + ma + 9 是两数和(或差)平方公式,那么 m 的值是 .4. 若 ( 2x )n - 81 可分解成 ( 4x2 + 9 )( 2x + 3)( 2x - 3 ),则 n 的值是______.
5. 已知 4m + n = 40,2m - 3n = 5.求 (m + 2n)2 - (3m - n)2 的值.= (m + 2n + 3m - n)(m + 2n - 3m + n)= (4m + n)(3n - 2m)= -(4m + n)(2m - 3n).当 4m + n = 40,2m - 3n = 5 时,原式 = -40×5 = -200.
am + bm + mc = m(a + b + c)
确定公因式的方法:三定,即定系数;定字母;定指数
分两步:第一步找公因式;第二步提公因式
注意:①分解因式是一种恒等变形;②公因式:要提尽;③不要漏项;④提负号,要注意变号
平方差公式:a2-b2 = (a + b)(a - b)
一提:公因式;二套:公式;三查:多项式的因式分解有没有分解到不能再分解为止.
两数和(或差)平方公式:a2±2ab+b2 = (a±b)2
数学八年级上册12.5 因式分解示范课ppt课件: 这是一份数学八年级上册12.5 因式分解示范课ppt课件,共49页。PPT课件主要包含了今天你学到了什么,4因式分解⑴,同学们再见,第2课时,4因式分解,第3课时,第4课时,第5课时,第6课时等内容,欢迎下载使用。
华师大版八年级上册12.5 因式分解背景图ppt课件: 这是一份华师大版八年级上册12.5 因式分解背景图ppt课件,文件包含125因式分解pptx、习题125pptx、第1课时因式分解1doc、第2课时因式分解2doc等4份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
初中数学华师大版八年级上册12.5 因式分解课文课件ppt: 这是一份初中数学华师大版八年级上册12.5 因式分解课文课件ppt,文件包含125因式分解课件pptx、习题125课件ppt等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。













