

还剩52页未读,
继续阅读
所属成套资源:华师大版数学初二上学期PPT课件整册
成套系列资料,整套一键下载
华师大版数学八上13.2 三角形全等的判定(课件PPT)
展开
这是一份华师大版数学八上13.2 三角形全等的判定(课件PPT),共60页。
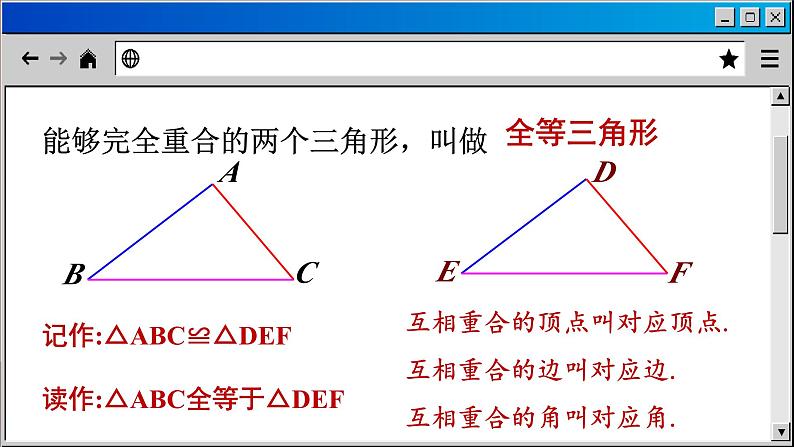
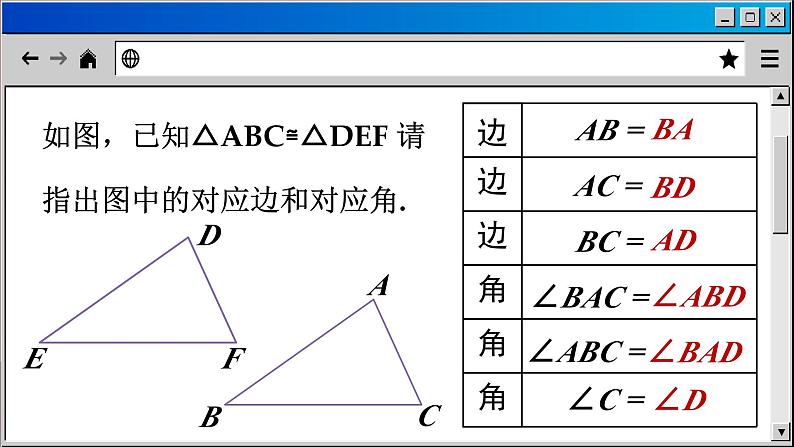
13.2 三角形全等的判断1. 全等三角形1.理解全等三角形的概念,及全等三角形经过一系列变换后,能够完全重合的性质.(重点)2. 掌握全等三角形的性质(对应边相等,对应角相等)和判定条件.(难点)学习目标复习导入全等图形:能够完全重合的两个图形叫做全等图形.全等形包括规则图形和不规则图形全等.能够完全重合的两个三角形,叫做全等三角形记作:△ABC≌△DEF读作:△ABC全等于△DEF互相重合的顶点叫对应顶点.互相重合的边叫对应边.互相重合的角叫对应角.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.如图,已知△ABC≌△DEF 请指出图中的对应边和对应角.∠D∠BAD∠ABDADBDBAAB =AC =BC =∠BAC =∠ABC =∠C =归纳有公共边的,公共边一般是对应边.全等三角形如图,以直线 l 为对称轴,画出△ABC 的对称图形,并指出它们的对应顶点、对应边和对应角.若已知∠A = 60°,∠B = 80°,那么△DEF 的各个角的大小:∠D = ,∠E = ,∠F = . 60°80°40°l一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等.AACBABDCDBCABCE2. 全等三角形的判定条件全等三角形的判定条件怎么判断两个三角形全等呢? 根据全等三角形的定义可知:能够完全重合两个三角形全等,即两个三角形的三对边、三对角分别对应相等,则两个三角形全等.能否减少一些条件,找到更简便的判定两个三角形全等的方法呢?对两个三角形来说,六个元素(三条边、三对角)中至少要有几个元素对应相等,这两个三角形才会全等呢?如果两个三角形只有一组对应相等的元素,那么会出现几种可能的情况?这两个三角形会全等吗?两种,一组角或者边对应相等. 探究活动1试一试1. 画几个有一边长为 8 cm 的三角形,这样得到的三角形是否全等?有一条边对应相等的三角形不一定全等. 2. 画几个有一个角为 60° 的三角形,这样得到的三角形是否全等?有一个角对应相等的三角形不一定全等.归纳:如果两个三角形只有一组对应相等的元素,那么这两个三角形不一定全等.探究活动2 如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况?这两个三角形会全等吗?三种,一条边和一个角相等;两个角相等;两条边相等. 试一试 按照下面的条件,用刻度尺和量角器画三角形,并和周围的同学比较,所画的图形是否全等.(1) 三角形的一条边为 3 cm,一个内角为 30°.(1) 三角形的一条边为 3 cm,一个内角为 30°.30°3 cm3 cm3 cm30°30°(((一条边和一个内角相等不能判定两个三角形全等.30°70°(2) 三角形的两个内角分别为 30° 和 70°.两个内角对应相等不能判定两个三角形全等.(3) 三角形的两条边分别为 3 cm 和 5 cm.5 cm3 cm3 cm两条边对应相等不能判定两个三角形全等. 两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.思考: 如果两个三角形有三组对应相等的元素(边或角),又会如何呢?探索发现 1.如图,△ABC≌△CED, ∠B 和∠DEC 是对应角,BC 与 ED 是对应边,说出另两组对应角和对应边.解:对应角:∠A =∠DCE,∠D =∠ACB;对应边:AC = CD,AB = CE.ABCED当堂练习2. 如图,AD∥BC,AD = BC,AE⊥BC,将△ABE 沿 AD 方向平移,使点 A 与点 D 重合,点 E 平移至点 F,则 △ABE≌_____________,∠F =_____________. △DCF90°3.如图,点 D 是等腰直角三角形 ABC 内一点,AB=AC,将△ABD 绕点 A 逆时针旋转 90°,点 D 与点 E重合,则△ABD≌_________,AD=_________,BD=_______.△ACEAECE4. 如图,△ABC≌△AED,AB 是△ABC 的最大边,AE 是△AED 的最大边,∠BAC 与∠ EAD 是对应角,且∠BAC = 25°,∠B = 35°,AB = 3 cm,BC = 1 cm,求出∠E,∠ ADE 的度数和线段 DE,AE 的长度.解:∵ △ABC≌△AED(已知),∴∠E =∠B = 35°(全等三角形对应角相等),∠ADE =∠ACB =180°-25°-35°=120° (全等三角形对应角相等),DE = BC = 1 cm,AE = AB = 3cm(全等三角形对应边相等).3. 边角边1. 通过画图、操作、实验等教学活动,探索三角形全等的判定方法(S. A. S. ). (重点)2. 会用 S. A. S. 判定两个三角形全等. (难点)3. 灵活地运用所学的判定方法判定两个三角形全等,从而解决线段或角相等问题.学习目标 上节课给大家留了这样一个思考题,你们思考好了吗?如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?有四种情况:两边一角、两角一边、三角、三边.问题导入“S. A. S. ”判定三角形全等 如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗?— — 这是本节我们要探讨的课题. 如果已知一个三角形的两边及一角,那么有几种可能的情况呢?每一种情况得到的三角形都全等吗?应该有两种情况:一种是角夹在两条边的中间,形成两边夹一角另一情况是角不夹在两边的中间,形成两边一对角. 如果已知两个三角形有两边及一角对应相等时,应分为几种情形讨论?边-角-边AA'BB'CC'第一种边-边-角AA'B'CC'第二种B 如果已知两个三角形有两边及一角对应相等时,应分为几种情形讨论?做一做 如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.比一比:大家所画的三角形都全等吗?ABMC步骤:1. 画一线段 AB,使它等于4cm;2. 画∠MAB = 45°; 3. 在射线 AM 上截取 AC = 3cm; 4. 连结 BC. △ABC 就是所求做的三角形.试一试,换两条线段和一个角,是否有同样的结论.下面用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.DEF“边角边”判定三角形全等的方法文字语言:两边及其夹角分别相等的两个三角形全等.简记为 S. A. S. (或边角边).几何语言:在△ABC 和△ DEF 中,∴△ABC≌△DEF (S. A. S. ).必须是两边“夹角”例1 如图,已知线段 AC,BD 相交于点 E,AE = DE,BE = CE,求证:△ABE≌△DCE.证明:在△ABE 和△DCE 中,∴ △ABE≌△DCE (S. A. S.).例2如图,有一池塘,要测池塘两端 A、B 的距离,可先在平地上取一个可以直接到达 A 和 B 的点C,连接 AC 并延长到点 D,使 CD=CA,连接 BC 并延长到点 E,使CE=CB.C·ADBE连接 DE,那么量出 DE 的长就是 A、B 的距离,为什么?解:在△ABC 和△DEC 中,CA = CD (已知),∠ACB =∠DCE (对顶角相等),CB = CE (已知) ,∴△ABC≌△DEC (S. A. S.).∴ AB = DE (全等三角形的对应边相等).归纳证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.做一做 把你画的三角形与其他同学画的三角形进行对比,所画的三角形都全等吗?此时,符合条件的三角形有多少种?结论:两边及其一边所对的角相等 (即“边边角”对应相等或 S. S. A. ),两个三角形不一定全等.比一比1.如图,AC = BD,∠CAB =∠DBA,求证:BC = AD.证明:在 △ABC 与 △BAD 中,AC = BD (已知),∠CAB =∠DBA (已知),AB = BA (公共边),∴ △ABC≌△BAD (S. A. S. ).∴ BC = AD (全等三角形的对应边相等).当堂练习2.小兰做了一个如图所示的风筝,其中∠EDH =∠FDH,ED = FD ,将上述条件标注在图中,小明不用测量就能知道 EH = FH 吗?与同桌进行交流. 解:能. 在△EDH 和△FDH 中 , ED=FD,(已知) ∠EDH=∠FDH,(已知) DH=DH,(公共边)∴△EDH≌△FDH(S. A. S. ).∴EH=FH(全等三角形对应边相等).3. 已知:如图,AB = DB,CB = EB,∠1 = ∠2, 求证:∠A=∠D.证明:∵ ∠1=∠2,∴∠1 +∠DBC=∠2 +∠DBC,即∠ABC=∠DBE.在△ABC 和△DBE 中,AB=DB (已知), ∠ABC=∠DBE (已证), CB=EB (已知),∴△ABC≌△DBE ( S. A. S. ).∴∠A=∠D (全等三角形的对应角相等).4.如图,点 E、F 在 AC 上,AD∥BC,AD = CB, AE = CF. 求证:△AFD≌△CEB. 证明:∵ AD∥BC,∴ ∠A =∠C∵ AE = CF,∴ AE + EF = CF + EF,即 AF = CE.在△AFD 和△CEB 中,AD = CB (已知),∠A = ∠C (已证),AF = CE (已证), ∴△AFD≌△CEB ( S. A. S. ).4. 角边角1. 通过画图、操作、实验等教学活动,探索三角形全等的判定方法( A. S. A. ,A. A. S. ).(重点)2. 会用 A. S. A. ,A. A. S. 判定两个三角形全等.(难点)3. 灵活地运用所学的判定方法判定两个三角形全等,从而解决线段或角相等的问题.情境引入学习目标上节课,我们得到了全等三角形的一种判定方法,还记得吗?现在我们讨论两角一边的情况:如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形全等吗?S. A. S.可以分成两种情况:(1)两个角及这两角的夹边;(2)两个角及其中一角的对边.(角边角)(角角边) 如图,已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.“角边角”判定三角形全等步骤:1. 画一条线段 AB,使它等于 4 cm;2. 画∠MAB = 60°,∠NBA = 40°,MA 与 NB 交于点 C.△ABC 即为所求.4 cmABCMN 把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?换两个角和一条线段,试试看,是否有同样的结论.都全等60°40°4 cmABCMNDEF 下面用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.文字语言:两角及其夹边分别相等的两个三角形全等 (简写成“角边角”或“A. S. A. ”).“角边角”判定方法几何语言:在△ABC 和△A′B′C′ 中,∠A =∠A′ (已知), AB = A′B′ (已知),∠B =∠B′ (已知),∴△ABC≌△A′B′C′ ( A. S. A. ).已知:∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABC≌△DCB.证明:在△ABC 和△DCB 中,∠ABC=∠DCB (已知),例1 BC=CB (公共边), ∠ACB=∠DBC (已知),∴△ABC≌△DCB (A. S. A. ).“角角边”判定三角形全等 如图,如果两个三角形有两个角分别对应相等,且其中一组相等的角的对边相等,那么这两个三角形是否一定全等?(角角边)分析:因为三角形的内角和等于 180°,因此有两个角对应相等,那么第三个角必定对应相等,于是有“角边角”,可证得这两个三角形全等.已知:如图,∠A=∠A′,∠B=∠B′,AC=A′C′.求证: △ABC≌△A′B′C′.证明:∵∠A=∠A′,∠B=∠B′, ∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°(三角形内角和等于180°),∴∠C=∠C′ (等量代换).在△ABC 和△A′B′C′ 中,∵∠A=∠A′,AC=A′C′,∠C=∠C′, ∴△ABC≌△A′B′C′ ( A. S. A. )在△ABC 和△A′B′C′ 中,∠A =∠A′ (已知), ∠B =∠B′ (已知),AC = A′C′ (已知),∴ △ABC≌△A′B′C′ (A. A. S.).“角角边”判定方法例2 如图,点 D 在 AB 上,点 E 在 AC 上,AD = AE,∠B =∠C,求证:AB = AC.分析:证明△ACD≌△ABE,就可以得出 AB = AC.ABCDE证明:在△ACD 和△ABE 中,∠A =∠A(公共角 ), ∠C =∠B (已知 ),AD = AE(已知),∴ △ACD≌△ABE(A. A. S. ). ∴AB = AC. 例3求证:全等三角形对应边的高相等.已知:如图,△ABC≌△A′B′C′ ,AD,A′ D′ 分别是△ABC 和△A′B′C′ 的高.求证:AD= A′D′ .分析:从图中看出,AD,A′ D′ 分别属于△ABD 和△A′B′D′,要证 AD= A′D′,只需证明这两个三角形全等即可.证明:∵△ABC≌△A′B′C′ (已知),∴AB = A'B'(全等三角形的对应边相等), ∠B =∠B'(全等三角形的对应角相等).∵AD⊥BC,A'D'⊥B'C',∴∠ADB =∠A'D'B' = 90°(已知).在△ABD 和△A'B'D' 中,∠ADB =∠A'D'B' = 90°(已知),∠B =∠B' (已证),AB = A'B' (已证),∴△ABD≌△A'B'D'. ∴AD = A'D'. 1.如图,已知∠ACB =∠DBC,∠ABC =∠CDB,判别图中的两个三角形是否全等,并说明理由. 不全等,因为 BC 虽然是公共边,但不是对应边.当堂练习2.如图所示,OD=OB,AD∥BC,则全等三角形有( )(A) 2 对 (B) 3 对(C) 4 对 (D) 5 对C【解析】选C. 根据题意 AD∥BC 得∠ADO =∠CBO,∠DOA =∠BOC,又 OD = OB,所以△DOA≌△BOC.同理可证△DOC≌△BOA,△DAB≌△BCD,△ACD≌△CAB,所以有 4 对.3.如图,某同学将一块三角形玻璃打碎成了三块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )带(1)去 (B) 带(2)去(C) 带(3)去 (D) 带(1)(2)去C【解析】选C. 题干中图 (3) 包含原三角形的两角一边,根据“A. S. A. ”可配一块与原三角形玻璃完全一样的玻璃.4. 如图,∠ACB =∠DFE,BC = EF,那么应补充一个条件______________,才能使△ABC≌△DEF (写出一个即可).∠B = ∠EABCDEF∠B =∠E或∠A =∠D或 AC = DFAB = DE 可以吗?( A. S. A. )( A. A. S. )×AB∥DE( S. A. S. )5. 已知:如图,AB⊥BC,AD⊥DC,∠1 =∠2. 求证:AB = AD.证明:∵ AB⊥BC,AD⊥DC,∴∠B =∠D = 90°.在△ABC 和△ADC 中,∠1 =∠2 (已知), ∠B =∠D (已证),AC = AC (公共边),∴△ABC≌△ADC ( A. A. S. ).∴ AB = AD.5. 边边边1. 掌握三角形全等的“S. S. S. ”判定,并能应用它判别两个三角形是否全等,以及运用该条件解决一些简单的实际问题.(重点) 2. 由探索三角形全等条件的过程,体会由操作、归纳获得数学结论的过程.(难点)学习目标试一试1. 如右图,已知 AC = DB,∠ACB =∠DBC,则△ABC≌ ,理由是 ,且有∠ABC = ,AB = .△DCBS. A. S.∠DCBDC到目前为止,我们学习了哪几种判定三角形全等的方法?1. 根据定义;2. 基本事实:S. A. S. ,A. S. A. ;定理:A. A. S. .2. 如图,已知 AD 平分∠BAC,要使△ABD≌△ACD,(1)根据“S. A. S. ”需添加条件______________________(2)根据“A. S. A. ”需添加条件_____________________(3)根据“A. A. S. ”需添加条件_____________________AB = AC∠BDA =∠CDA∠B =∠C 若两个三角形有三个角对应相等,那么这两个三角形是否全等?画△ABC,其中∠A = 50°,∠B = 60°,∠C = 70°.ABCABCA B C 三个角对应相等的两个三角形不一定全等.“S. S. S. ”判定三角形全等 如果两个三角形有三条边分别对应相等,那么这两个三角形是否一定全等呢? 如图,已知三条线段 a,b,c,试画一个三角形,使这三条线段分别为其三边.如图,已知三条线段 a,b,c,试画一个三角形,使这三条线段分别为其三边.把你画的三角形与其他同学画的三角形相比较,它们全等吗?步骤:1.画一线段 AB 使它的长度等于c (4.5 cm).abcABC2. 以点 A 为圆心,以线段 b (3 cm) 的长为半径画圆弧;以点 B 为圆心,以线段 a (4 cm) 的长为半径画圆弧;两弧交于点 C.3. 连结 AC、BC.△ABC 即为所求.文字语言:三边分别相等的两个三角形全等,简写为“边边边”或“S. S. S. ”.“边边边”判定方法几何语言:在△ABC 和△DEF 中,AB = DE,BC = EF,CA = FD,∴△ABC≌△DEF (S. S. S. ).例1如图,有一个三角形钢架,AB = AC ,AD 是连接点 A 与 BC 中点 D 的支架.求证:△ABD ≌△ACD .解题思路:先找隐含条件再找现有条件最后找准备条件公共边 ADAB = ACBD = CDD 是 BC 的中点①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.证明的书写步骤:例2 如图,四边形 ABCD 中,AB = CD,AD = CB,求证:∠B =∠D例3 已知:如图,AC = AD,BC = BD. 求证: ∠C=∠D.ABCDABCD1. 判定三角形全等时最少有几组边对应相等?最多有几组边?2. 判定三角形全等时最少有几组角对应相等?最多有几组角?最少一组边,最多三组边.最少一组角,最多两组角.想一想1.如图,AB = CD,AC = BD,△ABC 和△DCB 是否全等?请完成下列解题步骤. ==ⅤⅤBC CB△DCBS. S. S. 2. 如图,D、F 是线段 BC 上的两点,AB = CE,AF = DE,要使△ABF≌△ECD,还需要条件____________ (填一个条件即可). BF = CD3. 已知:如图 ,AC = FE,AD = FB,BC = DE.求证:(1)△ABC≌△FDE证明:(1) ∵ AD = FB,∴ AB = FD (等式的性质).在△ABC 和△FDE 中,AC = FE (已知),BC = DE (已知),AB = FD (已证),∴△ABC≌△FDE ( S. S. S. ).==??√√ (2) ∠C = ∠E.∵△ABC≌△FDE (已证),∴∠C =∠E (全等三角形的对应角相等). 6.斜边直角边1.已知斜边、直角边会画直角三角形,经历画直角三角形探究得到“HL”定理,体会“HL”的合理性.(重点) 2.掌握“HL”定理,能正确应用“HL”定理证明两个三角形全等.(难点)学习目标3.能正确应用所学的全等三角形的判定定理解决问题.(难点)回顾与思考1. 全等三角形的对应边 ,对应角 . 2. 判定三角形全等的方法有:相等相等S. A. S. ,A. S. A. ,A. A. S. ,S. S. S. .再忆直角三角形Rt△ABC直角边斜边ABC直角边舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.(1) 你能帮他想个办法吗?根据“S. A. S. ”可测量其余两边与这两边的夹角.根据“A.S.A.”,“A.A.S.”可测量对应一边和一锐角.利用“H. L. ”判定直角三角形全等(2) 如果他只带一个卷尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等.于是,他就肯定“两个直角三角形是全等的”.斜边和一条直角边对应相等 → 两个直角三角形全等你相信这个结论吗?下面,让我们来验证这个结论. 如图,已知两条线段,试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.2 cm3 cmMABC1. 画一条线段 AB,使它等于 2 cm;2. 画∠MAB = 90°(用量角器或三角尺);3. 以点 B 为圆心、3 cm 长为半径画圆弧,交射线 AM 于 C;4. 连结 BC.△ABC 即为所求.把你画的直角三角形与其他同学画的直角三角形相比较,它们全等吗?步骤:文字语言:斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“H. L. ”).“S. S. A. ”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.几何语言:在 Rt△ABC 和 Rt△A′B′C′ 中,AB = A′B′,BC = B′C′,∴ Rt△ABC≌Rt△A′B′C′ (H. L. ). “斜边、直角边”判定方法如图,AC⊥BC,BD⊥AD,AC = BD,求证:BC = AD.证明:∵ AC⊥BC,BD⊥AD, ∴∠C 与∠D 都是直角.在 Rt△ABC 和 Rt△BAD 中, 例1 应用“H. L. ”的前提条件是在直角三角形中AB = BA,AC = BD .∴ Rt△ABC≌Rt△BAD (H. L.).∴ BC = AD.1. 如图,∠B =∠D = 90°,要证明△ABC 与△ADC 全等,还需要补充的条件是__________(写出一个即可).当堂练习答案: AB = AD 或 BC = DC 或 ∠BAC =∠DAC 或 ∠ACB =∠ACD2.如图,在△ABC 中,已知 BD⊥AC,CE⊥AB,BD = CE.求证:△EBC≌△DCB.证明: ∵ BD⊥AC,CE⊥AB,∴∠BEC =∠BDC = 90°.在 Rt△EBC 和 Rt△DCB 中,CE = BD, BC = CB .∴ Rt△EBC≌Rt△DCB (H. L. ).3. 如图,AB = CD, BF⊥AC,DE⊥AC,AE = CF.求证:BF = DE.证明:∵ BF⊥AC,DE⊥AC,∴∠BFA =∠DEC = 90°.∵ AE = CF,∴ AE + EF = CF + EF,即 AF = CE.在 Rt△ABF 和 Rt△CDE 中,AB = CD,AF = CE,∴ Rt△ABF≌Rt△CDE (H. L. ).∴ BF = DE.全等三角形全等三角形:能够完全重合的两个三角形叫做全等三角形.全等三角形的性质全等三角形的对应边相等全等三角形的对应角相等课堂小结两边及其夹角分别相等的两个三角形三角形全等的“S. A. S. ”判定:两边及其夹角分别相等的两个三角形全等“S. S. A. ”不能判定两个三角形全等注意:1. 已知两边,必须找“夹角”;2. 已知一角和这角的一夹边,必须找这角的另一夹边 课堂小结两角一边内容两角及其夹边分别相等的两个三角形全等(简写成“A. S. A. ”)应用为证明线段和角相等提供了新的证法注意注意“角角边”“角边角”中两角与边的区别两角和其中一角的对边分别相等的两个三角形全等.简写成“角角边”或“A. A. S. ”.课堂小结边边边内容三边分别相等的两个三角形全等(简写成“S. S. S. ”)应用思路分析书写步骤结合图形找隐含条件和现有条件,证准备条件四步骤1. 说明两三角形全等所需的条件应按对应边的顺序书写.2. 结论中所出现的边必须在所证明的两个三角形中. 课堂小结斜边直角边内容斜边和一条直角边分别相等的两个直角三角形全等.前提条件在直角三角形中使用方法只须找除直角外的两个条件即可(两个条件中至少有一个条件是一组对应边相等)课堂小结
13.2 三角形全等的判断1. 全等三角形1.理解全等三角形的概念,及全等三角形经过一系列变换后,能够完全重合的性质.(重点)2. 掌握全等三角形的性质(对应边相等,对应角相等)和判定条件.(难点)学习目标复习导入全等图形:能够完全重合的两个图形叫做全等图形.全等形包括规则图形和不规则图形全等.能够完全重合的两个三角形,叫做全等三角形记作:△ABC≌△DEF读作:△ABC全等于△DEF互相重合的顶点叫对应顶点.互相重合的边叫对应边.互相重合的角叫对应角.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.如图,已知△ABC≌△DEF 请指出图中的对应边和对应角.∠D∠BAD∠ABDADBDBAAB =AC =BC =∠BAC =∠ABC =∠C =归纳有公共边的,公共边一般是对应边.全等三角形如图,以直线 l 为对称轴,画出△ABC 的对称图形,并指出它们的对应顶点、对应边和对应角.若已知∠A = 60°,∠B = 80°,那么△DEF 的各个角的大小:∠D = ,∠E = ,∠F = . 60°80°40°l一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等.AACBABDCDBCABCE2. 全等三角形的判定条件全等三角形的判定条件怎么判断两个三角形全等呢? 根据全等三角形的定义可知:能够完全重合两个三角形全等,即两个三角形的三对边、三对角分别对应相等,则两个三角形全等.能否减少一些条件,找到更简便的判定两个三角形全等的方法呢?对两个三角形来说,六个元素(三条边、三对角)中至少要有几个元素对应相等,这两个三角形才会全等呢?如果两个三角形只有一组对应相等的元素,那么会出现几种可能的情况?这两个三角形会全等吗?两种,一组角或者边对应相等. 探究活动1试一试1. 画几个有一边长为 8 cm 的三角形,这样得到的三角形是否全等?有一条边对应相等的三角形不一定全等. 2. 画几个有一个角为 60° 的三角形,这样得到的三角形是否全等?有一个角对应相等的三角形不一定全等.归纳:如果两个三角形只有一组对应相等的元素,那么这两个三角形不一定全等.探究活动2 如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况?这两个三角形会全等吗?三种,一条边和一个角相等;两个角相等;两条边相等. 试一试 按照下面的条件,用刻度尺和量角器画三角形,并和周围的同学比较,所画的图形是否全等.(1) 三角形的一条边为 3 cm,一个内角为 30°.(1) 三角形的一条边为 3 cm,一个内角为 30°.30°3 cm3 cm3 cm30°30°(((一条边和一个内角相等不能判定两个三角形全等.30°70°(2) 三角形的两个内角分别为 30° 和 70°.两个内角对应相等不能判定两个三角形全等.(3) 三角形的两条边分别为 3 cm 和 5 cm.5 cm3 cm3 cm两条边对应相等不能判定两个三角形全等. 两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.思考: 如果两个三角形有三组对应相等的元素(边或角),又会如何呢?探索发现 1.如图,△ABC≌△CED, ∠B 和∠DEC 是对应角,BC 与 ED 是对应边,说出另两组对应角和对应边.解:对应角:∠A =∠DCE,∠D =∠ACB;对应边:AC = CD,AB = CE.ABCED当堂练习2. 如图,AD∥BC,AD = BC,AE⊥BC,将△ABE 沿 AD 方向平移,使点 A 与点 D 重合,点 E 平移至点 F,则 △ABE≌_____________,∠F =_____________. △DCF90°3.如图,点 D 是等腰直角三角形 ABC 内一点,AB=AC,将△ABD 绕点 A 逆时针旋转 90°,点 D 与点 E重合,则△ABD≌_________,AD=_________,BD=_______.△ACEAECE4. 如图,△ABC≌△AED,AB 是△ABC 的最大边,AE 是△AED 的最大边,∠BAC 与∠ EAD 是对应角,且∠BAC = 25°,∠B = 35°,AB = 3 cm,BC = 1 cm,求出∠E,∠ ADE 的度数和线段 DE,AE 的长度.解:∵ △ABC≌△AED(已知),∴∠E =∠B = 35°(全等三角形对应角相等),∠ADE =∠ACB =180°-25°-35°=120° (全等三角形对应角相等),DE = BC = 1 cm,AE = AB = 3cm(全等三角形对应边相等).3. 边角边1. 通过画图、操作、实验等教学活动,探索三角形全等的判定方法(S. A. S. ). (重点)2. 会用 S. A. S. 判定两个三角形全等. (难点)3. 灵活地运用所学的判定方法判定两个三角形全等,从而解决线段或角相等问题.学习目标 上节课给大家留了这样一个思考题,你们思考好了吗?如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?有四种情况:两边一角、两角一边、三角、三边.问题导入“S. A. S. ”判定三角形全等 如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗?— — 这是本节我们要探讨的课题. 如果已知一个三角形的两边及一角,那么有几种可能的情况呢?每一种情况得到的三角形都全等吗?应该有两种情况:一种是角夹在两条边的中间,形成两边夹一角另一情况是角不夹在两边的中间,形成两边一对角. 如果已知两个三角形有两边及一角对应相等时,应分为几种情形讨论?边-角-边AA'BB'CC'第一种边-边-角AA'B'CC'第二种B 如果已知两个三角形有两边及一角对应相等时,应分为几种情形讨论?做一做 如图,已知两条线段和一个角,试画一个三角形,使这两条线段为其两边,这个角为这两边的夹角.比一比:大家所画的三角形都全等吗?ABMC步骤:1. 画一线段 AB,使它等于4cm;2. 画∠MAB = 45°; 3. 在射线 AM 上截取 AC = 3cm; 4. 连结 BC. △ABC 就是所求做的三角形.试一试,换两条线段和一个角,是否有同样的结论.下面用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.DEF“边角边”判定三角形全等的方法文字语言:两边及其夹角分别相等的两个三角形全等.简记为 S. A. S. (或边角边).几何语言:在△ABC 和△ DEF 中,∴△ABC≌△DEF (S. A. S. ).必须是两边“夹角”例1 如图,已知线段 AC,BD 相交于点 E,AE = DE,BE = CE,求证:△ABE≌△DCE.证明:在△ABE 和△DCE 中,∴ △ABE≌△DCE (S. A. S.).例2如图,有一池塘,要测池塘两端 A、B 的距离,可先在平地上取一个可以直接到达 A 和 B 的点C,连接 AC 并延长到点 D,使 CD=CA,连接 BC 并延长到点 E,使CE=CB.C·ADBE连接 DE,那么量出 DE 的长就是 A、B 的距离,为什么?解:在△ABC 和△DEC 中,CA = CD (已知),∠ACB =∠DCE (对顶角相等),CB = CE (已知) ,∴△ABC≌△DEC (S. A. S.).∴ AB = DE (全等三角形的对应边相等).归纳证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.做一做 把你画的三角形与其他同学画的三角形进行对比,所画的三角形都全等吗?此时,符合条件的三角形有多少种?结论:两边及其一边所对的角相等 (即“边边角”对应相等或 S. S. A. ),两个三角形不一定全等.比一比1.如图,AC = BD,∠CAB =∠DBA,求证:BC = AD.证明:在 △ABC 与 △BAD 中,AC = BD (已知),∠CAB =∠DBA (已知),AB = BA (公共边),∴ △ABC≌△BAD (S. A. S. ).∴ BC = AD (全等三角形的对应边相等).当堂练习2.小兰做了一个如图所示的风筝,其中∠EDH =∠FDH,ED = FD ,将上述条件标注在图中,小明不用测量就能知道 EH = FH 吗?与同桌进行交流. 解:能. 在△EDH 和△FDH 中 , ED=FD,(已知) ∠EDH=∠FDH,(已知) DH=DH,(公共边)∴△EDH≌△FDH(S. A. S. ).∴EH=FH(全等三角形对应边相等).3. 已知:如图,AB = DB,CB = EB,∠1 = ∠2, 求证:∠A=∠D.证明:∵ ∠1=∠2,∴∠1 +∠DBC=∠2 +∠DBC,即∠ABC=∠DBE.在△ABC 和△DBE 中,AB=DB (已知), ∠ABC=∠DBE (已证), CB=EB (已知),∴△ABC≌△DBE ( S. A. S. ).∴∠A=∠D (全等三角形的对应角相等).4.如图,点 E、F 在 AC 上,AD∥BC,AD = CB, AE = CF. 求证:△AFD≌△CEB. 证明:∵ AD∥BC,∴ ∠A =∠C∵ AE = CF,∴ AE + EF = CF + EF,即 AF = CE.在△AFD 和△CEB 中,AD = CB (已知),∠A = ∠C (已证),AF = CE (已证), ∴△AFD≌△CEB ( S. A. S. ).4. 角边角1. 通过画图、操作、实验等教学活动,探索三角形全等的判定方法( A. S. A. ,A. A. S. ).(重点)2. 会用 A. S. A. ,A. A. S. 判定两个三角形全等.(难点)3. 灵活地运用所学的判定方法判定两个三角形全等,从而解决线段或角相等的问题.情境引入学习目标上节课,我们得到了全等三角形的一种判定方法,还记得吗?现在我们讨论两角一边的情况:如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形全等吗?S. A. S.可以分成两种情况:(1)两个角及这两角的夹边;(2)两个角及其中一角的对边.(角边角)(角角边) 如图,已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.“角边角”判定三角形全等步骤:1. 画一条线段 AB,使它等于 4 cm;2. 画∠MAB = 60°,∠NBA = 40°,MA 与 NB 交于点 C.△ABC 即为所求.4 cmABCMN 把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?换两个角和一条线段,试试看,是否有同样的结论.都全等60°40°4 cmABCMNDEF 下面用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.文字语言:两角及其夹边分别相等的两个三角形全等 (简写成“角边角”或“A. S. A. ”).“角边角”判定方法几何语言:在△ABC 和△A′B′C′ 中,∠A =∠A′ (已知), AB = A′B′ (已知),∠B =∠B′ (已知),∴△ABC≌△A′B′C′ ( A. S. A. ).已知:∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABC≌△DCB.证明:在△ABC 和△DCB 中,∠ABC=∠DCB (已知),例1 BC=CB (公共边), ∠ACB=∠DBC (已知),∴△ABC≌△DCB (A. S. A. ).“角角边”判定三角形全等 如图,如果两个三角形有两个角分别对应相等,且其中一组相等的角的对边相等,那么这两个三角形是否一定全等?(角角边)分析:因为三角形的内角和等于 180°,因此有两个角对应相等,那么第三个角必定对应相等,于是有“角边角”,可证得这两个三角形全等.已知:如图,∠A=∠A′,∠B=∠B′,AC=A′C′.求证: △ABC≌△A′B′C′.证明:∵∠A=∠A′,∠B=∠B′, ∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°(三角形内角和等于180°),∴∠C=∠C′ (等量代换).在△ABC 和△A′B′C′ 中,∵∠A=∠A′,AC=A′C′,∠C=∠C′, ∴△ABC≌△A′B′C′ ( A. S. A. )在△ABC 和△A′B′C′ 中,∠A =∠A′ (已知), ∠B =∠B′ (已知),AC = A′C′ (已知),∴ △ABC≌△A′B′C′ (A. A. S.).“角角边”判定方法例2 如图,点 D 在 AB 上,点 E 在 AC 上,AD = AE,∠B =∠C,求证:AB = AC.分析:证明△ACD≌△ABE,就可以得出 AB = AC.ABCDE证明:在△ACD 和△ABE 中,∠A =∠A(公共角 ), ∠C =∠B (已知 ),AD = AE(已知),∴ △ACD≌△ABE(A. A. S. ). ∴AB = AC. 例3求证:全等三角形对应边的高相等.已知:如图,△ABC≌△A′B′C′ ,AD,A′ D′ 分别是△ABC 和△A′B′C′ 的高.求证:AD= A′D′ .分析:从图中看出,AD,A′ D′ 分别属于△ABD 和△A′B′D′,要证 AD= A′D′,只需证明这两个三角形全等即可.证明:∵△ABC≌△A′B′C′ (已知),∴AB = A'B'(全等三角形的对应边相等), ∠B =∠B'(全等三角形的对应角相等).∵AD⊥BC,A'D'⊥B'C',∴∠ADB =∠A'D'B' = 90°(已知).在△ABD 和△A'B'D' 中,∠ADB =∠A'D'B' = 90°(已知),∠B =∠B' (已证),AB = A'B' (已证),∴△ABD≌△A'B'D'. ∴AD = A'D'. 1.如图,已知∠ACB =∠DBC,∠ABC =∠CDB,判别图中的两个三角形是否全等,并说明理由. 不全等,因为 BC 虽然是公共边,但不是对应边.当堂练习2.如图所示,OD=OB,AD∥BC,则全等三角形有( )(A) 2 对 (B) 3 对(C) 4 对 (D) 5 对C【解析】选C. 根据题意 AD∥BC 得∠ADO =∠CBO,∠DOA =∠BOC,又 OD = OB,所以△DOA≌△BOC.同理可证△DOC≌△BOA,△DAB≌△BCD,△ACD≌△CAB,所以有 4 对.3.如图,某同学将一块三角形玻璃打碎成了三块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )带(1)去 (B) 带(2)去(C) 带(3)去 (D) 带(1)(2)去C【解析】选C. 题干中图 (3) 包含原三角形的两角一边,根据“A. S. A. ”可配一块与原三角形玻璃完全一样的玻璃.4. 如图,∠ACB =∠DFE,BC = EF,那么应补充一个条件______________,才能使△ABC≌△DEF (写出一个即可).∠B = ∠EABCDEF∠B =∠E或∠A =∠D或 AC = DFAB = DE 可以吗?( A. S. A. )( A. A. S. )×AB∥DE( S. A. S. )5. 已知:如图,AB⊥BC,AD⊥DC,∠1 =∠2. 求证:AB = AD.证明:∵ AB⊥BC,AD⊥DC,∴∠B =∠D = 90°.在△ABC 和△ADC 中,∠1 =∠2 (已知), ∠B =∠D (已证),AC = AC (公共边),∴△ABC≌△ADC ( A. A. S. ).∴ AB = AD.5. 边边边1. 掌握三角形全等的“S. S. S. ”判定,并能应用它判别两个三角形是否全等,以及运用该条件解决一些简单的实际问题.(重点) 2. 由探索三角形全等条件的过程,体会由操作、归纳获得数学结论的过程.(难点)学习目标试一试1. 如右图,已知 AC = DB,∠ACB =∠DBC,则△ABC≌ ,理由是 ,且有∠ABC = ,AB = .△DCBS. A. S.∠DCBDC到目前为止,我们学习了哪几种判定三角形全等的方法?1. 根据定义;2. 基本事实:S. A. S. ,A. S. A. ;定理:A. A. S. .2. 如图,已知 AD 平分∠BAC,要使△ABD≌△ACD,(1)根据“S. A. S. ”需添加条件______________________(2)根据“A. S. A. ”需添加条件_____________________(3)根据“A. A. S. ”需添加条件_____________________AB = AC∠BDA =∠CDA∠B =∠C 若两个三角形有三个角对应相等,那么这两个三角形是否全等?画△ABC,其中∠A = 50°,∠B = 60°,∠C = 70°.ABCABCA B C 三个角对应相等的两个三角形不一定全等.“S. S. S. ”判定三角形全等 如果两个三角形有三条边分别对应相等,那么这两个三角形是否一定全等呢? 如图,已知三条线段 a,b,c,试画一个三角形,使这三条线段分别为其三边.如图,已知三条线段 a,b,c,试画一个三角形,使这三条线段分别为其三边.把你画的三角形与其他同学画的三角形相比较,它们全等吗?步骤:1.画一线段 AB 使它的长度等于c (4.5 cm).abcABC2. 以点 A 为圆心,以线段 b (3 cm) 的长为半径画圆弧;以点 B 为圆心,以线段 a (4 cm) 的长为半径画圆弧;两弧交于点 C.3. 连结 AC、BC.△ABC 即为所求.文字语言:三边分别相等的两个三角形全等,简写为“边边边”或“S. S. S. ”.“边边边”判定方法几何语言:在△ABC 和△DEF 中,AB = DE,BC = EF,CA = FD,∴△ABC≌△DEF (S. S. S. ).例1如图,有一个三角形钢架,AB = AC ,AD 是连接点 A 与 BC 中点 D 的支架.求证:△ABD ≌△ACD .解题思路:先找隐含条件再找现有条件最后找准备条件公共边 ADAB = ACBD = CDD 是 BC 的中点①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.证明的书写步骤:例2 如图,四边形 ABCD 中,AB = CD,AD = CB,求证:∠B =∠D例3 已知:如图,AC = AD,BC = BD. 求证: ∠C=∠D.ABCDABCD1. 判定三角形全等时最少有几组边对应相等?最多有几组边?2. 判定三角形全等时最少有几组角对应相等?最多有几组角?最少一组边,最多三组边.最少一组角,最多两组角.想一想1.如图,AB = CD,AC = BD,△ABC 和△DCB 是否全等?请完成下列解题步骤. ==ⅤⅤBC CB△DCBS. S. S. 2. 如图,D、F 是线段 BC 上的两点,AB = CE,AF = DE,要使△ABF≌△ECD,还需要条件____________ (填一个条件即可). BF = CD3. 已知:如图 ,AC = FE,AD = FB,BC = DE.求证:(1)△ABC≌△FDE证明:(1) ∵ AD = FB,∴ AB = FD (等式的性质).在△ABC 和△FDE 中,AC = FE (已知),BC = DE (已知),AB = FD (已证),∴△ABC≌△FDE ( S. S. S. ).==??√√ (2) ∠C = ∠E.∵△ABC≌△FDE (已证),∴∠C =∠E (全等三角形的对应角相等). 6.斜边直角边1.已知斜边、直角边会画直角三角形,经历画直角三角形探究得到“HL”定理,体会“HL”的合理性.(重点) 2.掌握“HL”定理,能正确应用“HL”定理证明两个三角形全等.(难点)学习目标3.能正确应用所学的全等三角形的判定定理解决问题.(难点)回顾与思考1. 全等三角形的对应边 ,对应角 . 2. 判定三角形全等的方法有:相等相等S. A. S. ,A. S. A. ,A. A. S. ,S. S. S. .再忆直角三角形Rt△ABC直角边斜边ABC直角边舞台背景的形状是两个直角三角形,工作人员想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量.(1) 你能帮他想个办法吗?根据“S. A. S. ”可测量其余两边与这两边的夹角.根据“A.S.A.”,“A.A.S.”可测量对应一边和一锐角.利用“H. L. ”判定直角三角形全等(2) 如果他只带一个卷尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等.于是,他就肯定“两个直角三角形是全等的”.斜边和一条直角边对应相等 → 两个直角三角形全等你相信这个结论吗?下面,让我们来验证这个结论. 如图,已知两条线段,试画一个直角三角形,使长的线段为其斜边、短的线段为其一条直角边.2 cm3 cmMABC1. 画一条线段 AB,使它等于 2 cm;2. 画∠MAB = 90°(用量角器或三角尺);3. 以点 B 为圆心、3 cm 长为半径画圆弧,交射线 AM 于 C;4. 连结 BC.△ABC 即为所求.把你画的直角三角形与其他同学画的直角三角形相比较,它们全等吗?步骤:文字语言:斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“H. L. ”).“S. S. A. ”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.几何语言:在 Rt△ABC 和 Rt△A′B′C′ 中,AB = A′B′,BC = B′C′,∴ Rt△ABC≌Rt△A′B′C′ (H. L. ). “斜边、直角边”判定方法如图,AC⊥BC,BD⊥AD,AC = BD,求证:BC = AD.证明:∵ AC⊥BC,BD⊥AD, ∴∠C 与∠D 都是直角.在 Rt△ABC 和 Rt△BAD 中, 例1 应用“H. L. ”的前提条件是在直角三角形中AB = BA,AC = BD .∴ Rt△ABC≌Rt△BAD (H. L.).∴ BC = AD.1. 如图,∠B =∠D = 90°,要证明△ABC 与△ADC 全等,还需要补充的条件是__________(写出一个即可).当堂练习答案: AB = AD 或 BC = DC 或 ∠BAC =∠DAC 或 ∠ACB =∠ACD2.如图,在△ABC 中,已知 BD⊥AC,CE⊥AB,BD = CE.求证:△EBC≌△DCB.证明: ∵ BD⊥AC,CE⊥AB,∴∠BEC =∠BDC = 90°.在 Rt△EBC 和 Rt△DCB 中,CE = BD, BC = CB .∴ Rt△EBC≌Rt△DCB (H. L. ).3. 如图,AB = CD, BF⊥AC,DE⊥AC,AE = CF.求证:BF = DE.证明:∵ BF⊥AC,DE⊥AC,∴∠BFA =∠DEC = 90°.∵ AE = CF,∴ AE + EF = CF + EF,即 AF = CE.在 Rt△ABF 和 Rt△CDE 中,AB = CD,AF = CE,∴ Rt△ABF≌Rt△CDE (H. L. ).∴ BF = DE.全等三角形全等三角形:能够完全重合的两个三角形叫做全等三角形.全等三角形的性质全等三角形的对应边相等全等三角形的对应角相等课堂小结两边及其夹角分别相等的两个三角形三角形全等的“S. A. S. ”判定:两边及其夹角分别相等的两个三角形全等“S. S. A. ”不能判定两个三角形全等注意:1. 已知两边,必须找“夹角”;2. 已知一角和这角的一夹边,必须找这角的另一夹边 课堂小结两角一边内容两角及其夹边分别相等的两个三角形全等(简写成“A. S. A. ”)应用为证明线段和角相等提供了新的证法注意注意“角角边”“角边角”中两角与边的区别两角和其中一角的对边分别相等的两个三角形全等.简写成“角角边”或“A. A. S. ”.课堂小结边边边内容三边分别相等的两个三角形全等(简写成“S. S. S. ”)应用思路分析书写步骤结合图形找隐含条件和现有条件,证准备条件四步骤1. 说明两三角形全等所需的条件应按对应边的顺序书写.2. 结论中所出现的边必须在所证明的两个三角形中. 课堂小结斜边直角边内容斜边和一条直角边分别相等的两个直角三角形全等.前提条件在直角三角形中使用方法只须找除直角外的两个条件即可(两个条件中至少有一个条件是一组对应边相等)课堂小结
相关资料
更多









