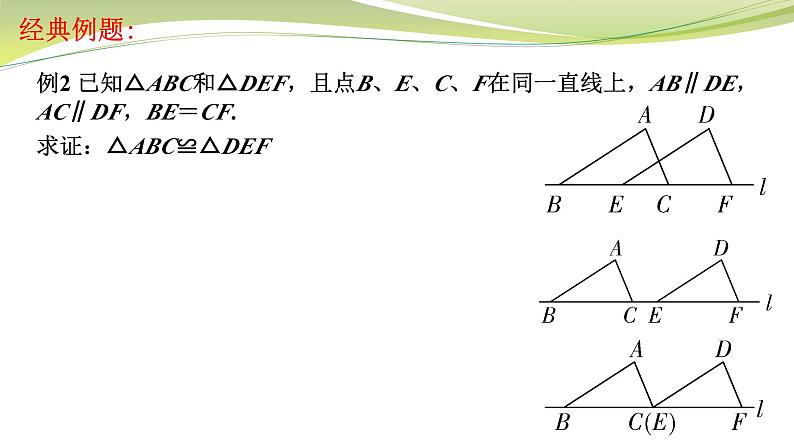
第1章 全等三角形 第1课时 苏科版数学八年级上册复习课件

这是一份第1章 全等三角形 第1课时 苏科版数学八年级上册复习课件，共22页。

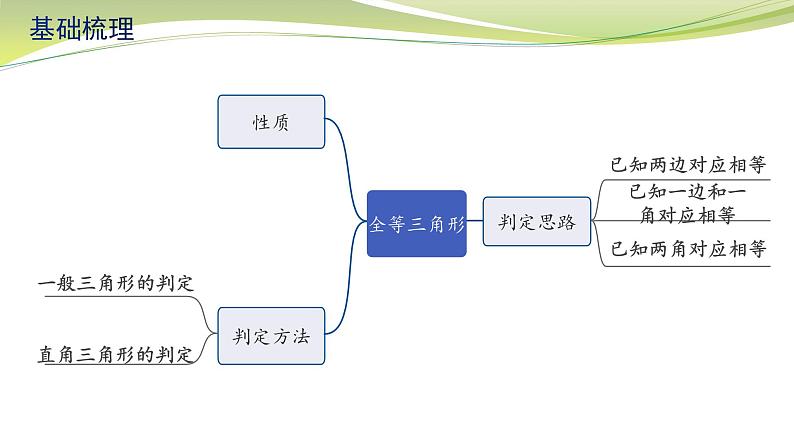
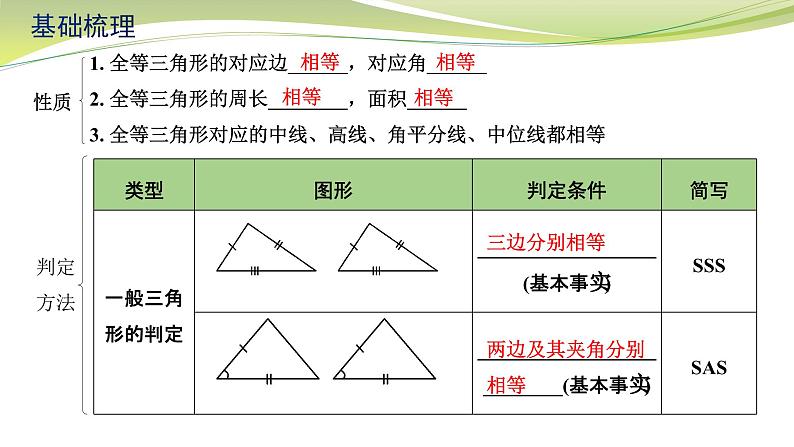
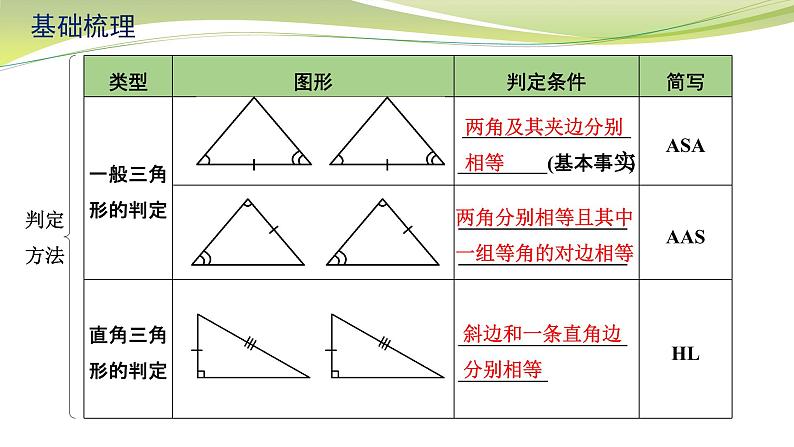
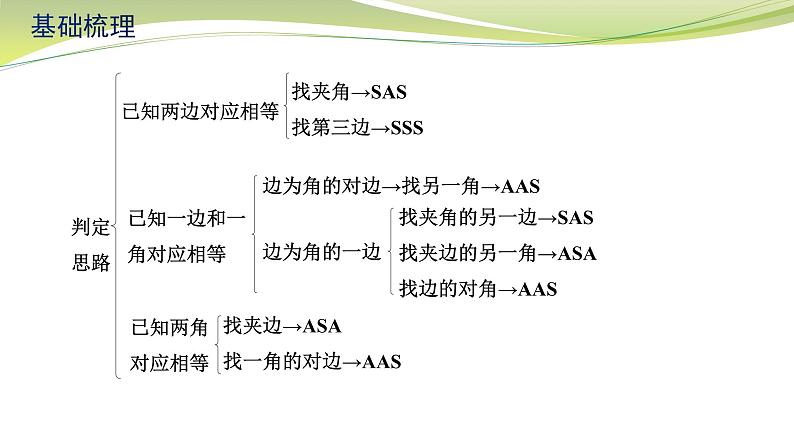
《全等三角形(1)》基础梳理全等三角形性质1. 全等三角形的对应边______，对应角______2. 全等三角形的周长________，面积______3. 全等三角形对应的中线、高线、角平分线、中位线都相等判定方法相等相等相等相等三边分别相等两边及其夹角分别相等基础梳理判定方法两角及其夹边分别相等　斜边和一条直角边分别相等两角分别相等且其中一组等角的对边相等基础梳理判定思路已知两边对应相等找夹角→SAS找第三边→SSS已知一边和一角对应相等边为角的对边→找另一角→AAS边为角的一边找夹角的另一边→SAS找夹边的另一角→ASA找边的对角→AAS已知两角对应相等找夹边→ASA找一角的对边→AAS基础梳理经典例题:例1.如图，已知△ABC≌△DEB，点E在AB上，DE与AC相交于点F．（1）当DE=9，BC=5时，线段 AE的长为 ，（2）已知∠D=35°，∠C=60°，求∠AFD的度数．4解：∵△ABC≌△DEB，∠C=60°（已知） ∴∠C=∠DBE=60°，∠A=∠D=35°（全等三角形对应角相等） ∵∠D+∠DBE+∠BED=180°（三角形内角和定理） ∠D=35°（已知） ∴∠ BED=180°-60°-35°=85°（等式性质） ∵ ∠BED+∠AEF=180° （平角定义） ∴ ∠AEF=95°（等式性质） ∴∠AFD=∠AEF+∠A=95°+35°=130° (三角形一个外角等于与它不相邻的两个内角和)策略总结:已知：全等对应元素：角 边 周长、面积 对应中线、高线、角平分线中位线……全等三角形性质例2 已知△ABC和△DEF，且点B、E、C、F在同一直线上，AB∥DE，AC∥DF，BE＝CF.经典例题:求证：△ABC≌△DEF策略总结:例3　已知：如图，AC、DB相交于点O，AB＝DC，∠ABO＝∠DCO.经典例题:求证：(1)△ABO≌△DCO；策略总结:策略总结:例4　如图，在四边形ABCD中，AD∥BC，AD＝BC，过点A作AE⊥AD交BD于点E，过点C作CF⊥BC交BD于点F，求证：△AED≌△CFB. 经典例题:△AEB≌△CFD；策略总结:策略总结:全等对应元素：角 边全等三角形判定图形变换：平移、旋转、 轴对称 （全等变换）课堂小练:第1题图课堂小练:第2题图3.如图，在△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G.(1)求证：EF＝BC；(2)若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．链接中考:(2019苏州24题8分)