第一章全等三角形小结-(苏科版) 课件PPT

这是一份第一章全等三角形小结-(苏科版) 课件PPT，共18页。

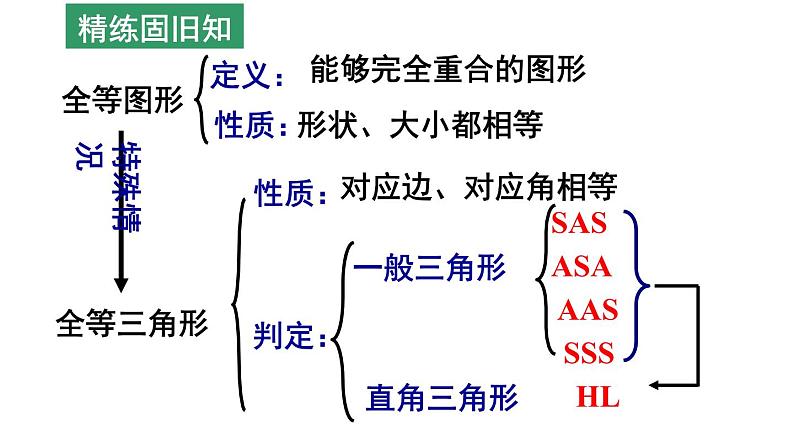
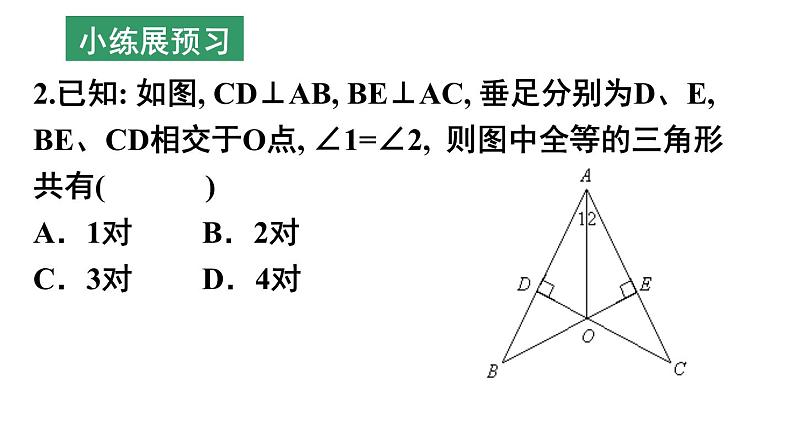
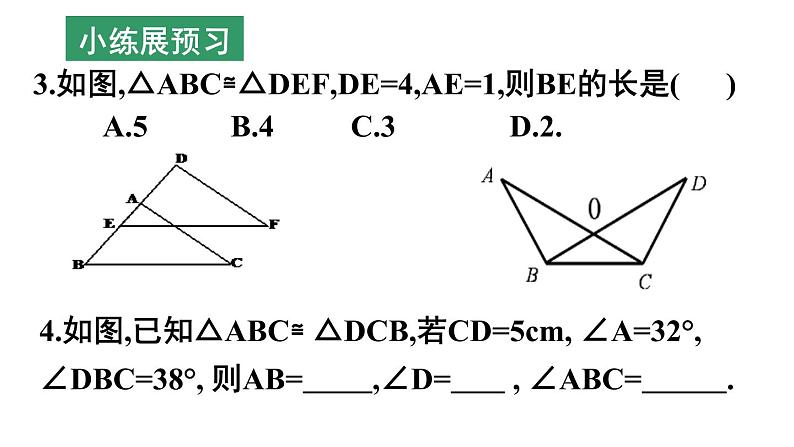
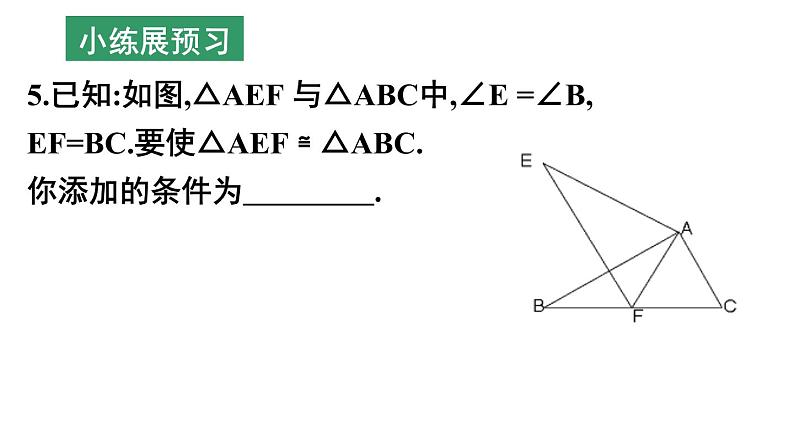
第1章 全等三角形  （小结与思考） 八年级(上册)初中数学全等图形全等三角形定义：能够完全重合的图形性质：形状、大小都相等对应边、对应角相等SASASAAASSSSHL精练固旧知证明两个三角形全等的基本思路：(1)已知两边(2)已知两角找第三边找夹角看是否是直角三角形找夹边找一角的对边证明两个三角形全等的基本思路：(3)已知一边一角已知一边与邻角已知一边与对角找这边的另一邻角找这个角的另一边找这边的对角找一角已知是直角，找另一边1.判断下列所叙述的图形是否是全等图形？(1)周长相等的所有正方形(2)有两条边相等的所有等腰三角形(3)有两条直角边相等的直角三角形(4)一条腰和一条底对应相等的等腰三角形(5)面积相等的所有圆(6)能够完全重合的多边形小练展预习2.已知: 如图, CD⊥AB, BE⊥AC, 垂足分别为D、E, BE、CD相交于O点, ∠1=∠2, 则图中全等的三角形共有( )A．1对 B．2对 C．3对 D．4对 小练展预习4.如图,已知△ABC≌ △DCB,若CD=5cm, ∠A=32°, ∠DBC=38°, 则AB= ,∠D= , ∠ABC= .3.如图,△ABC≌△DEF,DE=4,AE=1,则BE的长是( ) A.5 B.4 C.3 D.2.小练展预习5.已知:如图,△AEF 与△ABC中,∠E =∠B, EF=BC.要使△AEF ≌ △ABC.你添加的条件为 .小练展预习例1：如图，点B、E、C、F在一条直线上，AB＝DE，AB∥DE，∠A＝∠D．求证：BE=CF．AC与DF有怎样的关系？大练主课堂例2.如图:∠ACB=90°，AC=BC，BE ⊥ CE，AD⊥CE，垂足分别为E、D，图中有哪条线段与AD相等，说明理由.AD = CE大练主课堂1.如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断: ①AD=CB，②AE=CF，③∠B＝∠D，④ ∠A＝∠C.请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程.深练靠合作2.如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．求证：BC∥EF．深练靠合作3.如图，∠E=∠F=90°，∠B=∠C，AE=AF，下列结论：①EM=FN；②CD=DN；③∠FAN=∠EAM；④△ACN≌△ABM．其中正确的有( )A.1个 B.2个 C.3个 D.4个 深练靠合作4.如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC．求证：（1）EC=BF；（2）EC⊥BF．深练靠合作 5.如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点.如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．当点Q的运动速度为多少时，能够使△BPD与△CQP全等？深练靠合作ABC1.打开课本37页第12题：(1)速练在当堂ABC1.打开课本37页第12题：(2)速练在当堂2.打开课本37页第13题：速练在当堂