






- 2022秋高中数学第四章数列4.2等差数列4.2.1等差数列的概念第1课时等差数列的概念与通项公式课件新人教A版选择性必修第二册 课件 0 次下载
- 2022秋高中数学第四章数列4.2等差数列4.2.1等差数列的概念第2课时等差数列的性质课件新人教A版选择性必修第二册 课件 0 次下载
- 2022秋高中数学第四章数列4.2等差数列4.2.2等差数列的前n项和公式课件新人教A版选择性必修第二册 课件 0 次下载
- 2022秋高中数学第四章数列4.3等比数列4.3.1等比数列的概念第1课时等比数列的概念与通项公式课件新人教A版选择性必修第二册 课件 0 次下载
- 2022秋高中数学第四章数列4.3等比数列4.3.1等比数列的概念第2课时等比数列的性质课件新人教A版选择性必修第二册 课件 0 次下载
高中数学人教A版 (2019)选择性必修 第二册4.1 数列的概念课堂教学ppt课件
展开1.定义:按照确定的__________排列的一列数称为数列.2.项:数列中的____________叫做这个数列的项.a1称为数列{an}的第1项(或称为__________),a2称为第2项,…,an称为第n项.3.数列的表示:数列的一般形式可以写成a1,a2,a3,…,an,…,简记为__________.
【预习自测】(2022年南阳月考)(多选)下列有关数列的说法错误的是( )A.同一数列的任意两项均不可能相同B.数列-1,0,1与数列1,0,-1是同一个数列C.数列1,3,5,7可表示为{1,3,5,7}D.数列中的每一项都与它的序号有关
【答案】ABC【解析】同一个数在数列中可以重复出现,故A错误;数列是有序的,故数列-1,0,1与数列1,0,-1是不同的数列,故B错误;{1,3,5,7}为集合不是数列,故C错误;由数列的定义可知,数列中的每一项都与它的序号有关,故D正确.故选ABC.
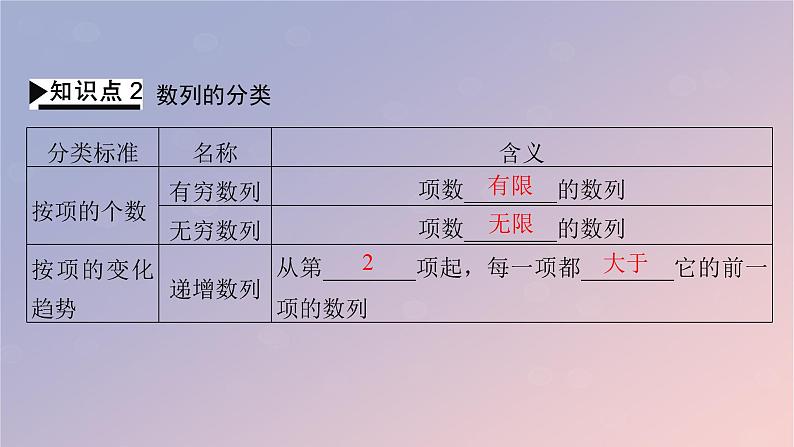
其中,有穷数列是________,无穷数列是________,递增数列是________,递减数列是________,常数列是________,摆动数列是________.(填序号)【答案】(1) (2)(3)(4) (3) (4) (1) (2)
如果数列{an}的第n项an与____________之间的对应关系可以用______________来表示,那么这个式子叫做这个数列的通项公式.
【预习自测】1.是不是所有数列都有通项公式?如果有,是否唯一?
2.数列与函数有何区别与联系?解:区别:数列的定义域为正整数集N*(或它的有限子集),而函数的定义域为实数集R(或它的子集).联系:数列是特殊的函数.
如果一个数列的____________或___________的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
【预习自测】在数列{an}中,已知a1=1,an+1=4an+1,则a3=________.【答案】21【解析】由题意知,a2=4a1+1=5,a3=4a2+1=21.
数列{an}的前n项和
Sn=a1+a2+…+an
【预习自测】已知数列{an}的前n项和Sn=n2+1,则an=________.
分别写出下列数列(数列的前4项已给出)的一个通项公式:
题型1 探求数列的通项公式
【解题探究】这样的问题需要由特殊到一般进行归纳,认真观察,深入分析内在规律,如:什么在变,什么不变,尤其是变化的量与相应的项数n有何关系,有时也可以以一些简单的数列为依据.
已知数列的前几项求通项公式的一般规律此类问题虽无固定模式,但有规律可循,主要靠观察(观察规律)、比较(比较已知数列)、归纳、转化(转化为特殊数列)、联想(联想常见的数列)等方法.具体方法为:①先统一项的结构,如都化成分数、根式等;②分析这一结构中变化的部分与不变的部分,探索变化部分的规律与对应序号间的函数解析式;③对于符号交替出现的情况,可先观察其绝对值,再以(-1)n或(-1)n+1处理符号;④对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.
已知数列{an}的通项公式为an=3n2-28n.(1)写出数列的前3项;(2)-49和68是该数列的项吗?若是,是第几项?若不是,请说明理由.解:(1)∵an=3n2-28n,∴a1=3×12-28×1=-25,a2=3×22-28×2=-44,a3=3×32-28×3=-57.
题型2 数列通项公式的应用
通项公式的应用主要包括的两个方面(1)由通项公式写出数列的前几项.主要是对n进行取值,然后代入通项公式,相当于函数中,已知函数解析式和自变量的值求函数值;(2)判断一个数是否为该数列中的项.可由通项公式等于这个数解出n,根据n是否有正整数解便可确定这个数是否为数列中的项.
【解题探究】将已知等式进行变形,利用“累乘求积”得到通项公式.
题型3 由递推公式求数列中的项或通项
3.已知数列{an}中,a1=0,an+1=an+2n-1(n∈N*).根据数列的首项和递推公式,写出它的前五项并猜想出该数列的一个通项公式.解:由条件得a1=0,a2=0+1=1=12,a3=1+(2×2-1)=4=22,a4=4+(2×3-1)=9=32,a5=9+(2×4-1)=16=42,由以上各项猜想出数列的一个通项公式为an=(n-1)2.
(2021年上海期末)数列{an}的前n项和Sn满足Sn=n2+2n+3,n∈N*,则数列{an}的通项公式为an=________.
题型4 由前n项和Sn求通项公式
已知Sn,求an的步骤(1)当n=1时,a1=S1;(2)当n≥2时,an=Sn-Sn-1;(3)对n=1时的情况进行检验,若适合n≥2的通项则可以合并;若不适合则写成分段函数形式.
4.已知数列的前n项和为Sn,且满足Sn=an+n2-1,则{an}的通项公式为an=________.【答案】2n+1【解析】当n≥2时,Sn=an+n2-1,Sn-1=an-1+(n-1)2-1,两式相减得an=an-an-1+2n-1,即an-1=2n-1,也即an=2n+1(n≥1),又∵S2=a2+22-1=a2+3,∴a1+a2=a2+3,∴a1=3=2×1+1,∴{an}的通项公式为an=2n+1.
已知数列{an}满足a1a2a3…an=n2(n∈N*),求an.
易错警示 对递推公式变形时忽略n取值的变化而致误
1.(题型1)(2022年东莞期末)数列-3,-1,1,3,5,…的一个通项公式为( )A.an=-2n-5B.an=-2n-1C.an=2n-5D.an=2n-1【答案】C【解析】-3,-1,1,3,5,…,由分析可得a1=2×1-5=-3,a2=2×2-5=-1,a3=2×3-5=1,a4=2×4-5=3,故an=2n-5.故选C.
【答案】ABCD【解析】可以验证,当n为奇数时,A,B,C,D对应的项均为1;当n为偶数时,A,B,C,D对应的项均为0.
人教A版 (2019)选择性必修 第二册4.1 数列的概念课文内容ppt课件: 这是一份人教A版 (2019)选择性必修 第二册4.1 数列的概念课文内容ppt课件,共20页。PPT课件主要包含了新知初探·课前预习,题型探究·课堂解透,一个式子,Sn-Sn-1,答案D,答案C等内容,欢迎下载使用。
高中数学第四章 数列4.1 数列的概念图片课件ppt: 这是一份高中数学第四章 数列4.1 数列的概念图片课件ppt,共26页。PPT课件主要包含了新知初探·课前预习,题型探究·课堂解透,确定的顺序,每一个数,第1项,第n项,要点二数列的分类,答案B,答案C,答案D等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第二册4.1 数列的概念课文配套课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第二册4.1 数列的概念课文配套课件ppt,共35页。














