高中数学人教A版 (2019)选择性必修 第二册4.2 等差数列背景图课件ppt

这是一份高中数学人教A版 (2019)选择性必修 第二册4.2 等差数列背景图课件ppt，共41页。PPT课件主要包含了自学导引，倒序相加法，答案7839，答案B，答案C，答案A，答案8，课堂互动，素养训练等内容，欢迎下载使用。

等差数列前n项和公式是用____________推导的．
等差数列前n项和公式的推导
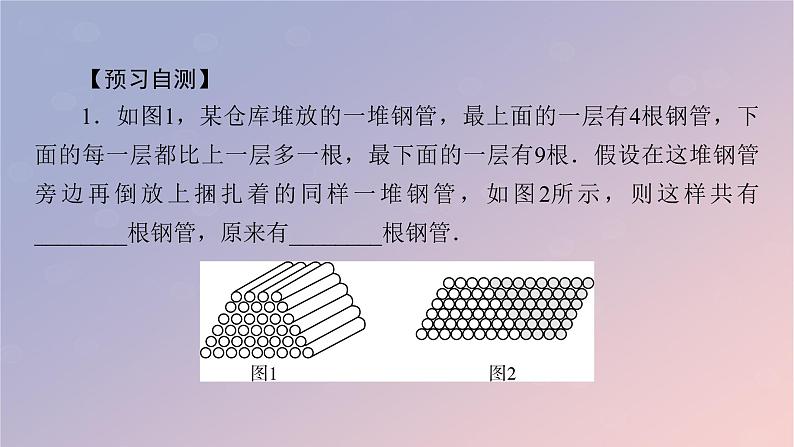
【预习自测】1．如图1，某仓库堆放的一堆钢管，最上面的一层有4根钢管，下面的每一层都比上一层多一根，最下面的一层有9根．假设在这堆钢管旁边再倒放上捆扎着的同样一堆钢管，如图2所示，则这样共有________根钢管，原来有________根钢管．
2．能否利用前面的问题推导等差数列前n项和公式Sn＝a1＋a2＋…＋an?
等差数列{an}的前n项和公式
1．若a1<0，d>0，则等差数列的前面若干项为负数项(或0)，所以将这些项相加即得Sn的最______值．2．若a1>0，d<0，则等差数列的前面若干项为正数项(或0)，所以将这些项相加即得Sn的最______值．特别地，若a1>0，d>0，则______是Sn的最小值；若a1<0，d<0，则______是Sn的最大值．
等差数列前n项和Sn的最值
【预习自测】1．设Sn是公差小于零的等差数列{an}的前n项和，且a1>0，若S5＝S9，则当Sn最大时，n＝(　　)A．6B．10C．7D．9【答案】C【解析】因为公差不为零的等差数列的前n项和Sn是关于n的二次函数，S5＝S9，所以对称轴为n＝7，又因为开口向下，所以当n＝7时，Sn有最大值．
2．已知等差数列{an}中，Sn是它的前n项和，若S16＞0，且S17＜0，则当Sn取最大值时n的值为(　　)A．7　　B．8C．9　　D．16【答案】B
已知数列{an}为等差数列，Sn为{an}的前n项和，d为{an}的公差．
题型1　有关等差数列的前n项和的基本运算
【解题探究】合理地使用等差数列的前n项和公式，注意其变形及应用方程的思想．
等差数列基本运算的解题方法a1，d，n称为等差数列的三个基本量，an和Sn都可以用这三个基本量来表示，五个量a1，d，n，an，Sn中可知三求二，即等差数列的通项公式及前n项和公式中“知三求二”的问题，一般是通过通项公式和前n项和公式联立方程(组)求解．这种方法是解决数列运算的基本方法，在具体求解过程中应注意已知与未知的联系及整体思想的运用．
1．设Sn是等差数列{an}的前n项和，若a1＝2，a5＝3a3，则S10＝(　　)A．－92B．－70C．54D．80【答案】B
题型2　等差数列前n项和性质的应用
等差数列的前n项和的常用性质(1)等差数列的依次k项之和，Sk，S2k－Sk，S3k－S2k，…组成公差为k2d的等差数列．
2．(1)在等差数列{an}中，Sn为{an}的前n项和，若S4＝1，S8＝4，则a17＋a18＋a19＋a20的值为(　　)A．9　　B．12C．16　　D．18(2)等差数列{an}中，a2＋a7＋a12＝24，则{an}的前13项和S13＝________．【答案】(1)A　(2)104
在等差数列{an}中，a1＝25，S17＝S9，求前n项和Sn的最大值．
题型3　等差数列前n项和的最值
3．已知{an}是一个等差数列且a2＝1，a5＝－5.(1)求{an}的通项公式an；(2)求{an}前n项和Sn的最大值．
已知等差数列{an}的通项公式为an＝5n－95，求当n为何值时Sn取最小值．【错解】由题意得，an＝5n－95＜0，解得n＜19，∴n＝18时，Sn有最小值．【错因】错解的原因是忽略了a19＝0，所以S18＝S19，即n＝18或n＝19时前n项和相等且最小．【正解】由题意得，an＝5n－95≤0，解得n≤19，∴等差数列{an}的前18项为负数，第19项为0，从第20项开始为正数，∴Sn取最小值时，n的值为18或19.
易错警示　忽略等差数列中为零的项
2．等差数列前n项和的性质在等差数列{an}中，Sn为其前n项和，则①S2n＝n(a1＋a2n)＝…＝n(an＋an＋1)；②S2n－1＝(2n－1)an；③当项数为偶数2n时，S偶－S奇＝nd，S奇∶S偶＝an∶an＋1；项数为奇数2n－1时，S奇－S偶＝an，S奇∶S偶＝n∶(n－1)．
1．(题型1)若等差数列{an}的前5项和S5＝25且a2＝3，则a7＝(　　)A．12B．13C．14D．15【答案】B【解析】由S5＝5a3＝25，得a3＝5，∴d＝a3－a2＝5－3＝2，∴a7＝a2＋5d＝3＋10＝13.
2．(题型2)在等差数列{an}中，Sn为其前n项和，若a3＋a4＋a8＝25，则S9＝(　　)A．60　B．75C．90　　D．105【答案】B
3．(题型3)(2022年长春月考)已知等差数列{an}的前n项和为Sn，若S13＜0，S12＞0，则在数列中绝对值最小的项为(　　)A．第5项　　B．第6项C．第7项　　D．第8项【答案】C
4．(题型3)(2021年成都期末)记Sn为等差数列{an}的前n项和，且a1＝22，S7＝S16，则Sn取最大值时n的值为________．【答案】11或12【解析】设等差数列{an}的公差为d，由S7＝S16，得7a1＋21d＝16a1＋120d，即a1＋11d＝0，又因为a1＝22，所以d＝－2，所以an＝22－2(n－1)＝24－2n，令an＝0，可得n＝12，所以数列{an}满足当n≤11时，an＞0；当n＝12时，an＝0；当n≥13时，an＜0，所以Sn取得最大值时，n的取值为11或12.