






高中数学人教A版 (2019)选择性必修 第二册4.3 等比数列课文ppt课件
展开【预习自测】1.(2021年哈尔滨四模)等比数列{an}满足a1+a2=2,a2+a3=4,则a9+a10=( )A.28 B.29C.210 D.211【答案】B
2.(2021年绵阳期中)已知等比数列{an}中,a2·a4·a6·a8=16,则a3·a7=( )A.±4B.4C.8D.±8【答案】B
在等比数列{an}中,已知a4a7=-512,a3+a8=124且公比为整数,求a10.
题型1 等比数列性质的应用
【解题探究】利用若m+n=k+l,则aman=akal解题.
1.各项为正数的等比数列{an}中,a4·a7=8,则lg2a1+lg2a2+…+lg2a10=( )A.5 B.10C.15 D.20【答案】C【解析】由等比数列的性质,得a1a10=a2a9=…=a4a7=…=8,∴lg2a1+lg2a2+…+lg2a10=lg2(a1·a2·…·a10)=lg285=15.
已知四个数前三个成等差数列,后三个成等比数列,中间两数之积为16,首尾两数之积为-128,求这四个数.
题型2 灵活设项求解等比数列
【解题探究】求四个数,给出四个条件,若列四个方程组成方程组虽可解,但较麻烦,因此可依据条件减少未知数的个数.设未知数时,可根据前三个数成等差数列来设,也可以依据后三个数成等比数列来设,还可以依据中间(或首尾)两数之积来设,关键是要把握住未知量要尽量少,下一步运算要简捷.
2.三个正数成等差数列,它们的和等于15,如果它们分别加上1,3,9,就成为等比数列,求这三个数.
某工厂2020年1月的生产总值为a万元,计划从2020年2月起,每月生产总值比上一个月增长m%,那么到2021年8月底该厂的生产总值为多少万元?解:设从2020年1月开始,第n个月该厂的生产总值是an万元,则an+1=an(1+m%),
题型3 等比数列的实际应用
【解题探究】将实际问题转化为等比数列模型,利用等比数列的知识解决.
解决数列实际应用题的方法数列实际应用题常与现实生活和生产实际中的具体事件相联系,建立数学模型是解决这类问题的核心,常用的方法有:(1)构造数列的模型,然后用数列的通项公式或求和公式解;(2)通过归纳得到结论,再用数列知识求解.
3.一种专门占据内存的计算机病毒开始时占据内存2 KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后________分钟,该病毒占据内存64 MB(1 MB=210KB).【答案】45【解析】由题意可得每3分钟病毒占的内存容量构成一个等比数列,令病毒占据64 MB时自身复制了n次,即2×2n=64×210=216,解得n=15,从而复制的时间为15×3=45(分).
在1和4之间插入三个数,使这五个数成等比数列,求插入的这三个数的乘积.
易错警示 利用等比中项性质时忽视符号判断
【错因】该解法没有正确判断a3的符号,在求等比数列的各项时,要注意正负号的选择.
【警示】在等比数列中,隔项的符号是一致的,故本题中a3=2.
3.(题型2)一个等比数列的前3项的积为2,后三项的积为4,且所有项的积为64,则该数列共有( )A.6项 B.8项C.10项 D.12项【答案】D
4.(题型2)(2022年抚州月考)在1和100之间插入n个正数,使这(n+2)个数成等比数列,则插入的这n个正数的积为________.【答案】10n
高中数学人教A版 (2019)选择性必修 第二册4.3 等比数列图片ppt课件: 这是一份高中数学人教A版 (2019)选择性必修 第二册4.3 等比数列图片ppt课件,共29页。
人教A版 (2019)选择性必修 第二册4.3 等比数列授课ppt课件: 这是一份人教A版 (2019)选择性必修 第二册4.3 等比数列授课ppt课件,共29页。
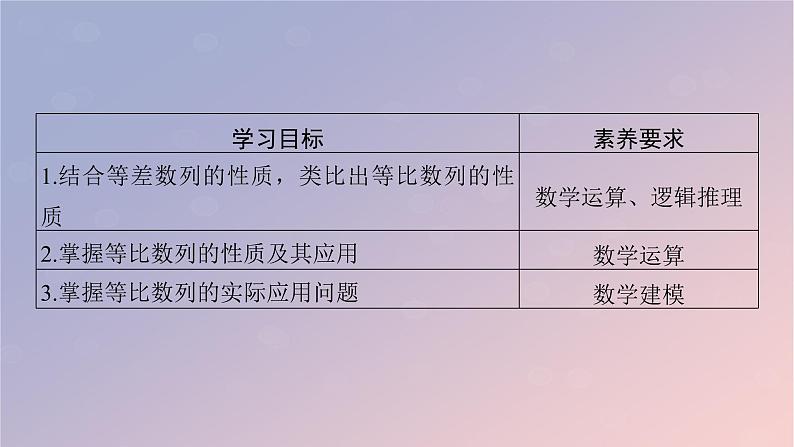
数学选择性必修 第二册第四章 数列4.3 等比数列图文课件ppt: 这是一份数学选择性必修 第二册第四章 数列4.3 等比数列图文课件ppt,共53页。PPT课件主要包含了3等比数列,素养目标·定方向,必备知识·探新知,a1qn-1,常数列,qn-m,ap·aq,an-1,an-k+1,q1·q2等内容,欢迎下载使用。













