高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数学案设计

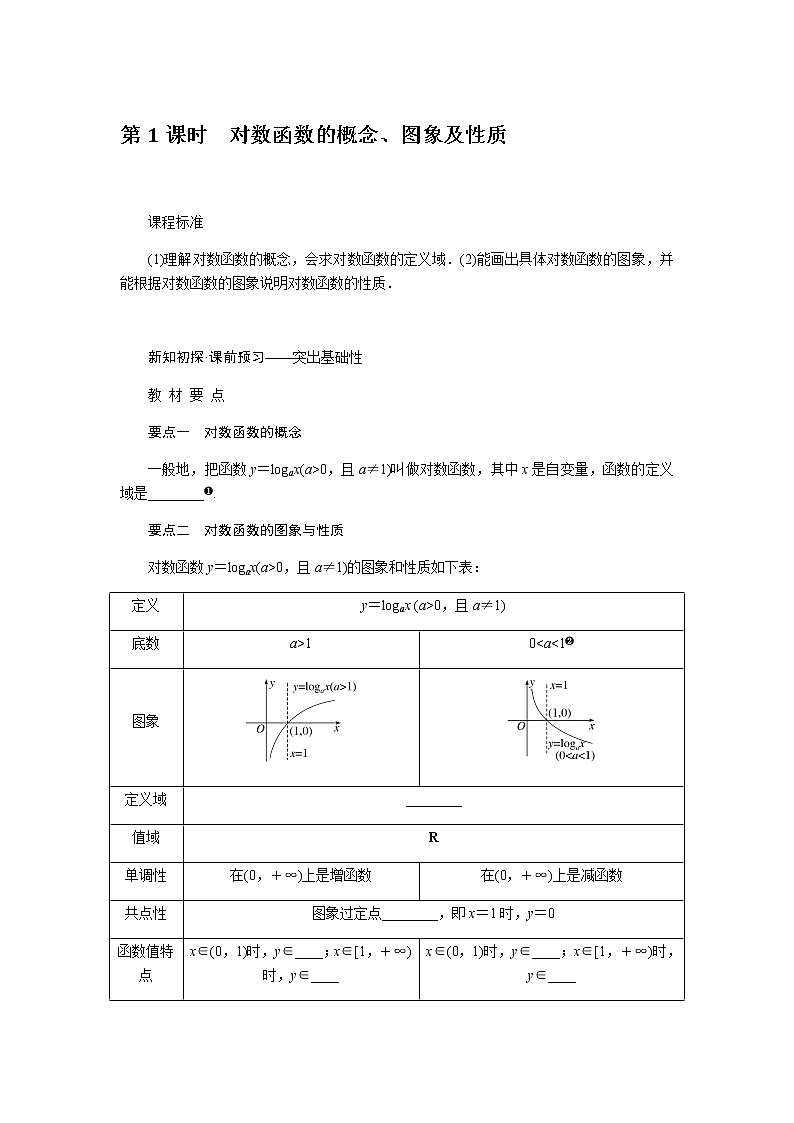
第1课时　对数函数的概念、图象及性质

课程标准

(1)理解对数函数的概念，会求对数函数的定义域．(2)能画出具体对数函数的图象，并能根据对数函数的图象说明对数函数的性质．

新知初探·课前预习——突出基础性

教 材 要 点

要点一　对数函数的概念

一般地，把函数y＝logax(a>0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是________❶.

要点二　对数函数的图象与性质

对数函数y＝logax(a>0，且a≠1)的图象和性质如下表：

要点三　反函数

指数函数______(a>0，且a≠1)与对数函数y＝______互为反函数❸.

助 学 批 注

批注❶　由指数式与对数式的关系知，对数函数的自变量x恰好是指数函数的函数值y，所以对数函数的定义域是(0，＋∞)．

批注❷　底数a与1的大小关系决定了对数函数图象的“升降”：当a＞1时，对数函数的图象“上升”；当0＜a＜1时，对数函数的图象“下降”．

批注❸　图象关于直线y＝x对称．

基 础 自 测

1．思考辨析(正确的画“√”，错误的画“×”)

(1)y＝log2x2是对数函数．(　　)

(2)对数函数的图象一定在y轴的右侧．(　　)

(3)函数y＝loga(x＋1)的定义域为(0，＋∞)．(　　)

(4)函数y＝log2x与y＝x2互为反函数．(　　)

2．对数函数的图象过点M(125，3)，则此对数函数的解析式为(　　)

A．y＝log5x    B．y＝

C．y＝    D．y＝log3x

3.函数y＝logax的图象如图所示，则实数a的可能取值为(　　)

A．5        B．

C．        D．

4．函数f(x)＝log0.5(x－1)的定义域是________．

题型探究·课堂解透——强化创新性

题型 1　对数函数的概念

例1　(1)指出下列函数是对数函数的是(　　)

A．y＝3log2x    B．y＝log6x

C．y＝logx3     D．y＝log2x＋1

(2)对数函数f(x)的图象过点(3，－2)，则f()＝________．

方法归纳

判断一个函数是对数函数的方法

巩固训练1　已知函数f(x)＝(2m2－m)logax＋m－1是对数函数，则m＝________．

　对数型函数的定义域

例2　求下列函数的定义域．

(1)y＝loga(3－x)＋loga(3＋x)；

(2)y＝log2(16－4x)．

(3)f(x)＝log(2x－1)(－4x＋8)．

方法归纳

求对数型函数的方法

除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数大于零且不等于1.

巩固训练2　(1)函数y＝ln (4－x)＋的定义域为(　　)

A．(0，4)    B．(0，4]

C．[0，4)    D．[0，4]

(2)函数f(x)＝的定义域为________．

题型 3 对数函数的图象

例3　(1)如图所示的曲线是对数函数y＝

logax，y＝logbx，y＝logcx，y＝logdx的图象，则a，b，c，d与1的大小关系为________．

(2)已知函数y＝loga(x＋3)－1(a＞0，且a≠1)的图象恒过定点A，若点A也在函数f(x)＝3x＋b的图象上，则f(log32)＝________．

方法归纳

解与对数函数图象有关问题的策略

巩固训练3　(1)函数y＝lg (x＋1)的图象大致是(　　)

(2)已知函数y＝loga(x－3)－1的图象恒过定点P，则点P的坐标是________．

第1课时　对数函数的概念、图象及性质

新知初探·课前预习

[教材要点]

要点一

(0，＋∞)

要点二

(0，＋∞)　(1，0)　(－∞，0)　[0，＋∞)　(0，＋∞)　(－∞，0]　x轴

要点三

y＝ax　logax(a>0且a≠1)

[基础自测]

1．答案：(1)×　(2)√　(3)×　(4)×

2．解析：设函数解析式为y＝logax(a>0，且a≠1)．

由于对数函数的图象过点M(125，3)，

所以3＝loga125，得a＝5.

所以对数函数的解析式为y＝log5x.

答案：A

3．解析：由图可知，a>1.

答案：A

4．解析：要使函数f(x)＝log0.5(x－1)有意义就要x－1>0，即x>1，所以函数f(x)＝log0.5(x－1)的定义域是(1，＋∞)．

答案：(1，＋∞)

题型探究·课堂解透

例1　解析：(1)A中log2x的系数是3，不是1，不是对数函数．

B符合对数函数的结构形式，是对数函数．

C中自变量在底数位置上，不是对数函数．

D中对数式log2x后又加1，不是对数函数．

(2)设f(x)＝logax，则loga3＝－2，∴a－2＝3，

∴a＝，∴f(x)＝，

∴f()＝＝－1.

答案：(1)B　(2)－1

巩固训练1　解析：因为函数f(x)是对数函数，则解得m＝1.

答案：1

例2　解析：(1)由得－3<x<3，

∴函数的定义域是(－3，3)．

(2)由16－4x>0，得4x<16＝42，

由指数函数的单调性得x<2，

∴函数y＝log2(16－4x)的定义域为(－∞，2)．

(3)由题意得解得

故函数y＝log(2x－1)(－4x＋8)的定义域为.

巩固训练2　解析：(1)函数y＝ln (4－x)＋，要使函数有意义可得，

解得0≤x<4，所以函数的定义域为[0，4)．

(2)由函数的解析式可知：⇒2<x≤4且x≠3，

所以函数的定义域为：(2，3)

答案：(1)C　(2)(2，3)

例3　解析：(1)由题图可知函数y＝logax，y＝logbx的底数a＞1，b＞1，函数y＝logcx，y＝logdx的底数0＜c＜1，0＜d＜1.

过点(0，1)作平行于x轴的直线，则直线与四条曲线交点的横坐标从左向右依次为c，d，a，b，显然b＞a＞1＞d＞c.

(2)依题意可知定点A(－2，－1)，f(－2)＝3－2＋b＝－1，b＝－，故f(x)＝3x－，f(log32)＝3log32－＝2－＝.

答案：(1)b>a>1>d>c　(2)

巩固训练3　解析：(1)由底数大于1可排除A、B，y＝lg (x＋1)可看作是y＝lg x的图象向左平移1个单位．(或令x＝0得y＝0，而且函数为增函数)．

(2) y＝logax的图象恒过点(1，0)，令x－3＝1，得x＝4，则y＝－1.

答案：(1)C　(2)(4，－1)