高中数学人教A版 (2019)必修 第一册4.4 对数函数习题

专题09 高分必刷题-对数函数名校重难点题型分类（解析版）

题型一：对数与对数运算

1.（师大）已知函数，则_________.

【解析】。

2.（一中）已知，，用、表示，则________.

【解析】∵，∴，所以

．

3.（长郡）__________.

【解析】原式=2-2+2=2.

4.（雅礼）计算：________．

【解析】原式=.

5.(师大)

【解析】原式.

6. （师大）计算__________.

【解析】原式=.

7.（明德）计算：.

【解析】

.

8.   （长郡）已知，且，则实数的值为_________.

已知，且，则实数的值为　　．

【解答】解：，，，又，即，

解得，故答案为：

9. （师大）已知函数，则(    )

A.  B.  C.  D.

【答案】．

题型二：对数函数的定义域

10.（明德）函数的定义域为(   )

A.    B.    C.    D.

11.（地质中学）函数的定义域___________.

【解析】，.

12. (师大)设集合，，则（    ）

A.  B.  C.  D.

【答案】B.

题型三：对数函数的定点问题 

13.对数函数的恒过定点为　　．

【解答】解：令，求得，，故函数所过定点是，

故答案为：．

14．若函数是幂函数，则函数（其中且的图象过定点　　

A． B． C． D．

【解答】解：因为函数是幂函数，所以，解得，所以函数中，令，解得，所以，所以的图象过定点．

故选：．

15.（炎德联考）若幂函数的图象经过函数且图象上的定点，则　　．

【解答】解：由，解得：，此时，即，设，则，解得：，故，故，

故答案为：4．

题型四：对数函数的图像

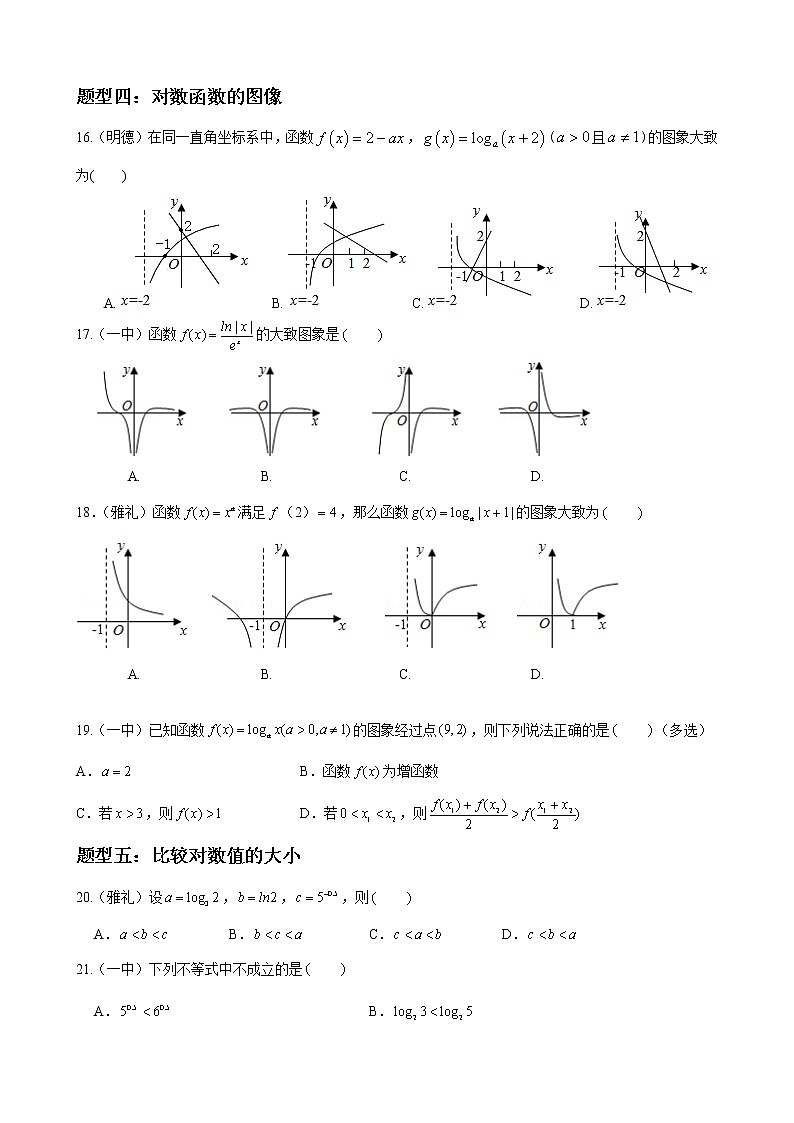
16.（明德）在同一直角坐标系中，函数，(且)的图象大致为(    )

A. B. C. D.

【解答】解：且，为减函数，排除；

若，则在上单调递增，此时的斜率为，排除；

若，则在上单调递减，此时的斜率为，排除；

故选：．

17.（一中）函数的大致图象是　　

A.                 B.                  C.                 D.

【解答】解：函数的定义域为，，；

当时，，，

当时，，

故选：．

18．（雅礼）函数满足（2），那么函数的图象大致为　　

A.                 B.                  C.                 D.

【解答】解：函数满足（2），可得．

函数关于对称，所以函数的图象为：

故选：．

19.（一中）已知函数的图象经过点，则下列说法正确的是　　（多选）

A．                     B．函数为增函数 

C．若，则         D．若，则

【解答】解：由题意知，，解得，所以，所以函数为增函数，故错误．正确．当时，，所以，故正确．

因为，，

所以，

又，所以，所以，所以，即，

故错误，

故选：．

题型五：比较对数值的大小

20.（雅礼）设，，，则　　

A． B． C． D．

【解答】解：，，，即．又，．

．综上可知：．

故选：．

21.（一中）下列不等式中不成立的是　　

A． B． 

C． D．

【解答】解：．函数在上单调递增，（5）（6），即，故正确；

．在上单调递增，（3）（5），即，故正确；

．，，，故正确；

．函数在上单调递减，，即，故错误．

故选：．

22.（雅礼）设，，，则　　

A． B． C． D．

【解答】解：；；；；又，；．故选：．

23.（明德）已知，，，则，，的大小关系是　　

A． B． C． D．

【解答】解：，，．故选：．

24.（长郡）下列大小关系，正确的是(   )

A. B. C. D.

25.下列大小关系，正确的是　　

A． B． 

C． D．

【解答】解：对于：考察指数函数，由于，故它在上是减函数，

， 故错；

对于：考察对数函数，由于，故它在上是增函数，

，而，

故正确；

对于：考察幂函数，由于，故它在上是增函数，

，故错；

对于：考考察指数函数，由于，故它在上是增函数，

，

考考察指数函数，由于，故它在上是减函数，

，故故错；

故选：．

26.（明德）三个数，，的大小关系为　　

A． B． 

C． D．

【解答】解：由三个数：，，，

可得大小关系为：，

故选：．

27.（明德）已知，则　　

A． B． C． D．3

【解答】解：．

故选：．

题型六：对数函数的单调性与值域

28.（广益）下列函数中，其定义域和值域与函数的定义域和值域相同的是　　

A． B． C． D．

【解答】解：由题意，函数，定义域为：，值域．

对于，定义域为，不对．

对于，定义域为：，值域为，不对．

对于，定义域为：，值域为，对．

对于，定义域为，值域，不对．

故选：．

29．（雅礼）函数的单调递增区间是　　

A． B． C． D．

【解答】解：由得或，

设，则当时，为增函数，此时为增函数，则为增函数，

即的单调递增区间为，

故选：．

30.（炎德联考）已知函数在上单调递增，则的取值范围是　　

A． B．， C． D．，

【解答】解：由，得或．令，

外层函数是其定义域内的增函数，要使函数在上单调递增，

则需内层函数在上单调递增且恒大于0，则，，，即．

的取值范围是，．

故选：．

31.（明德）已知函数是上的增函数，则实数的取值范围是(    )

A.    B.     C.    D.

【解答】解：由已知可得函数是上的单调递增函数，

则只需满足：，解得，

所以实数的取值范围为：，，

故选：．

32.（一中）下列函数中，最小值是的是(   )（多选）

A.       B.

C.     D.

【解答】解：由基本不等式的前提条件要求可得满足条件的选项是A、C；由取等号要求可知D选项不成立，

故选：AC．

33.（雅礼）下列结论正确的是(   )（多选）

A.，      B.若，则

C.若，则  D.若，，，则

【解答】解：对于，当时，，故错；

对于，当时，，则，故正确；

对于，若，则，则，故错；

对于，若，，，则有，故正确．

故选：．

34．（雅礼）给出下列结论，其中正确的结论是　　

A．函数的最大值为 

B．已知函数且在上是减函数，则实数的取值范围是， 

C．在同一平面直角坐标系中，函数与的图象关于直线对称 

D．若，则的值为1

【解答】解：对于：函数的最小值为，故错误；

对于：已知函数且在上是减函数，

所以，解得，当时，成立，

实数的取值范围是，，故正确；

对于：同一平面直角坐标系中，由于函数与互为反函数，

所以他们的图象关于直线对称，故正确；

对于：由于，则，则，同理，

所以，故正确．

故选：．

35.(一中)已知集合，.

(1)求集合、；(2)求.

【解析】(1)，，；

(2)，，，，

36.（长郡）已知函数(且)的图象过点.

(1)求函数的解析式；

(2)解不等式.

【解析】(1)因为函数(且)的图象过点.∴，

所以，即；

(2)因为单调递增，所以，即不等式的解集是.

37.(地质中学)已知函数.

(1)求关于的不等式的解集；

(2)若不等式对任意实数恒成立，求实数的取值范围.

【解析】(1)①当时，则由得：，即定义域为，

又为上的增函数，∴，∴当时，的解集为

②当时，则由得：，即定义域为，

又为上的增函数，∴，∴当时，的解集为，综上所述：当时，不等式解集为，当时，不等式解集为

(2)当时，，设，

设，，∴，∴，

∴，∵对任意实数恒成立，

∴，即实数的取值范围为。

38.（明德）已知函数，(且)，设.

(1)求函数的定义域；

(2)当时，求的取值范围.

【解析】(1)依题意得，所以的定义域为.

(2).即，当时，，

∴，当时，，∴.

39．（雅礼）已知函数．

（1）解关于的方程；

（2）若函数在上的最小值为2，求的值．

【解析】(1)将代入得，

∴(平方差)∴或，∴或

∴或(舍)，∴

(2)，∴

，令，，

令，∴，

∴，

①若，则，∴，(舍)，∴；

②若时，舍；

③若时，；∴

综上：或。

题型七：对数函数的应用题

40.（一中）我们处在一个有声世界里，不同场合，人们对声音的音量会有不同要求，音量大小的单位是分贝，对于一个强度为的声波，其音量的大小可由如下公式计算：，（其中是人耳能听到的声音的最低声波强度），则的声音强度是的声音强度的　　

A．倍 B．倍 C．10倍 D．倍

【解答】解：由题意，令，解得，，令，解得，，

两式作比得：，的声音强度是的声音强度的10倍．

故选：．

41.(明德)年是不平凡的一年，经历过短暂的网课学习后，同学们回到校园开始了正常的学习生活.为提高学生的学习效率，某心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数与听课时间之间的关系满足如图所示的曲线.当时，曲线是二次函数图象的一部分，其顶点为，当时，曲线是函数，(且)图象的一部分.根据专家研究，当注意力指数时听课效果最佳.

(1)试求的函数关系式；

(2)一道数学难题，讲解需要分钟，问老师能否经过合理安排在学生听课效果最佳时讲完？请说明理由.

【解析】(1)当时，设，将点代入得，

∴当时，；

当时，将点代入，得.

所以；

(2)当时，，解得，

所以；当时，，解得，

所以，综上时学生听课效果最佳，

此时，

答：教师能够合理安排时间讲完题目.

42.20世纪30年代，里克特．．制定了一种表明地震能量大小的尺度，就是使用测震仪衡量地震能量的等级，地震能量越大，测震仪记录的地震曲线的振幅就越大．这就是我们常说的里氏震级，其计算公式为：，其中，是被测地震的最大振幅，是“标准地震”的振幅（使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差）．

（1）假设在一次地震中，一个距离震中100千米的测震仪记录的地震最大振幅是20，此时标准地震的振幅是0.001，计算这次地震的震级（精确到；

（2）5级地震给人的震感已比较明显，计算8级地震的最大振幅是5级地震的最大振幅的多少倍？

（以下数据供参考：，

【解答】解：（1）

因此，这次地震的震级为里氏4.3级．

（2）由可得，即，．

当时，地震的最大振幅为；当时，地震的最大振幅为；

所以，两次地震的最大振幅之比是：

答：8级地震的最大振幅是5级地震的最大振幅的1000倍．

声明：试题解析著作权属所有，未经书面同意，不得复制发布

日期：2021/11/2 13:41题型八：对数函数与奇偶性的综合题

43.（师大）已知函数是偶函数，且当时，(，且).

(1)求当时的的解析式；

(2)在①在上单调递增；②在区间上恒有这两个条件中任选一个补充到本题中，求的取值范围.

(注；如果选择多个条件分别解答，则按第一个解答计分)

【解析】(1)当时，，又是偶函数，即，

即，；

(2)，此时的取值范围是，

选条件②的解析：若，则，显然不合要求，

当时，，而与都是偶函数，则只需考虑即可，

此时是单调递减的，而是单调递增的，则，

此时的取值范围是.
44.(师大)已知函数是奇函数.

(1)求的值，判断的单调性并用定义证明之；

(2)解不等式：.

【解析】(1)显然函数的定义域是，据题意有，得，即

此时满足题意

，由此可判断出是上的递增函数

以下用定义证明：，且，则

所以

即，故是上的递增函数.

(2)由得或

即：或或或

即解集为

45.（一中）已知，且是定义在上的奇函数，当时，.

(1)若在上的最大值是，求实数的值；

(2)当时，若对任意，，恒有，求的取值范围.

【解析】(1)且，，对称轴为，

，，，∴；

(2)，

，∴

而，令，

当且仅当时取等，∴，

，∴。

46.（明德）设函数(且)是定义域为的奇函数.

(1)求的值；

(2)若，求使不等式对一切恒成立的实数的取值范围；

(3)若函数的图象过点，是否存在正数，使函数在上的最大值为，若存在，求出的值；若不存在，请说明理由.

【解析】(1)是定义域为的奇函数，

∴，.经验证此时(且)为奇函数，∴

(2)由(1)得，由得又.∴

由得.

∴为奇函数.∴，∴，∴为上的增函数，

∴对一切恒成立，即对一切恒成立，

故，解得

(3)假设存在正数符合意，由得

，设，

则，∵，

∴，记，

∵函数在上的最大位为，

(ⅰ)若，则函数在有最小值为，∵对称轴，

∴，不合题意；

(ⅱ)若，则函数在上恒成立，且最大值为，小值大于，

①，又此时，又，

故意义，所以应舍去；

②无解，

故不存在正数，使函数在上的最大值为.

题型九：与对数函数有关的恒成立问题

47.(炎德联考)已知函数图象过点.

(1)当时，恒成立，求实数的取值范围；

(2)若关于的方程在上有解，求的取值范围.

【解析】(1)由题可知，所以，，所以.

当时，恒成立，即，

∴在恒成立，由于是减函数，

故当时函数取到最大值，∴，即实数的取值范围是.

(2)令，在上单调递减，又单调递减.

所以在上是增函数，在上是减函数，

∴只需要，即可保证关于的方程在在上有解，下解此不等式组.代入函数解析式得，

解得，

即当时关于的方程在上有解.

48.(师大)已知，．

（1）求的解析式；

（2）求的值域；

（3）设，时，对任意，，总有成立，求的取值范围．

【解答】解：（1）令，则，

故．

，

（2）再设，则，，

①当时，，在上是减函数，其值域为；

②当时，的对称轴，

故其在上是减函数，在，上是增函数．其值域为，；

③当时，的对称轴，

故其在上是减函数．其值域为；

（3）对任意，，总有成立，等价于在，内满足其最大值与最小值的差小于等于．

又，

令，，，

①当时，在，单调递增，

函数在，内的最大值是（2），最小值是．

，可得．不满足，舍去．

②当时，，所以在在，单调递增，

同①可得符合题意．

③当时，在，单调递减，函数在，内的最小值是（2），最大值是．

，解得，与矛盾，舍去．

④当时，函数在，递减，在，递增，

，

故只需即可，

，

综上所述，的取值范围为，．

49.(明德)已知，函数.

(1)当时，解不等式；

(2)若关于的方程有两个不等的实数根，求的取值范围；

(3)设，若对任意，函数在区上的最大值与最小值的差不超过，求的取值范围.

【解析】(1)当时，，由得，

∴得，即，解得或，

∴当时，不等式的解集为

(2)由题意得，该问题等价于，化简得，

即

①当时，，不合题意，舍去.

②当时，，不合题意，舍去.

③当且时，，且.由，得(且)；

由，得(且)；

依题意，若原方程由两个不等的实数根，则(且).

故所求的取值范围为.

(3)易得，当时，在上单调递减.

故函数在区间上的最大值与最小值分别为，.

则对恒成立，即，

对任意恒成立.因为，函数的对称轴，

函数在区间上单调递增，故时，有最小值，

∴，得故所求的取值范围为.