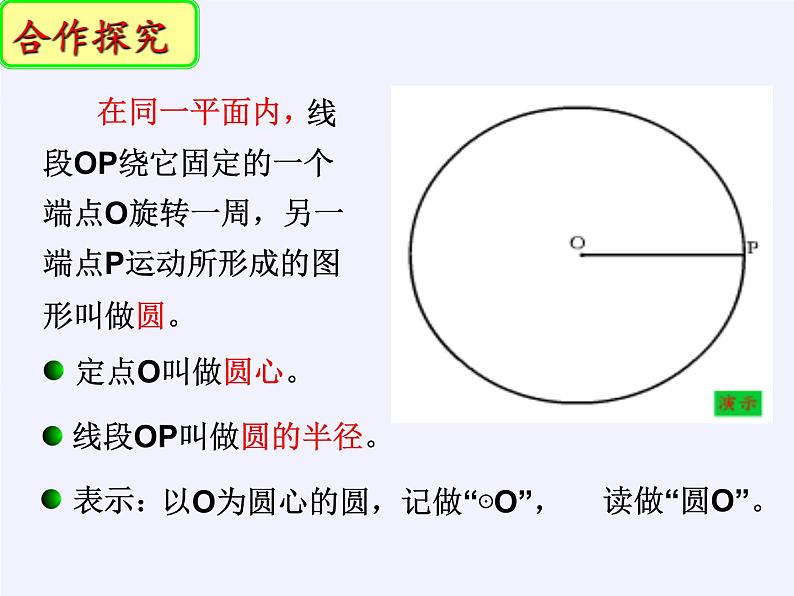
初中数学苏科版九年级上册第2章 对称图形——圆2.1 圆授课ppt课件

这是一份初中数学苏科版九年级上册第2章 对称图形——圆2.1 圆授课ppt课件，共19页。PPT课件主要包含了一石激起千层浪，乐在其中，图片欣赏，奥运五环，福建土楼，小憩片刻，合作探究，归纳小结，OA＜r，OBr等内容，欢迎下载使用。

问题：以上这些图片，给我们展示了一个怎样的数学图形？
1.要确定一个圆,必须确定圆的____和____
圆心确定圆的位置,半径确定圆的大小.
2.如何画圆，数学上画圆一般用什么工具？
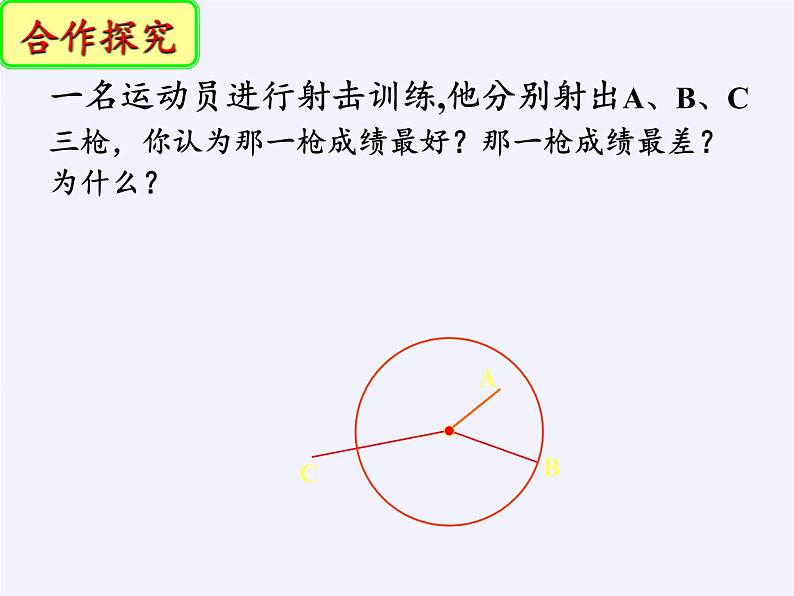
一名运动员进行射击训练,他分别射出A、B、C三枪，你认为那一枪成绩最好？那一枪成绩最差？为什么？
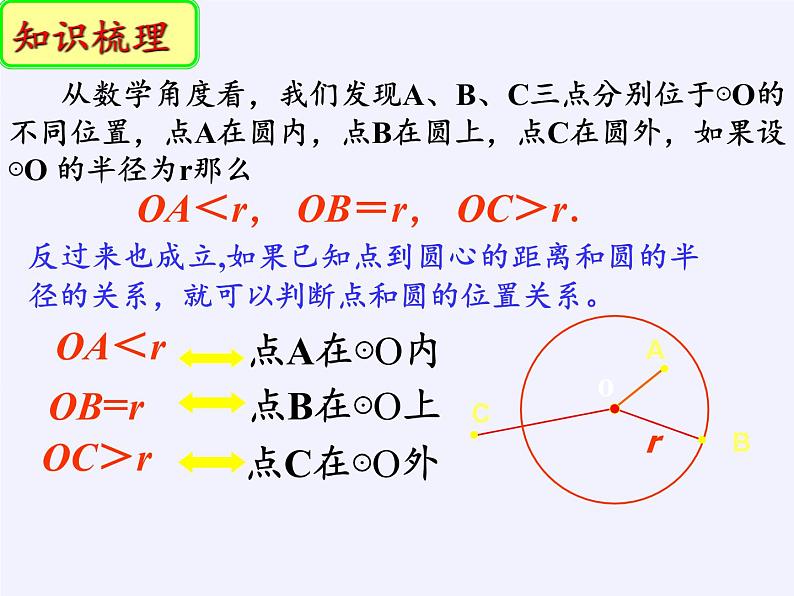
从数学角度看，我们发现A、B、C三点分别位于⊙O的不同位置，点A在圆内，点B在圆上，点C在圆外，如果设⊙O 的半径为r那么
点A在⊙O内
点B在⊙O上
点C在⊙O外
OA＜r， OB＝r， OC＞r．
反过来也成立,如果已知点到圆心的距离和圆的半径的关系，就可以判断点和圆的位置关系。
如果⊙O的半径为r，点P到圆心的距离为d，那么点P在圆内 d＜r点P在圆上 d＝r点P在圆外 d＞r
平面上的一个圆，把平面上的点分成三类：圆上的点，圆内的点和圆外的点。
思考：平面上的一个圆把平面上的点分成哪几部分？
问：圆上的点有什么特征？圆内的点、圆外的点又有什么特征？
圆上各点到圆心(定点)的距离都等于半径(定长);到圆心距离等于半径的点都在圆上.也就是说:圆是到定点距离等于定长的点的集合.
圆内各点到圆心的距离都小于半径;到圆心 距离小于半径的点都在圆内.也就是说:圆的内部可以看作是到圆心距离小于半径的点的集合.
圆外的点到圆心的距离都大于半径;到圆心距离大于半径的点都在圆外.也就是说:圆的外部可以看作是到圆心距离大于半径的点的集合.
如图，已知点A，请作出到点A的距离等于2cm的点的集合．（1）这个圆的外部是满足什么条件的点的集合？（2）请用阴影表示出到点A的距离小于或等于2cm的点的集合．
如图，已知点A、B，且AB＝4cm.（1）画出下列图形： 到点A的距离等于2cm的点的集合； 到点B的距离等于3cm的点的集合．（2）在所画图中，到点A的距离等于2cm，且到点B的距离等于3cm的点有几个？请在图中将它们表示出来．（3）在所画图中，到点A的距离小于或等于2cm，且到点B的距离大于或等于3cm的点的集合是怎样的图形？把它表示出来．
例1　已知⊙O的半径为4cm，如果点P到圆心O的距离为4.5cm，那么点P与⊙O有怎样的位置关系？如果点P到圆心O的距离为4cm、3cm呢？
如何判断点与圆的位置关系？ 只需要比较点到圆心的距离d与半径r的大小关系.
设⊙O的半径为rcm，点P到圆心O的距离为dcm．
由题意得，r＝4cm．
当d＝4.5cm时，∵ d＞r，∴点P在⊙O外．
当d＝4cm时，∵ d＝r，∴点P在⊙O上．
当d＝3cm时，∵ d＜r，∴点P在⊙O内．
例2.如图已知矩形ABCD的边AB=3厘米，AD=4厘米
（1）以点A为圆心，3厘米为半径作圆A，则点B、C、D与圆A的位置关系如何？
（2）以点A为圆心，r为半径作圆A，使B、C、D三点中至少有一个点在圆内。求r的取值范围。
（3）以点A为圆心，r为半径作圆A，使B、C、D三点中在圆内和在圆外都至少有一个点，求r的取值范围
例3.已知：如图，BD、CE是ABC的高，M是BC的中点。试问：点B、C、D、E在以点M为圆心的圆上吗？
1.矩形ABCD的对角线AC、BD相交于点O，点A、B、C、D是否在以点O为圆心的同一个圆上？为什么？2.如果E、F、G、H分别为OA、OB、OC、OD的中点，点E、F、G、H在同一个圆上？为什么？
通过本课的学习，你又有什么获？