数学八年级下册19.2.2 一次函数教学课件ppt

这是一份数学八年级下册19.2.2 一次函数教学课件ppt，共22页。PPT课件主要包含了教材的地位与作用，一教材分析，教材的重点与难点，二教学目标，铺垫孕孵作好衔接，应用知识解决问题，讨论交流探索新知，深入探究掌握新知，创设情境引入新课，归纳反思布置作业等内容，欢迎下载使用。

分段函数是一类特殊的函数,有着广泛的应用,教材中只以例题形式出现,并未作深入地系统介绍,但分段函数与一般函数有明显的区别,学习时往往受一般函数的影响而产生负迁移,不少学生对它认识肤浅模糊。本节课的主要内容是从函数的观点来认识：分段函数是刻画现实世界数量关系的数学模型。通过本节课的学习使学生在函数建模及其应用类问题中认识到，关键是要审清题意，依据题目所给的条件，合理选择适当的方法，从而列出函数解析式求解问题。加强知识间的横向和纵向联系，发挥函数的统领作用，构建和发展相互联系的知识体系。进一步体验函数的重要性，提高灵活分析问题和解决问题的能力。
“探索具体问题中的数量关系和变化规律，并能运用函数进行描述和解决问题”，这是《新课标》关于函数目标的一段描述。因此，“函数建模及其应用”类试题，在全国各地中考试卷中备受青睐。而建模的首要是建立函数关系式。因此本节教学重点：１．确定一次函数解析式。建立函数模型解决实际问题。２．灵活运用知识解决相关问题。教学难点：对数形结合思想的领会，提升分析解决问题的能力。
1.了解一次分段函数的概念。 2.掌握如何求分段函数解析式，会根据题意求出分段函数的解析式并画出函数图象。
通过对分段函数图象和解析式的探究及相关实际问题的解决, 体会分类讨论思想的应用。
体验数形结合，逐步学习利用这一思想分析解决问题。
１．积极参与活动，提高学习兴趣。２．养成实事求是、具体问题具体分析的习惯。
学法指导：引导学生观察，合作学习，归纳、总结等，使学生真正成为学习的主体。
教法选择：１、动－－引导学生动口说，动脑想，动手做，亲身经历知识发生发展的过程。２、探－－引导学生动手画图，合作讨论，通过探究学习激发强烈的探索欲望。３、渗－－在整个教学过程中，渗透用联系的观点看待数学问题的辩证思想。４、乐－－本节课的设计力求做到与学生的生活实际联系紧一点，直观多一点，动手多一点，使学生兴趣高一点，自信心强一点，使学生乐于学习、乐于思考。
三、学法指导与教法选择
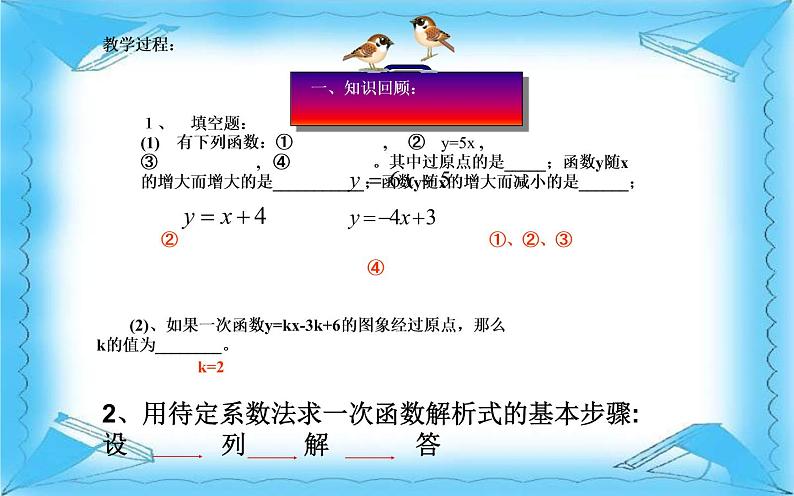
１、　填空题：(1)　有下列函数：①　　　　　 , ②　y=5x ,③　　　 , ④ 。其中过原点的是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；
　　(2)、如果一次函数y=kx-3k+6的图象经过原点，那么k的值为________。　
2、用待定系数法求一次函数解析式的基本步骤:设 列 解 答
3.能综合利用分段函数解析式与图象分析并解决实际问题。
2. 掌握如何求分段函数解析式，会画分段函数图象，并能灵活运用。
1.了解分段函数的概念。
小亮在超市的糖果柜台看见某种糖果特价：该糖果的价格为5元／千克，如果一次购买2千克以上，超过2千克部分的糖果的价格打8折，请帮他完成下面问题：（1）填写下表：
2.5 5 7.5 1012 14 16 18 ……
思考:⑴付款金额随购买糖果数量变化的规律是否一直不变？若不是，该怎样分？分成几段？购买糖果数量的相应范围是多少？ ⑵函数解析式是否应相应地写出几个？函数图象是几部分呢？
（2）写出付款金额与购买糖果数量之间的函数解析式，并画出函数图象。
解：（2）设购买该糖果数量为x千克，付款金额为y元。当0≤x≤2时，y ＝5x当x＞2时，y＝5× 0.8× (x－2)＋10＝4x＋2函数图象如图：
当0≤x≤2时，y ＝5x当x＞2时，y＝ 5× 0.8× (x－2)＋10＝4x＋2
解：（2）设购买该糖果数量为x千克，付款金额为y元。函数图象如图：
要注意： (1)写分段函数解析式时，自变量的取值范围写在相应函数解析式的后面。 (2) 分段函数是一个函数。（3）函数在自变量不同的范围内解析式（或函数图象）不同。
三、例：一进水的容器，从开始4分钟只进水较大，随后8分钟内进水减弱，容器的水量y（升）与时间x（分）关系如图。（1）求当0≤x≤4时，y与x的函数关系式（2）求当4＜x≤12时，y与x的函数关系式
分析:从函数图象上看图象分为两段,当0≤x≤4时, y与x是正比例函数; 4＜x≤12时,y是x的一次函数,且函数图象经过点(4,20)和(12,30),设出相应的函数关系式,将点的坐标代入即可确定函数关系式,根据函数关系式可解决问题.
例：一进水的容器，从开始4分钟只进水较大，随后8分钟内进水减弱，容器的水量y（升）与时间x（分）关系如图.
解：（1）设当0≤x≤4时， y与x的函数关系式为y=k1x
∵函数图象过点（4，20）
∴ 20=4k1, 得k1=5
∴y=5x( 0≤x≤4)
例：一进水的容器，从开始4分钟只进水较大，随后8分钟内进水减弱，容器的水量y（升）与时间x（分）关系如图
解：（2）设4＜x≤12时， y与x的函数关系式为y=k2x+b
∵图象过点（4，20），（12，30），于是：
20=4k2+b 30=12k2+b
解得: k2= b=15
∴y= x+15 (4＜x≤12)
1、由实际问题列出二元一次方程，再转化为函数解析式。 2、用待定系数法求函数解析式。☻画分段函数图象的步骤：①明确函数解析式分几段，以及对应的自变量取值范围是什么，解析式分别是什么；②选取每一段自变量取值范围端点数值（或特殊值），分别代入对应的解析式计算对应的函数值，得到点的坐标；③描点；④连线。
☻求函数解析式的方法主要有两种：
☻分段函数中函数自变量的取值范围不同，所对应的函数关系(图象)也不相同。
1、 某工厂月产量y件与月份x（月）的函数图象如图，则下列说法正确的是 〖 〗 (A)1月至3月每月产量逐月增加, 4、5两月每月产量逐月减少； (B)1月至3月每月产量逐月增加, 4、5两月每月产量与3月持平； (C)1月至3月每月产量逐月增加, 4、5两月均停止生产； (D)1月至3月每月产量不变, 4、5两月均停止生产.
2、图中折线表示超市冷藏室在0：00～4：00的温度m（单位： ℃）随时间t（单位：时）的变化情况：下列对该冷藏室的温度描述正确的是（ ）（A）0：00～2：00温度升高快， 2：00～4：00温度升高慢；（B）0：00～2：00温度升高慢， 2：00～4：00温度升高快；（C）0：00～2：00保持6 ℃ 恒温，2：00～4：00保持10 ℃ 恒温；（D）0：00～2：00保持6 ℃ 恒温，2：00～4：00匀速升温，每小时升高2 ℃ ；
3、某市出租车５千米内起步价为８元，以后每增加１千米加价１元。
(2)请写出乘坐出租车费用y元与路程ｘ千米的函数关系式.
课堂巩固练习：
4、某移动公司采用分段计费的方法来计算话费,月通话时间（分钟）与相应话费（元）之间的函数图象如图所示：（１）月通话为100分钟时，应交话费　　元；（２）当x>100时，求y与x之间的函数关系式；（3）月通话为280分钟时，应交话费多少元？
解：（1）观察图象可知月通话为100分钟时，应交话费40元；
（2） 设x>100时， y与x之间的函数关系式为y=kx+b由图可知：x=100时,y=40；x=200时y=60则有 　 , 解之得:所求函数关系式为:
（3）把x=280代入关系式 得:y=76　即月通话为280分钟时，应交话费76元．
1、本节课我们学习了哪些知识？ 2、学完本节课后，我的最大收获是什么？ 3、我认为在什么地方还理解不透？
1.书： P119 练习， P129 习题14.3第10题 2.选做：书： P121习题14.2第12题要求：抄题、写过程