人教版八年级下册19.2.2 一次函数评优课复习课件ppt

这是一份人教版八年级下册19.2.2 一次函数评优课复习课件ppt，共23页。PPT课件主要包含了情景引入，-2x+y0，y2x，-2x+y1，y2x+1，题型一，一次函数函数的概念，考题分类，题型二，题型三等内容，欢迎下载使用。

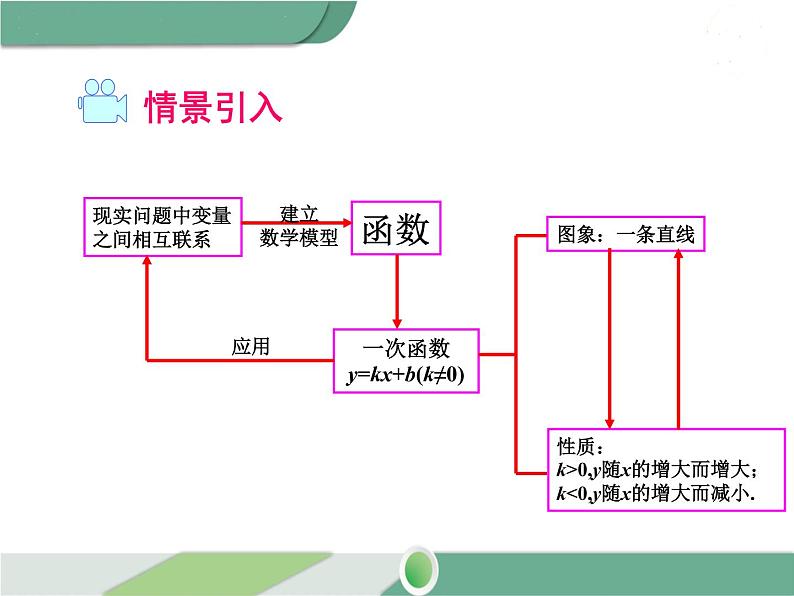
现实问题中变量之间相互联系
一次函数y=kx+b(k≠0)
性质：k>0,y随x的增大而增大；k<0,y随x的增大而减小.
2. 一次函数y＝x+2的图象不经过 (　　)　　　　　　　　　　　　　　　　　　　　 A．第一象限 B．第二象限 C．第三象限 D．第四象限
【例 2】 如果点P1（3，y1），P2（2，y2）在一次函数y=x－1的图象上，则y1 y2．（填“＞”，“＜”或“=”）
1．一次函数y＝－2x＋4的图象与y轴的交点坐标是 (　　) A. (0，4) B．(4，0) C．(2，0) D．(0，2)
一次函数解析式中k、b 对图象及性质的影响
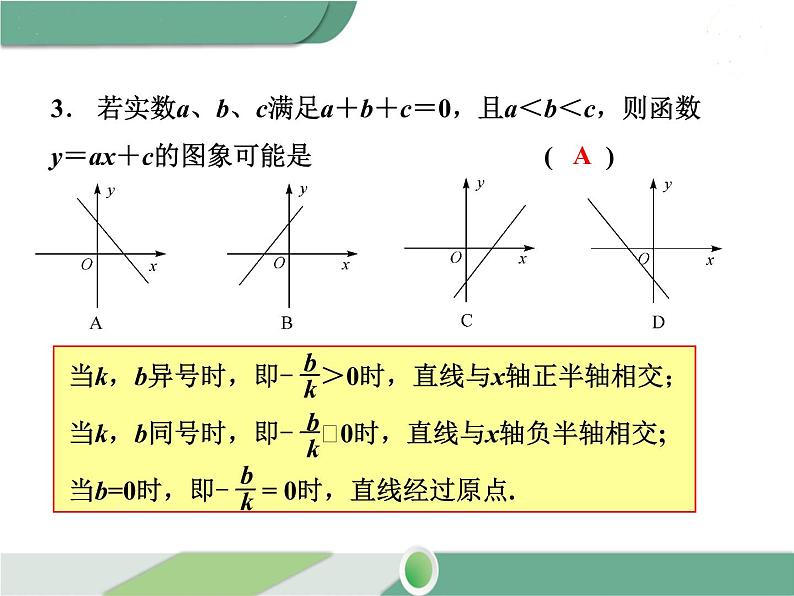
3． 若实数a、b、c满足a＋b＋c＝0，且a＜b＜c，则函数y＝ax＋c的图象可能是 (　　)
待定系数法求一次函数的解析式
【例 3】　如图，直线l1、l2相交于点A(2，3)，直线l1与x轴的交点坐标为(－1，0)，直线l2与y轴的交点坐标为(0，－2)，求直线l1、l2的解析式；
对应训练: 一次函数的图象过点(0,2)，且函数y的值随自变量x的增大而增大，请写出一个符合条件的函数解析式 __________________________ ．
y＝x＋2 （只需k>0即可）
(2)若直线y＝－x＋b与x轴交于点(2，0)，则关于x的不等式－x＋b>0的解集是________．
【例 4】　(1)已知一次函数y＝ax＋b(a≠0)中，x、y的部分对应值如下表，那么关于x的方程ax＋b＝0的解是________.
一次函数与一次方程、一次不等式问题
对应训练: 在平面直角坐标系中，直线y＝kx＋3经过点(－1，1)，求不等式kx＋3＜0的解集．
1. 将直线y=2x向上平移1个单位长度后得到的直线是　 　．
一次函数图象与图形变换及面积
2.M是OB上的一点，如图所示，若△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的解析式为 ______.
3. 如图所示,已知直线y=2x+3与直线y=-2x-1相交于点C (1)求两直线交点C的坐标; (2)求△ABC的面积.
参考答案：（1）交点C的坐标是（-1，1）;（2）△ABC的面积是2.
如图，直线OC、BC的函数关系式分别为y=x和 y=-2x+6，动点P（a, 0）在OB上移动0< a<3），过点P作直线与x轴垂直．
（2）设△OBC中位于直线l左侧部分的面积为S,写出S与 a 之间的函数关系式；（3）当a为何值时，直线平分△BOC的面积?
（1）点C的坐标是（2，2）
（2）设△OBC中位于直线l左侧部分的面积为S,写出S与 a 之间的函数关系式；
（3）当a为何值时，直线平分△BOC的面积?
2.一次函数的图象与性质
3.一次函数解析式的确定
4.一次函数与方程(组)、不等式的关系
5.一次函数的综合应用
1.填空题：（1）有下列函数：①y=6x-5, ②y=5x, ③y=x+4, ④y=-4x+3.其中过原点的直线是 ；函数y随x的增大而增大的是 ；函数y随x的增大而减小的是 ；图象过第一、二、三象限的是 .
2.直线y=3x+6与坐标轴围成的三角形的面积是_________.
3.直线y=kx+b与y=3x平行，且过（1，2），则k= ,b= .
4.一次函数y=ax+b,若a+b=0,则它的图象必过点_________.
5.根据下列一次函数y=kx+b(k≠0)草图回答出各图中k、b的符号：
k 0 ,b 0.
k 0 ,b 0.
k 0 ,b___0.
6.函数 中自变量x的取值范围是 .
7.下列各点中，在函数y=2x-7的图象上的是（ ） A.(2,3) B.(3,1) C.(0,-7) D.(-1,9)
8.已知一次函数y=kx-k,若y随x的增大而减小，则该函数的图象经过（ ）A.第一、二、三象限 B.第一、二、四象限C.第二、三、四象限 D.第一、三、四象限
9.一次函数y=kx+b中，kb>0,且y随x的增大而减小，则它的图象大致为（ ）
10.一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（ ）
11.已知函数y=3x+1,当自变量增加m时，相应的函数值增加（ ）