数学第十九章 一次函数综合与测试复习课件ppt

这是一份数学第十九章 一次函数综合与测试复习课件ppt，共24页。PPT课件主要包含了函数的概念，两点法，yx+1，平移法，y3x，y-x+8等内容，欢迎下载使用。

知识要点:1.函数,变量,常量;2.函数的三种表示法;3.正比例函数:定义,图象,性质;4.一次函数:定义,图象,性质;5.一次函数的应用.6.一次函数与一元一次方程,一元一次不等式,二元一次方程组的关系.
一.常量、变量： 在一个变化过程中,数值发生变化的量叫做 变量 ；数值始终不变的量叫做 常量 ；
函数的定义：一般的，在一个变化过程中,如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数．
三、函数中自变量取值范围的求法：
（1）.用整式表示的函数，自变量的取值范围是全体实数。（2）用分式表示的函数，自变量的取值范围是使分母不为0的一切实数。（3）用奇次根式表示的函数，自变量的取值范围是全体实数。 用偶次根式表示的函数，自变量的取值范围是使被开方数为非负数的一 切实数。（4）若解析式由上述几种形式综合而成，须先求出各部分的取值范围，然后再求其公共范围，即为自变量的取值范围。（5）对于与实际问题有关系的，自变量的取值范围应使实际问题有意义。
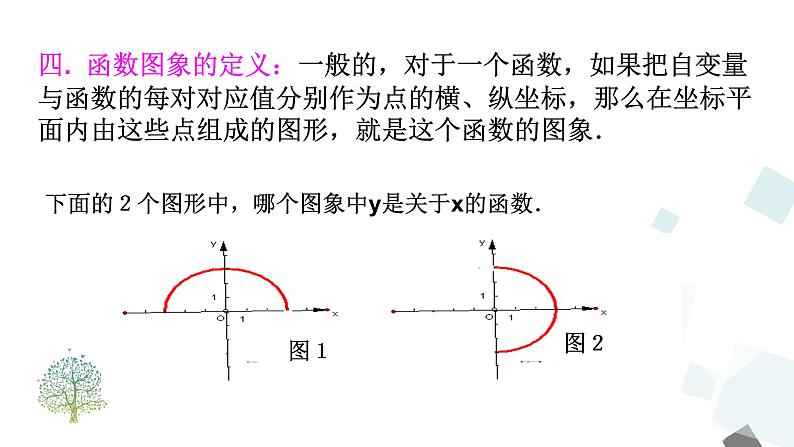
四. 函数图象的定义：一般的，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么在坐标平面内由这些点组成的图形，就是这个函数的图象．
下面的２个图形中，哪个图象中y是关于x的函数．
1、列表（表中给出一些自变量的值及其对应的函数值。）
2、描点：（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点。
3、连线：（按照横坐标由小到大的顺序把所描的各点用平滑的曲线连接起来）。
五、用描点法画函数的图象的一般步骤：
注意：列表时自变量由小到大，相差一样，有时需对称。
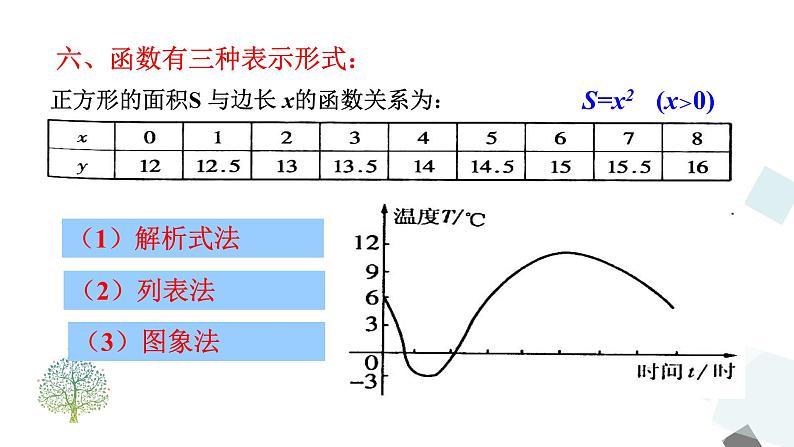
六、函数有三种表示形式：
七、正比例函数与一次函数的概念：
一般地，形如y=kx(k为常数，且k≠0)的函数叫做正比例函数.其中k叫做比例系数。
当b =0 时,y=kx+b 即为 y=kx,所以正比例函数，是一次函数的特例.
一般地，形如y=kx+b(k,b为常数，且k≠0)的函数叫做一次函数.
（1)图象:正比例函数y= kx (k 是常数，k≠0)) 的图象是经过原点的一条直线，我们称它为直线y= kx 。 (2)性质:当k>0时,直线y= kx经过第三，一象限，从左向右上升，即随着x的增大y也增大；当k<0时,直线y= kx经过二,四象限，从左向右下降，即随着 x的增大y反而减小。
八.正比例函数的图象与性质：
九、一次函数与正比例函数的图象与性质
１、图象是经过（０，０）与（１，k）的一条直线
２、当k>0时，图象过一、三象限；y随x的增大而增大。　　当k<0时，图象过二、四象限；y随x的增大而减少。
十.怎样画一次函数y=kx+b的图象？
先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法， －－待定系数法
十一、求函数解析式的方法:
十二.一次函数与一元一次方程：
　求ax+b=0(a，b是　常数，a≠0)的解．
x为何值时函数y= ax+b的值为0．
求ax+b=0(a, b是　常数，a≠0)的解．
求直线y= ax+b与 x 轴交点的横坐标．
十三.一次函数与一元一次不等式：
解不等式ax+b＞0(a，b是常数，a≠0) ．
　x为何值时　函数y= ax+b的值 大于0．
解不等式ax+b＞0(a，b是常数，a≠0) ．
求直线y= ax+b在 x轴上方的部分（射线）所对应的的横坐标的取值范围．
十四.一次函数与二元一次方程组：
自变量（x）为何值时两个函数的值相等．并求出这个函数值
确定两直线交点的坐标.
例1 （1）若y=5x3m-2是正比例函数，m= 。
１、直线y=kx+b经过一、二、四象限，则K 0, b 0．
此时，直线y=bx＋k的图象只能是( )
２、已知直线y=kx+b平行与直线y=-2x，且与y轴交于点（０，－２），则k=___,b=___.　此时，直线y=kx+b可以由直线y=-2x经过怎样平移得到？
３.若一次函数y=x+b的图象过点A（1，-1），则b=__________。
４.根据如图所示的条件，求直线的表达式。
５、柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克（1）写出余油量Q与时间t的函数关系式.
解：（１）设所求函数关系式为：Ｑ＝kt＋b。把t=0，Q=40；t=3.5，Q=22.5分别代入上式，得
解析式为：Q＝－５t+40　
取t=0，得Q=40；取t=８，得Q=０。描出点Ａ（０，40），B（8，0）。然后连成线段AB即是所求的图形。
注意：（1）求出函数关系式时，必须找出自变量的取值范围。（2）画函数图象时，应根据函数自变量的取值范围来确定图象的范围。
　５、柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克（1）写出余油量Q与时间t的函数关系式.
（2）画出这个函数的图象。
图象是包括两端点的线段
６、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。（1）服药后______时，血液中含药量最高，达到每毫升_______毫克，接着逐步衰弱。（2）服药5时，血液中含药量为每毫升____毫克。
６、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。（3）当x≤2时y与x之间的函数关系式是___________。（4）当x≥2时y与x之间的函数关系式是___________。（5）如果每毫升血液中含药量3毫克或3毫克以上时，治疗疾病最有效，那么这个有效时间是___时。