




- 24.1 测量 PPT课件 课件 8 次下载
- 24.2 直角三角形的性质 PPT课件 课件 10 次下载
- 24.3 第2课时 特殊角的三角函数值 PPT课件 课件 7 次下载
- 24.3 第3课时 用计算器求锐角三角函数值 PPT课件 课件 7 次下载
- 24.4 第1课时 解直角三角形及其简单应用 PPT课件 课件 7 次下载
华师大版九年级上册1.锐角三角函数优秀ppt课件
展开1.理解锐角三角函数的定义;(重点)2.掌握三角函数之间的关系并会计算.(难点)
1.在Rt△ABC中,∠C=90°,AB=10,BC=6,AC=______.2.在Rt△ABC中,∠C=90°,∠A=30°,AB=10cm,则BC= ,理由是 .
30°所对直角边是斜边的一半
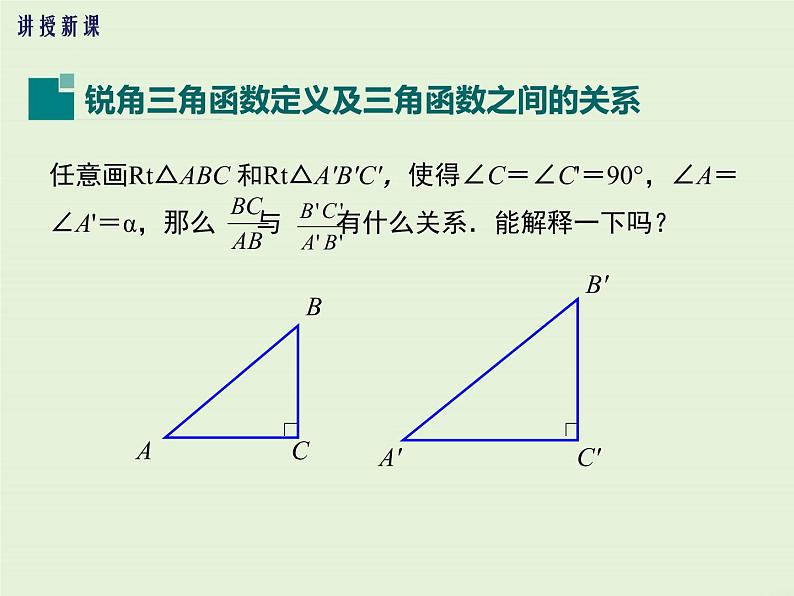
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么 与 有什么关系.能解释一下吗?
在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角∠A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值.
如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边与斜边的比叫做∠A的正弦(sine),记作sinA 即
例如,当∠A=30°时,我们有
当∠A=45°时,我们有
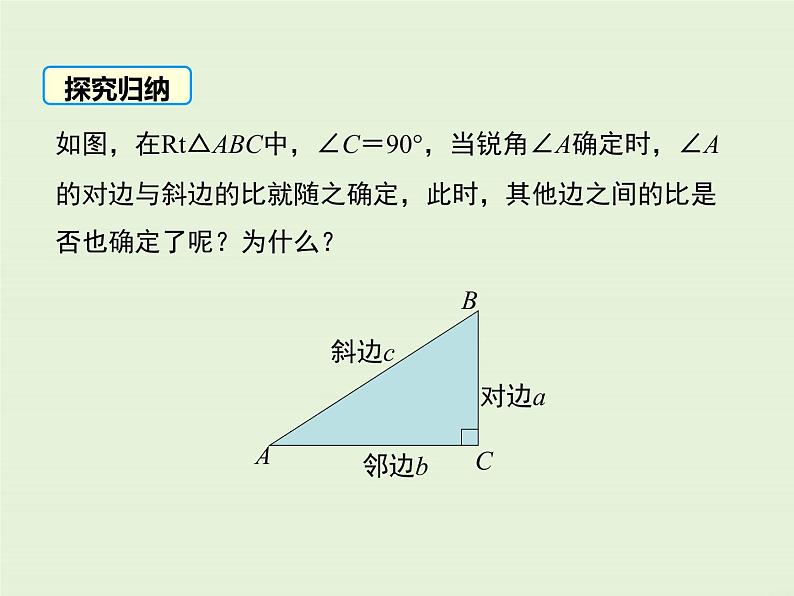
如图,在Rt△ABC中,∠C=90°,当锐角∠A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
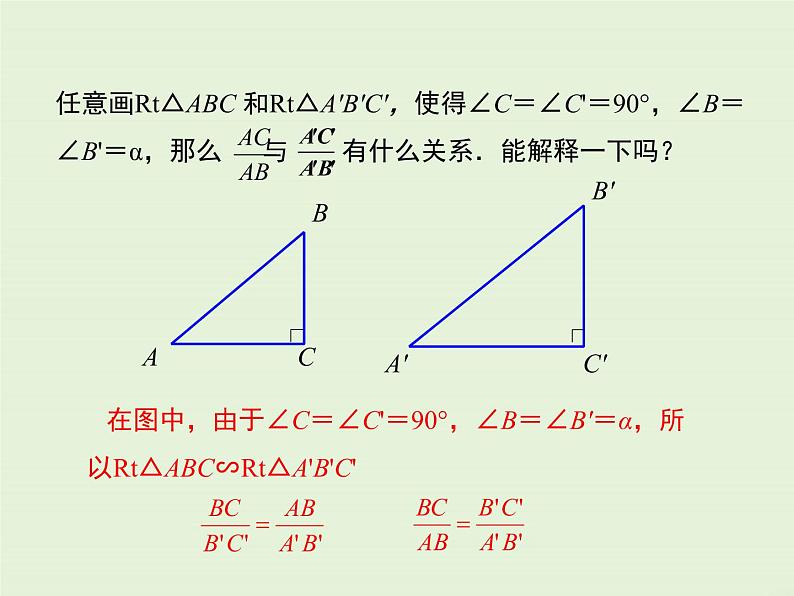
任意画Rt△ABC 和Rt△A'B'C',使得∠C=∠C'=90°,∠B=∠B'=α,那么 与 有什么关系.能解释一下吗?
在图中,由于∠C=∠C'=90°,∠B=∠B'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角∠B的度数一定时,不管三角形的大小如何,∠B的对边与斜边的比也是一个固定值.
当锐角∠B的大小确定时,∠B的邻边与斜边的比也是固定的,我们把∠B的邻边与斜边的比叫做∠B的余弦(csine),记作csB,即
1.sinA、csA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)、 csA是一个比值(数值)、 csA的大小只与∠A的大小有关,而与直角三角形的边长无关.
如图:在Rt △ABC中,∠C=90°,
当直角三角形的一个锐角的大小确定时,其对边与邻边比值也是唯一确定的吗?
在直角三角形中,当锐角∠A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值.
如图,Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,∠A=∠A′=α,问: 有什么关系?
由于∠C=∠C′=90°,∠A=∠A′=α,所以Rt△ABC ∽ Rt△A′B′C′
如图,在Rt △ABC中,∠C=90°,
我们把锐角A的对边与邻边的比叫做∠A的 正切,记作 tanA.
一个角的正切表示定值、比值、正值.
思考:锐角∠A的正切值可以等于1吗?为什么?可以大于1吗?
对于锐角∠A的每一个确定的值,tanA都有唯一的确定的值与它对应.
解:可以等于1,此时为等腰直角三角形;可以大于1.
1.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,图中sinB可由哪两条线段比求得.
解:在Rt△ABC中,
因为∠B=∠ACD,所以
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值.
2. 如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、csA、tanA的值.
3. 如图,在Rt△ABC中,∠C=90°,csA= ,求sinA、tanA的值.
设AC=15k,则AB=17k
4.下图中∠ACB=90°,CD⊥AB,垂足为D.完成下列填空.
5. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求:sinA、csB的值.
华师大版九年级上册1.锐角三角函数习题课件ppt: 这是一份华师大版九年级上册1.锐角三角函数习题课件ppt,共27页。PPT课件主要包含了正实数,∶4∶5等内容,欢迎下载使用。
初中数学华师大版九年级上册1.锐角三角函数课文课件ppt: 这是一份初中数学华师大版九年级上册1.锐角三角函数课文课件ppt,共9页。PPT课件主要包含了解02815,解07951,解03191,解47°10,解77°25′,解74°50′等内容,欢迎下载使用。
2021学年1.锐角三角函数评课ppt课件: 这是一份2021学年1.锐角三角函数评课ppt课件,共14页。













