人教版（2024）六年级下册5 数学广角 （鸽巢问题）完美版ppt课件

这是一份人教版（2024）六年级下册5 数学广角 （鸽巢问题）完美版ppt课件，文件包含2鸽巢问题2pptx、媒体1mp4、媒体2mp4等3份课件配套教学资源，其中PPT共41页， 欢迎下载使用。
一、上节课我们学了什么？
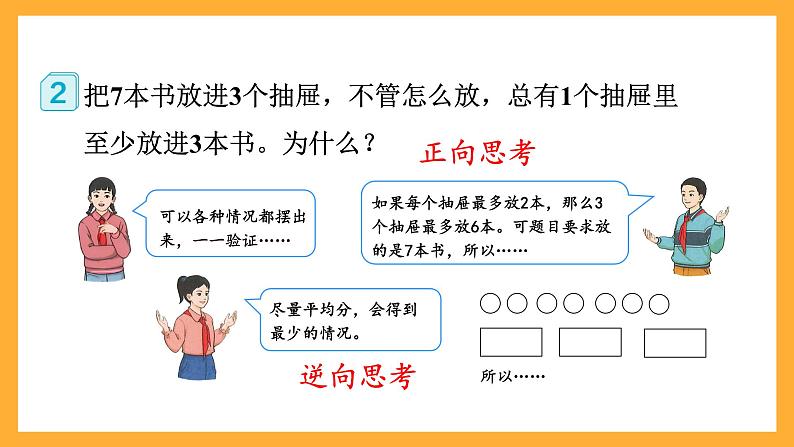
尽量平均分，会得到最少的情况。
把7本书放进3个抽屉，不管怎么放，总有1个抽屉里至少放进3本书。为什么？
如果有8本书，会怎样呢？10本书呢？
7 ÷ 3 = 2（本）······1（本）
2 + 1 = 3（本）
8 ÷ 3 = 2（本）······2（本）
10÷ 3 =3（本）······1（本）
3 + 1 = 4（本）
张叔叔参加飞镖比赛，投了5镖，成绩是41环。张叔叔至少有一镖不低于9环。为什么？
假设每镖都不超过8环，投了5镖，最多40环。可是题目说成绩是41环，所以假设不成立，至少有一镖不低于9环。
41 ÷ 5 = 8(环)…… 1
8 + 1 = 9(环)
【选自教材P70 练习十三 第1题】
二、这节课有什么新探索？
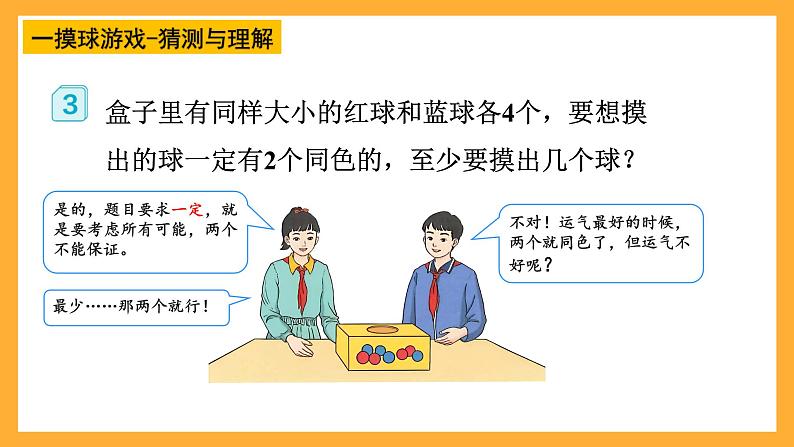
不对！运气最好的时候，两个就同色了，但运气不好呢？
是的，题目要求一定，就是要考虑所有可能，两个不能保证。
盒子里有同样大小的红球和蓝球各4个，要想摸出的球一定有2个同色的，至少要摸出几个球？
一摸球游戏-猜测与理解
想摸什么就能摸到什么吗？
可以只考虑运气最好的情况吗？
应该是刚刚能保证两个同色的个数，不能太多，也不能太少。
8个别说两个球，4个球都能同色啦！题目要求至少。
有道理，比2个多，比8个少。
只摸2个球不能保证同色
我赞成！从小往大试……
活动：摸出三个球，可能有哪些结果？用自己喜欢的方式梳理并整理出来。 所有情况都有两球同色吗？做出你的判断。
摸三个球，一定有两个同色。
还要往后试吗？4个？5个？
是的，摸3个都已经符合了，摸更多，更会符合！
要想摸出的球一定有2个同色的，至少要摸出3个球。
各不同色，最多能摸几个球？
假设每次摸的球都不同色，最多可以摸两个。第三个球无论是什么颜色，都会和前面的球重复……
把红、黄、蓝、白4种颜色的球各10个放到一个袋子里。至少取多少个球，可以保证取到两个颜色相同的球？
假设每次取的球都不同色，最多可以取四个。第五个球无论是什么颜色，都会和前面的球重复……
至少取5个球，可以保证取到两个颜色相同的球。
【选自教材P69 做一做 第2题】
把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少5个球，可以保证取到两个颜色相同的球。
盒子里有同样大小的红球和蓝球各4个，要想摸出的球一定有2个同色的，至少要摸出3个球。
盒子里有 种颜色的球若干个，至少摸 次可以保证取到两个颜色相同的球。
2.和鸽巢问题有什么联系？
3.有什么需要提醒大家注意的？
至少要摸颜色数+1个球。
发现规律至少要摸颜色数+1个球。
反向思考假设法、找最少的情况
六年级至少有2个人在同一天过生日，六（2）班至少有4个人在同一个月过生日。
向东小学六年级共有367名学生，其中六（2）班有37名学生。
假设每个人的生日都不同，闰年有366天，但一共有367名学生，所以至少有两人的生日是同一天。
假设每个人的出生月份都不同，一年有12个月，37 ÷12最多商3，所以至少有4人是同一个月生的。
【选自教材P69 做一做 第1题】
三.鸽巢问题-回顾与反思
1. 给1个正方体木块的6个面分别涂上蓝、黄两种颜色，不论怎么涂至少有3个面涂的颜色相同。为什么？
2. 任意给出3个不同的自然数，其中一定有2个数的和是偶数，请说明理由。
3.把红、蓝、黄3种颜色的筷子各3根混在一起。如果让你闭上眼睛，从中最少拿出几根才能保证一定有2根同色的筷子？
最少拿4根才能保证一定有2根同色的筷子。
3.把红、蓝、黄3种颜色的筷子各3根混在一起。如果让你闭上眼睛，从中最少拿出几根才能保证一定有2根同色的筷子？如果要保证有2双不同色的筷子（指一双筷子为其中一种颜色，另一双筷子为另一种颜色）呢？
如果要保证有两双筷子，最少要拿6根筷子。
完成本课时的相关习题。