数学九年级上册第22章 相似形22.2 相似三角形的判定教学课件ppt

这是一份数学九年级上册第22章 相似形22.2 相似三角形的判定教学课件ppt，共12页。

1.已知一个直角三角形的一条直角边和斜边的长度分别为 1、4,另一个直角三角形的一条直角边和斜边的长度分别为 3、12,则这两个直角三角形 (　    )A.一定相似　　　 B.一定不相似　    C.不一定相似　　　D.无法判断是否相似
解析　因为 = ,所以两个直角三角形的斜边与一条直角边对应成比例,所以这两个直角三角形相似.
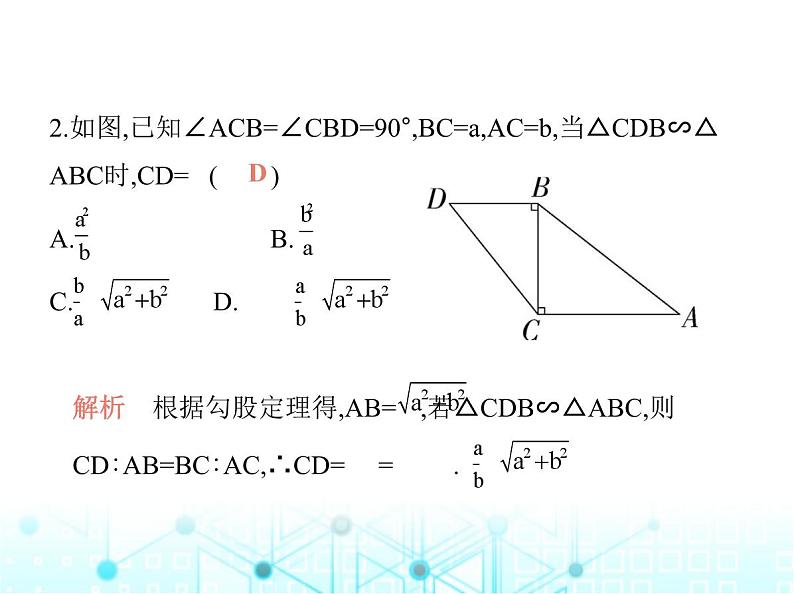
2.如图,已知∠ACB=∠CBD=90°,BC=a,AC=b,当△CDB∽△ ABC时,CD= (　    )A. 　　　 B. C.   　　　D.    
解析　根据勾股定理得,AB= ,若△CDB∽△ABC,则CD∶AB=BC∶AC,∴CD= =   .
3.如图,在矩形ABCD中,AB=2,BC=1,P在DC边上,当AP=　     　    时,△ADP∽△ABC.  
解析　∵在矩形ABCD中,AB=2,BC=1,∴AD=BC=1,AC=  = = .由△ADP∽△ABC得 = ,即 = ,解得AP= .
4.(教材变式·P84T3)根据下列条件判断Rt△ABC和Rt△A'B'C'是否相似,并说明理由,其中∠C=∠C'=90°.(1)AB=14 cm,BC=6 cm,A'B'=7 cm,B'C'=3 cm;(2)AB=  cm,AC=  cm,A'B'=  cm,A'C'=  cm.
解析    (1)Rt△ABC∽Rt△A'B'C'.理由如下:∵ = =2, = =2,∴ = .又∵∠C=∠C'=90°,∴Rt△ABC∽Rt△A'B'C'.(2)Rt△ABC∽Rt△A'B'C'.理由如下:∵ = = , = = ,∴ = .又∵∠C=∠C'=90°,∴Rt△ABC∽Rt△A'B'C'.
5.(教材变式·P83例4)如图,已知∠ACB=∠ABD=90°,AB=8, BC=4,当AD的长为多少时,图中的两个直角三角形相似?(M9 122005) 
解析　∵∠ACB=∠ABD=90°,AB=8,BC=4,∴AC=4 .要使这两个直角三角形相似,有两种情况:当 = 时,Rt△ADB∽Rt△ABC,∴AD= ×8= ;当 = 时,Rt△ABD∽Rt△BCA,∴AD= ×8=16.
∴当AD的长为 或16时,这两个直角三角形相似
解析　由∠C=∠AED=90°,∠CAB=∠D,可知△ACB∽△ DEA,A选项不符合题意;由AD∥BC,可得∠B=∠DAE,又∠C =∠AED=90°,∴△ACB∽△DEA,B选项不符合题意;∵ = 可化为 = ,又∠C=∠AED=90°,∴Rt△ACB∽Rt△DEA,C选项不符合题意;由 = 无法判定两个三角形相似,故选D.
7.(分类讨论思想)(2024安徽阜阳界首期中,14, )如图,在△ABC中,∠C=90°,AC=8,BC=6,D为AB上一点,且AD=2,若 在AC边上取一点E,使△ADE与△ABC相似,则AE的长为     　　　　    .(M9122005)