

九年级上册第22章 相似形22.2 相似三角形的判定优秀课件ppt
展开1. 理解三角形相似的判定定理;(重点)2. 三角形相似的判定定理及应用.(难点)
对应角相等,对应边的比相等的两个多边形为相似多边形.
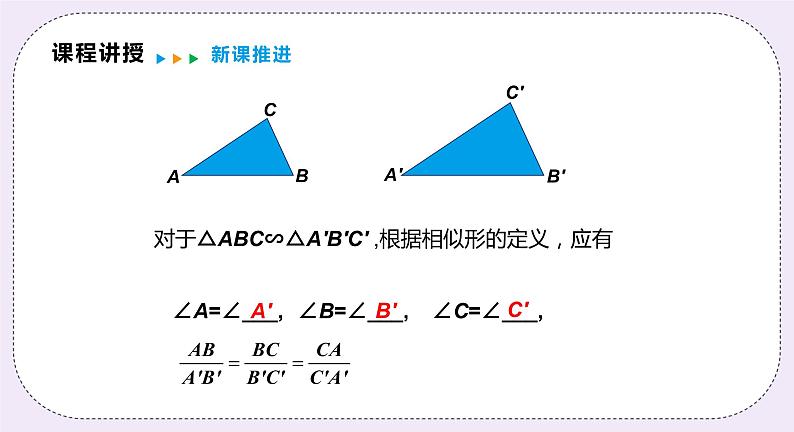
探索1:相似三角形的性质及有关概念
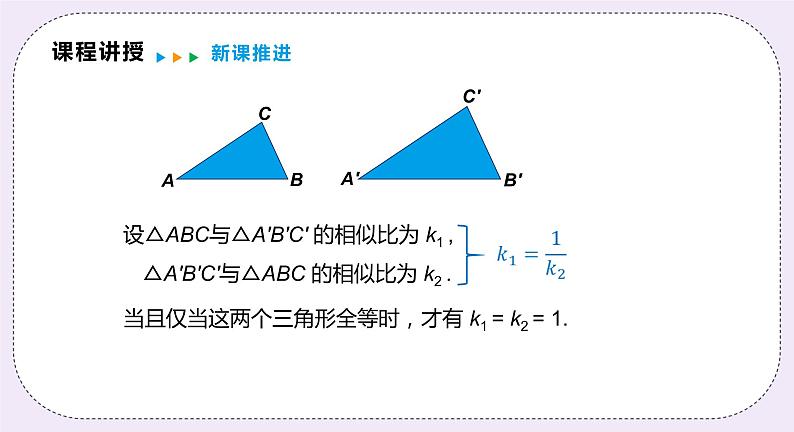
如图,△ABC 与△A′B′C′ 相似, 记作“△ABC∽△A′B′C′”, 读作“△ABC 相似于△A′B′C′”.
对于△ABC∽△A′B′C′ ,根据相似形的定义,应有
设△ABC与△A′B′C′ 的相似比为 k1 ,
△A′B′C′与△ABC 的相似比为 k2 .
当且仅当这两个三角形全等时,才有 k1 = k2 = 1.
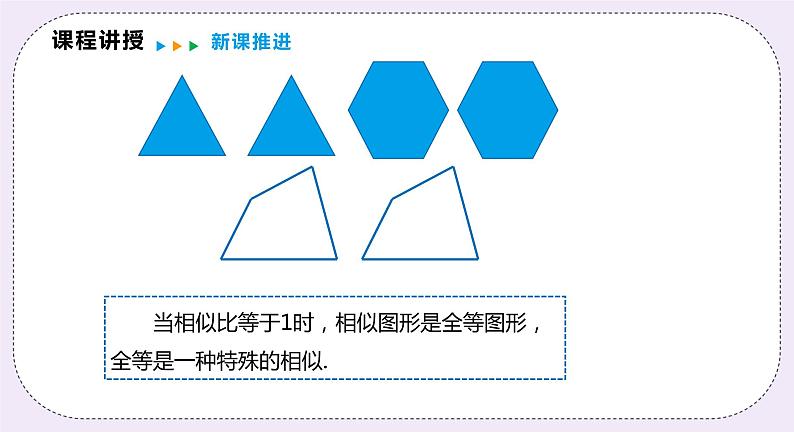
当相似比等于1时,相似图形是全等图形,全等是一种特殊的相似.
1.两个全等三角形一定相似吗?为什么?
2.两个直角三角形一定相似吗?为什么?两个等腰直角三角形呢?
3.两个等腰三角形一定相似吗?为什么?两个等边三角形呢?
△ABC与△DEF的各角度数和边长如图所示,则△ABC与△DEF能否相似?说明理由.
解:因为∠A=70°,∠B=60°,所以∠C=50°. 因为∠F=60°,∠E=50°,所以∠D=70°. 所以∠A=∠D,∠B=∠F,∠C=∠E.
∴ △ABC∽△DFE.
如图,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=58cm,∠BAC=45°,∠ACB=40°,求:(1)∠AED和∠ADE的度数;(2)DE的长.
解:(1)∵△ABC∽△ADE, ∴∠AED=∠ACB=40°.在△ADE中,∠ADE=180°-40°-45°=95°;
(2) ∵△ABC∽△ADE.
∴DE=36.25(cm).
探索2:平行线与相似三角形
如图, 在△ABC 中, D 为AB上任意一点, 过点 D 作 BC 的平行线 DE, 交 AC 于点 E. 那么, △ADE 与△ABC 相似吗?
过点 D 作 AC 的平行线交 BC 于点 F.
∵ DE // BC, DF // AC ,
∵ 四边形DFCE是平行四边形,
∴DE = FC, 即
∵ (对应边成比例)
又∵∠A=∠A, ∠B=∠ADE, ∠C=∠AED,(对应角相等)
在△ADE 和△ABC 中,
∴△ADE ∽△ABC .
当 DE 在 AB, AC 的延长线或 BA, CA 的延长线上时,△ADE与△ABC 相似吗?
如果再作 MN∥DE ,共有多少对相似三角形?
如图,已知在平行四边形ABCD中,E为AB延长线上一点,AB=3BE,DE与BC相交于点F.请找出图中各对相似三角形,并求出相应的相似比.
解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴△BEF∽△CDF,△BEF∽△AED,∴△CDF∽△AED.故当△BEF∽△CDF时,相似比为BE: CD=BE: AB=1:3;当△BEF∽△AED时,相似比为BE: AE=1:4;当△CDF∽△AED时,相似比为CD: AE=3:4.
已知:如图是一束光线射入室内的平面图,上檐边缘射入的光线照在距窗户2.5m处,已知窗户AB高为2m,B点距地面高为1.2m,求下檐光线的落地点N与窗户的距离NC.
解:∵AM∥BN, ∴△NBC∽△MAC,
1.如果两个三角形的相似比为1,那么这两个三角形_____.2.若△ABC与△A′B′C′相似,一组对应边的长为AB=3 cm,A′B′= 4 cm,那么△A′B′C′与△ABC的相似比是____ .3.若△ABC的三条边长分别为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12 cm,那么△ A′B′C′的最大边长是_____.
4.已知△ABC的三条边长3cm,4cm,5cm,△ABC∽△A1B1C1,那么△A1B1C1的形状是__________,又知△A1B1C1的最大边长为25cm,那么△A1B1C1的面积为________.
5.若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠ C′的度数是( ) A.55° B.100° C.25° D.不能确定
如图, 点 D 在△ABC 的边 AB 上, DE//BC, DE交 AC 于点E, DF//AC, DF 交 BC 于点F, 判断下列比例式子是否成立.
如图, △ABC 中, DE//BC, GF//AB, DE、GF 交于点O, 则图中与△ABC 相似的三角形共有多少个?请你写出来.
解:与△ABC 相似的三角形有3个,△ADE、△GFC、△GOE.
如图,在△ABC中,DG//EH//FI//BC,(1)请找出图中所有的相似三角形;(2)如果 AD = 1, DB = 3, 那么DG∶BC=______.
△ADG、△AEH、△AFI、△ABC.
沪科版九年级上册22.3 相似三角形的性质一等奖课件ppt: 这是一份沪科版九年级上册22.3 相似三角形的性质一等奖课件ppt,共25页。PPT课件主要包含了学习目标及重难点,课程导入,相似比,课程讲授,又∠D=∠A,随堂小练习,习题解析,习题1,习题2,又∵∠D∠A等内容,欢迎下载使用。
沪科版九年级上册22.3 相似三角形的性质一等奖课件ppt: 这是一份沪科版九年级上册22.3 相似三角形的性质一等奖课件ppt,共28页。PPT课件主要包含了学习目标及重难点,课程导入,量一量猜一猜,课程讲授,变式一,∠C∠C′,课堂练习,习题1,习题2等内容,欢迎下载使用。
初中数学沪科版九年级上册22.1 比例线段优质课件ppt: 这是一份初中数学沪科版九年级上册22.1 比例线段优质课件ppt,共25页。PPT课件主要包含了学习目标及重难点,课程导入,由此得到如下结论,平行线等分线段定理,几何语言,且ABBC,两条直线被,对应线段是指,可简记为,所得的对应线段等内容,欢迎下载使用。













