初中数学沪科版九年级上册22.2 相似三角形的判定精品课件ppt

这是一份初中数学沪科版九年级上册22.2 相似三角形的判定精品课件ppt，共17页。PPT课件主要包含了学习目标及重难点，课程导入，课程讲授，课堂练习，习题1，习题2，习题3等内容，欢迎下载使用。

1.掌握直角三角形相似的判定；（重点）2.能熟练地运用直角三角形相似的判定定理.（难点）
观察两副三角尺如图，其中同样角度（30°与60°，或45°与45°）的两个三角尺大小可能不同，但它们看起来是相似的．一般地，如果两个三角形有两组对应角相等，它们一定相似吗？对于直角三角形，类似于判定三角形全等的HL方法，我们能不能通过两边来判断两个三角形相似呢？
探索1：利用边判定直角三角形相似
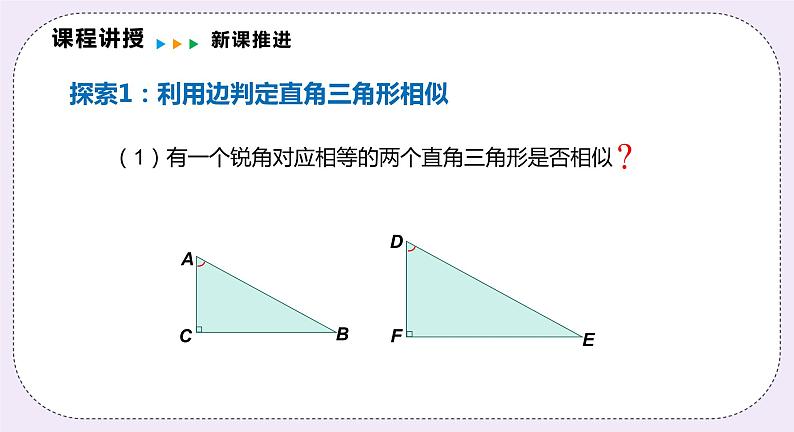
（1）有一个锐角对应相等的两个直角三角形是否相似
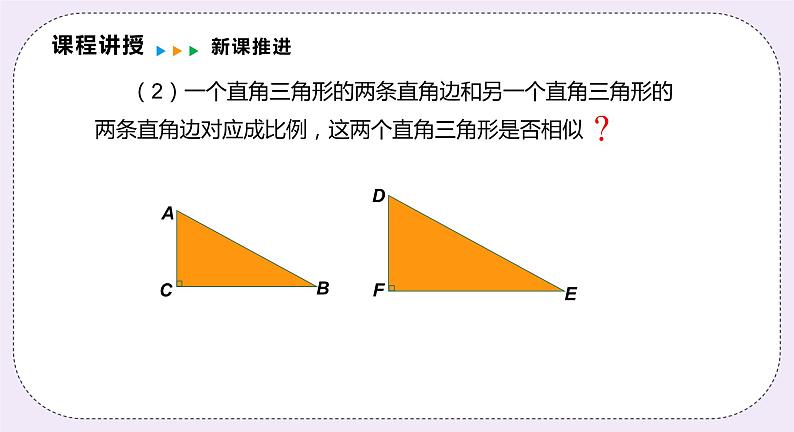
（2）一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例，这两个直角三角形是否相似
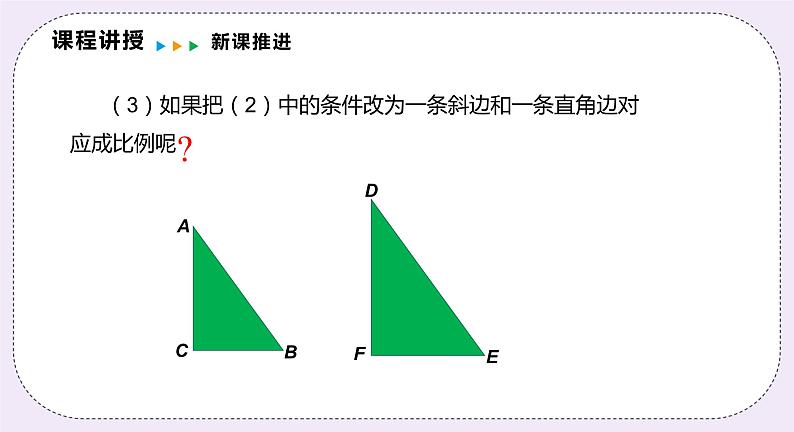
（3）如果把（2）中的条件改为一条斜边和一条直角边对应成比例呢
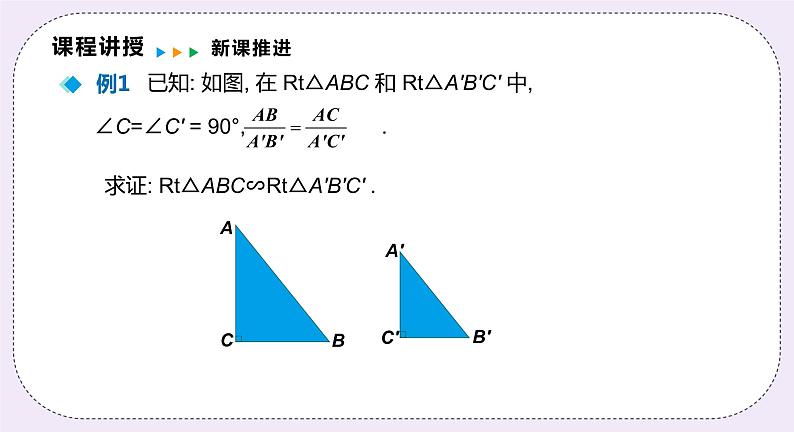
已知: 如图, 在 Rt△ABC 和 Rt△A′B′C′ 中, ∠C=∠C′ = 90°, .
求证: Rt△ABC∽Rt△A′B′C′ .
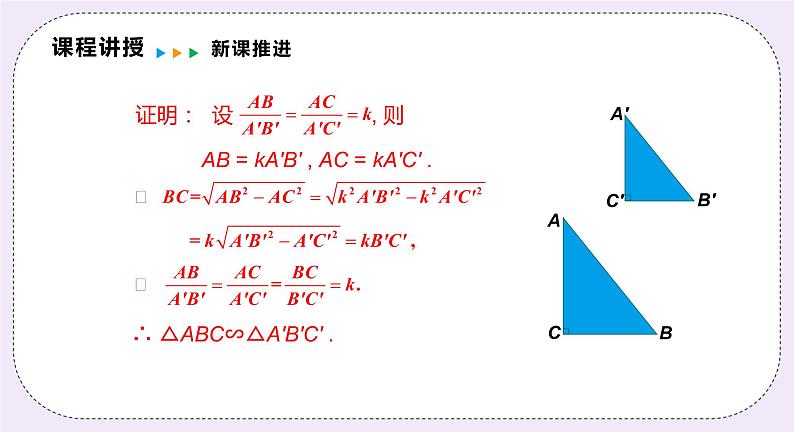
证明： 设 , 则
AB = kA′B′ , AC = kA′C′ .
∴ △ABC∽△A′B′C′ .
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例， 那么这两个直角三角形相似.
那么△ABC∽△A1B1C1.
Rt△ABC 和 Rt△A1B1C1.
如图, ∠ABC =∠CDB = 90°, CB = a, AC = b. 问当 BD 与 a, b 之间满足怎样的函数表达式时, 以点 A, B, C 为顶点的三角形与以点 C, D , B 为顶点的三角形相似？
解 ∵ ∠ABC=∠CDB=90°,
当 时, △ABC∽△CDB.
又当 时, △ABC∽△BDC.
答: 当 或 时, 以点 A, B, C 为顶点的三角形与以点 C, D, B 为顶点的三角形相似.
锐角三角形ABC 的边 AB, AC 上的高 CE, BF相交于点 D, 请写出图中的两对相似三角形.
△BED ∽△CFD.
△BED ∽△BFA.
在 Rt△ABC 与△A′B′C′中,∠C =∠C′ = 90°, 当具有下列条件时, 这两个直角三角形是否相似, 为什么？
（1）AB=10cm, AC=8cm, A′B′=15cm, B′C′=9cm;（2）AB=5cm, AC=4cm, A′C′=12cm, B′C′=9cm.
(1) 解: 由勾股定理得 A′C′=12 cm,
∴ △ABC ∽△A′B′C′.
（2）AB=5cm, AC=4cm, A′C′=12cm, B′C′=9cm.
解: 由勾股定理得 A′B′=15 cm,
∴△ABC ∽△A′B′C′.
如图，已知Rt△ABC和Rt△A′B′C′中∠A=∠A′=90°，AD，A′D′分别是两个三角形斜边上的高，且CD∶C′D′=AC∶A′C′请说明：△ABC∽△A′B′C′．