资料中包含下列文件,点击文件名可预览资料内容












还剩19页未读,
继续阅读
所属成套资源:新人教a版数学必修第一册PPT课件+分层作业(含解析)
成套系列资料,整套一键下载
4.3.1 对数的概念PPT+分层作业+答案解析
展开
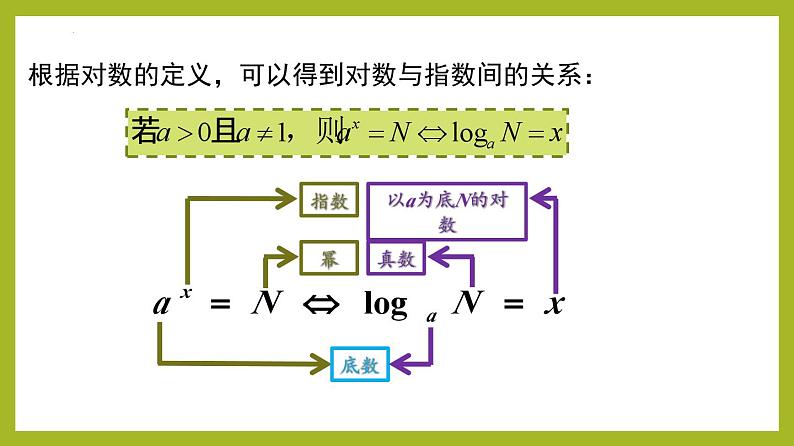
人教A版2019必修第一册第 4章 指数函数与对数函数4.3.1 对数的概念目 录1 学习目标2 新课讲解3 课本例题4 课本练习5 题型分类讲解6 随堂检测7 课后作业学习目标1.理解对数的概念,掌握对数的性质,能进行简单的对数计算.(重点、难点)2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化.(重点)3.理解常用对数、自然对数的概念及记法. 情境导入 对数的概念,首先是由苏格兰数学家John Napier(纳皮尔,1550~1617)提出的.那时候天文学是热门学科.可是由于数学的局限性,天文学家不得不花费很大精力去计算那些繁杂的“天文数字”,浪费了若干年甚至毕生的宝贵时间.Napier也是一位天文爱好者,他感到,“没有什么会比数学的演算更加令人烦恼……诸如一些大数的乘、除、平方、立方、开方……因此我开始考虑……怎样才能排除这些障碍.”经过20年潜心研究大数的计算技术,他终于独立发明了对数,并于1614年出版的名著《奇妙的对数定律说明书》(“Mirifici logarithmorum canonis descriptio”)中阐明了对数原理,后人称为纳皮尔对数(NaplogX).【思考1】(1)那么1个这样的细胞分裂x次得到细胞个数N是多少?分裂多少次得到细胞个数为16个,256个呢? (2)如果已知细胞分裂后的个数N,如何求分裂次数呢?【提示】 (1)N=2x,4次,8次. (2)由2x=N 可知当N 已知时,x 的值即为分裂次数.特别注意::logaN是一个数,是一种取对数的运算,结果仍是一个数,不可分开书写. 通常,将以10为底的对数叫做常用对数,并把log10N记为lgN;另外,在科技、经济以及社会生活中经常使用以无理数e=2.71828…为底数的对数称为自然对数,并把logeN简记为lnN . 一般地,如果ax=N,(a>0且a≠1),则数x叫做以a为底N的对数记作x=logaN,其中a叫底数,N叫真数.根据对数的定义,可以得到对数与指数间的关系:例题1 将下列指数式写成对数式例题2 将下列对数式写成指数式指数式、对数式的互化技巧:“底数不变,左右交换”1.指数式与对数式的转化根据对数的定义,可以得到对数与指数间的关系:由指数和对数的这个关系,可以得到关于对数的如下结论:(真数一定为正数)利用对数与指数间的关系证明这两个结论. 因为ax=N,(a>0且a≠1),由指数函数的性质可知:N>0,所以负数和0没有对数. (真数N一定为正数)例3 求下列各式中的x 的值:2.对数式求对数、真数、底数1.把下列指数式化为对数式,对数式化为指数式。(1)23=8; (2) ; (3) ;课本练习 1.把下列指数式化为对数式,对数式化为指数式。(4)log39=2; (5)lg n=2.3; (6) .答案: 2.求下列各式中的值。3.求下列式中 的值 . 题型一:对数的概念 题型分类讲解 题型二:利用指数式与对数式的互化求变量 题型三:对数的性质及对数恒等式 随堂检测对数的性质对数式与指数式的互化课堂小结
相关资料
更多










