初中数学北师大版七年级下册2 探索直线平行的条件教学课件ppt

这是一份初中数学北师大版七年级下册2 探索直线平行的条件教学课件ppt，共25页。PPT课件主要包含了学习目标，导入新课，新知探究，典例精析，当堂练习，课堂小结等内容，欢迎下载使用。

1.理解并掌握内错角、同旁内角的概念，能够区分同位角、内错角和同旁内角并确定其个数；2.理解利用内错角相等、同旁内角互补来判定两直线平行的探究过程；（重点）3.会利用三种判定方法证明两直线平行，并能够运用其解决实际问题.（难点）
4.平行于同一条直线的两条直线　　　　. 
2.两条直线被第三条直线所截,如果同位角　　　　,那么这两条直线平行.简称为　　　　 　　　　　　　. 
1.如图所示，具有∠1和∠2这样位置关系的角称为　　 　　. 
同位角相等,两直线平行
3.过直线外一点　　 　　 一条直线与这条直线平行. 
小明身边只有一个量角器，他通过测量某些角的大小就能知道这个画板的上、下边缘是否平行，你知道他是怎样做的吗？
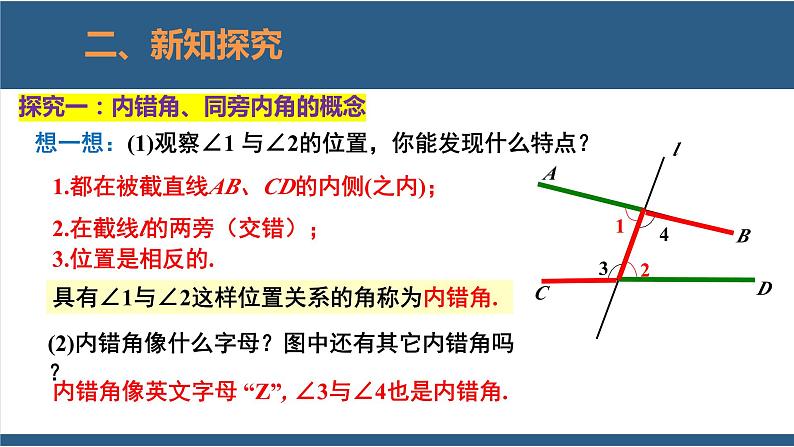
探究一：内错角、同旁内角的概念
想一想：(1)观察∠1 与∠2的位置，你能发现什么特点？
1.都在被截直线AB、CD的内侧(之内)；
2.在截线l的两旁（交错）；3.位置是相反的.
具有∠1与∠2这样位置关系的角称为内错角.
内错角像英文字母 “Z”,
(2)内错角像什么字母？图中还有其它内错角吗？
∠3与∠4也是内错角.
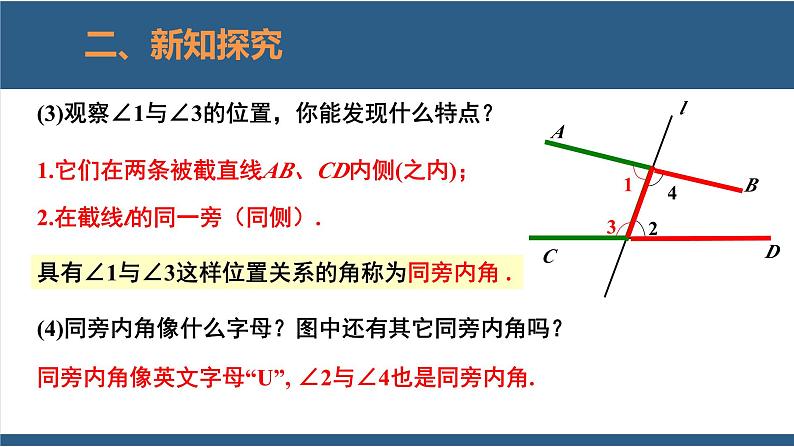
(3)观察∠1与∠3的位置，你能发现什么特点？
1.它们在两条被截直线AB、CD内侧(之内)；
2.在截线l的同一旁（同侧）.
具有∠1与∠3这样位置关系的角称为同旁内角 .
(4)同旁内角像什么字母？图中还有其它同旁内角吗？
同旁内角像英文字母“U”,
∠2与∠4也是同旁内角.
探究二：利用内错角、同旁内角判定两直线平行
议一议：(1)内错角满足什么关系时，两直线平行？ 为什么？
内错角相等时，两直线平行.
证明： ∵ 1=3(对顶角相等）， 1=2（已知），  2=3.  a//b(同位角相等，两直线平行）.
直线平行的判定方法2：两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简称为：内错角相等，两直线平行.
应用格式（几何语言）：
证明: ∵1+2=180°（已知） 1+3=180°（邻补角定义） 2=3（同角的补角相等） a//b（同位角相等，两直线平行）
议一议：(2)同旁内角满足什么关系时，两直线平行？ 为什么？
同旁内角相加等于180°时，两直线平行.
直线平行的判定方法3：两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简称为：同旁内角互补，两直线平行.
内错角相等，两直线平行
同旁内角互补,两直线平行
再找一组平行线，并说明你的理由．
∵∠BCA=∠EAC∴BC∥AE（内错角相等，两直线平行）．
∵∠BCA=∠CDE∴AC∥DE（同位角相等，两直线平行）．
判定两条直线平行的方法:(1)定义法;(2)同位角相等,两直线平行;★(3)内错角相等,两直线平行;★(4)同旁内角互补,两直线平行;★(5)平行于同一条直线的两条直线平行.★
解:(1)由∠ABD=∠CDB,可以得出AB∥CD.理由:内错角相等,两直线平行.(2)由∠CBA+∠BAD=180°,可以得出AD∥BC.理由:同旁内角互补,两直线平行.(3)由∠ABC=∠DCE,可以得出AB∥CD.理由:同位角相等,两直线平行.
解:BE∥CF.理由:因为AB⊥BC,BC⊥CD,所以∠ABC=∠DCB=90°.又因为∠1=∠2,所以∠ABC-∠1=∠DCB-∠2,即∠CBE=∠BCF,所以BE∥CF（内错角相等,两直线平行）.
内错角相等,两直线平行
平行于同一条直线的两条直线平行
解:AB∥CD,BC∥DE.理由:因为∠1=47°,所以∠ABC=∠1=47°.又因为∠2=133°,所以∠ABC+∠2=180°,所以AB∥CD.因为∠2=133°,所以∠BCD=180°-∠2=47°.又因为∠D=47°,所以∠BCD=∠D,所以BC∥DE.
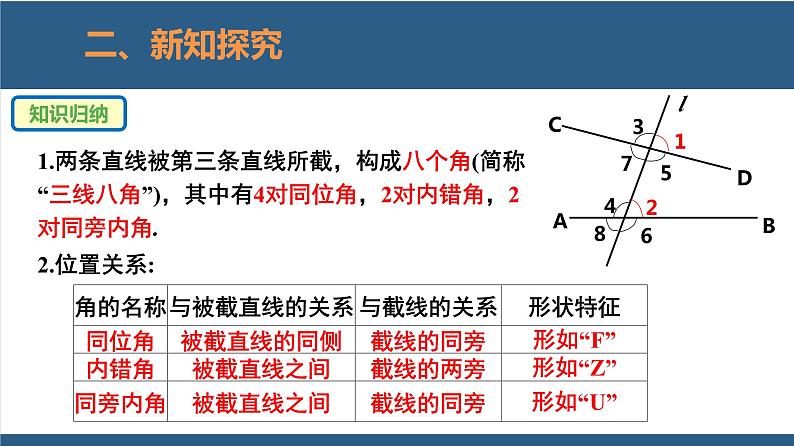
2.判定两条直线平行的方法