初中数学北师大版七年级下册第二章 相交线与平行线3 平行线的性质教学ppt课件

这是一份初中数学北师大版七年级下册第二章 相交线与平行线3 平行线的性质教学ppt课件，共23页。PPT课件主要包含了学习目标，导入新课，复习回顾，平行线的判定，同位角，内错角，同旁内角，∠1∠2，∠3∠2，∠2+∠4180°等内容，欢迎下载使用。

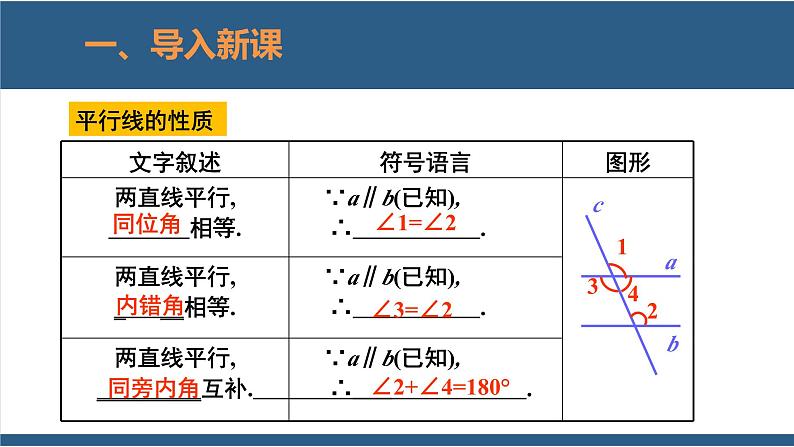
1.进一步掌握平行线的性质，运用两条直线是平行判断角的数量关系；（重点）2.能够根据平行线的性质与判定进行简单的推理与计算.（难点）
探究：平行线性质与判定的综合运用
(1)∠1与∠2是内错角,若∠1=∠2,则根据“内错角相等,两直线平行”,可得BF∥CE.
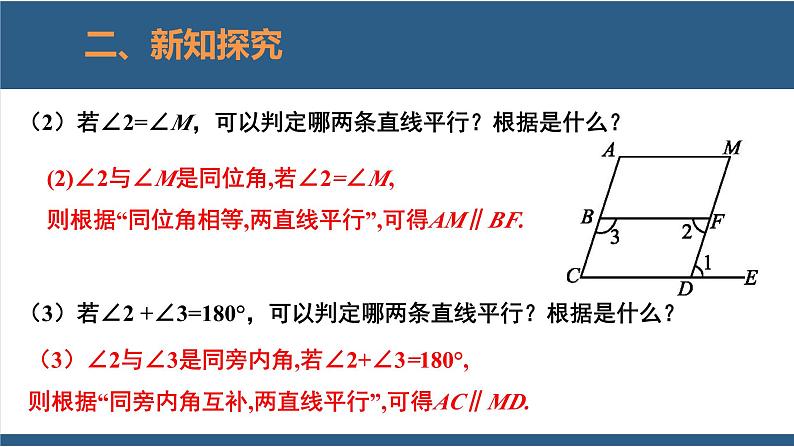
（3）∠2与∠3是同旁内角,若∠2+∠3=180°,则根据“同旁内角互补,两直线平行”,可得AC∥MD.
（3）若∠2 +∠3=180°，可以判定哪两条直线平行？根据是什么？
（2）若∠2=∠M，可以判定哪两条直线平行？根据是什么？
(2)∠2与∠M是同位角,若∠2=∠M,则根据“同位角相等,两直线平行”,可得AM∥BF.
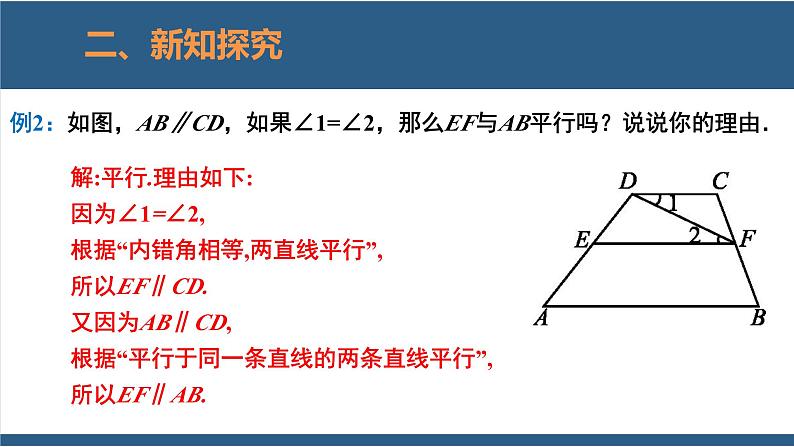
解:平行.理由如下:因为∠1=∠2,根据“内错角相等,两直线平行”,所以EF∥CD.又因为AB∥CD,根据“平行于同一条直线的两条直线平行”,所以EF∥AB.
解:因为∠A=∠F,所以DF∥AC（内错角相等，两直线平行）,所以∠D=∠ABD（两直线平行，内错角相等）.因为∠C=∠D,所以∠ABD=∠C（等量代换）,所以BD∥CE（同位角相等，两直线平行）.
解:因为a∥b,根据“两直线平行,内错角相等”,所以∠2=∠1=107°.因为c∥d,根据“两直线平行,同旁内角互补”,所以∠1+∠3=180°,所以∠3=180°-∠1=180°-107°=73°.
解：∵AE∥CD∴∠2=∠1=37°（两直线平行，内错角相等）∴∠BAE=∠D=54°（两直线平行，同位角相等）
想一想：两条直线被第三条直线所截，如果同位角相等，那么内错角相等吗？同旁内角互补吗？
两条直线被第三条直线所截，如果同位角相等
内错角相等，同旁内角互补.
思考：平行线三个性质的条件是什么？结论是什么？它与判定有什么区别？
解:∵AD∥BC,∴∠A=∠GBC(两直线平行，同位角相等).∵∠D+∠GBC=180°,∴∠A+∠D=180°,∴DC∥AB(同旁内角互补，两直线平行).∵EF∥DC,∴AB∥EF(平行于同一条直线的两条直线平行).
解析：由∠1=∠2，可根据“同位角相等，两直线平行”判断出a∥b，可得∠3=∠5.再根据邻补角互补，可以计算出∠4的度数．∵∠1=∠2,∴a∥b，∴∠3=∠5.∵∠3=70°，∴∠5=70°,∴∠4=180°－70°=110°.
1.有下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.其中是平行线的性质的是(　　)A.①B. ②③C.④D. ①④
内错角相等,两直线平行
两直线平行,同位角相等
解:∵EF∥AD,∴∠1=∠BAD(两直线平行，同位角相等).又∵∠1=∠2,∴∠2=∠BAD(等量代换),∴AB∥DG(内错角相等，两直线平行),∴∠BAC+∠AGD=180°(两直线平行，同旁内角互补).∵∠BAC=70°,∴∠AGD=110°.
解:∵∠1=∠2(已知),∴CD∥AB(同位角相等,两直线平行),∴∠ADC+∠A=180°(两直线平行,同旁内角互补).又∵∠A=∠C(已知),∴∠ADC+∠C=180°(等量代换),∴AE∥BC(同旁内角互补,两直线平行).
解:(1)BF∥DE.理由如下:因为∠AGF=∠ABC,所以GF∥BC,所以∠1=∠FBC.因为∠1+∠2=180°,所以∠FBC+∠2=180°,所以BF∥DE.(2)因为BF∥DE,DE⊥AC,所以∠AFB=∠AED=90°.因为∠1+∠2=180°,∠2=140°,所以∠1=40°,所以∠AFG=90°-40°=50°.
谈谈本节课你有哪些收获？