初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数复习课件ppt

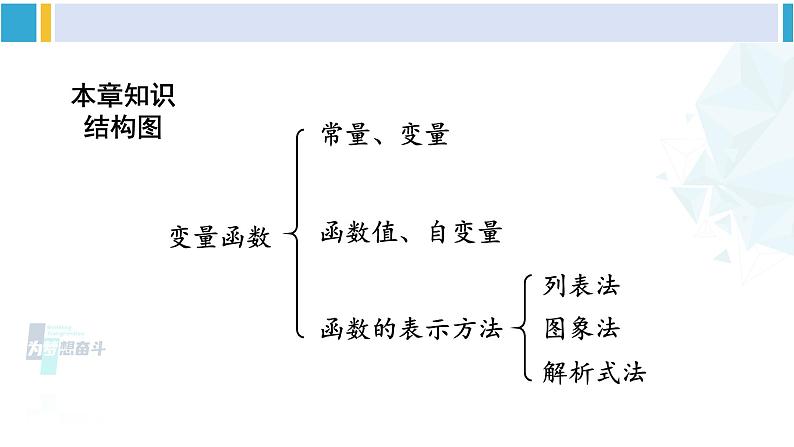
这是一份初中数学人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数复习课件ppt，共39页。PPT课件主要包含了本章知识结构图，变量函数，自变量，函数的表示方法，列表法，图象法，解析式法，ykx，图象的平移，实际应用等内容，欢迎下载使用。
y = kx（ k 是常数，k ≠ 0 ）
当 k > 0 时，直线 y = kx 经过一、三象限
当 k < 0 时，直线 y = kx 经过二、四象限
当 k > 0 时， y 随 x 的增大而增大
当 k < 0 时， y 随 x 的增大而减小
y = kx + b（ k，b 是常数，k ≠ 0 ）
当 k > 0，b > 0 时，直线 y = kx 经过一、二、三象限
当 k > 0，b < 0 时，直线 y = kx 经过一、三、四象限
当 k < 0，b > 0 时，直线 y = kx 经过一、二、四象限
当 k < 0，b < 0 时，直线 y = kx 经过二、三、四象限
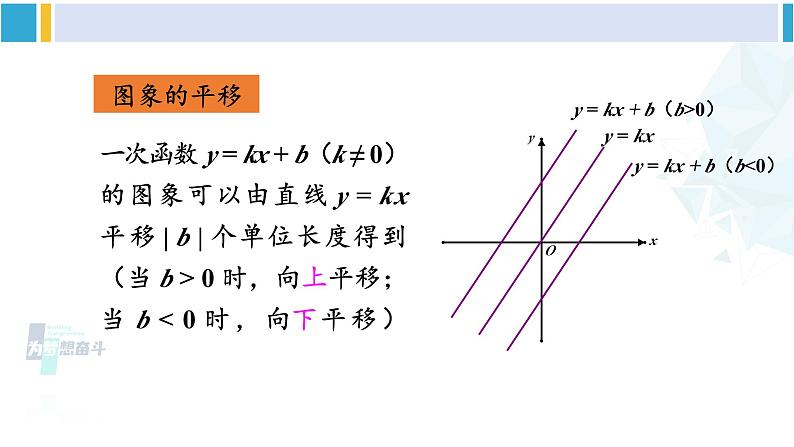
一次函数 y = kx + b（k ≠ 0）的图象可以由直线 y = kx 平移 | b | 个单位长度得到（当 b > 0 时，向上平移；当 b < 0 时，向下平移）
y = kx + b（b>0）
y = kx + b（b 0； （2）y < 0.
解:在平面直角坐标系中画出函数 y = 3x -15 的图象:（1）由图象知，当 x > 5 时，直线在 x 轴的上方，即此时 y > 0，所以当 x > 5 时，y > 0；
【选自教材P107 第5题】
（2）由图象知，当 x < 5 时，直线在 x 轴的下方，即此时 y < 0，所以当 x < 5 时，y < 0.
6. 在某火车站托运物品时，不超过 1 kg 的物品需付 2 元，以后每增加 1 kg（不足 l kg 按 1 kg 计）需增加托运费0.5元. 设托运 p kg（p 为整数）物品的费用为 c 元. 试写出 c 的计算公式.
【选自教材P107 第6题】
7. 某水果批发市场规定，批发苹果不少于 100 kg 时，批发价为 2.5元/kg. 小王携带现金 3 000 元到这市场采购苹果，并以批发价买进．设购买的苹果为 x kg，小王付款后还剩余现金 y 元. 试写出 y 关于 x 的函数解析式，并指出自变量 x的取值范围.
求自变量的取值范围1. 批发苹果不少于 100 kg ，2. y ≥ 0.
【选自教材P107 第7题】
解: y 与 x 之间的函数解析式为 y = 3 000 - 2.5x ，因为剩余现金 y ≥ 0，所以 3 000-2.5x ≥ 0，所以 x ≤ 1 200，所以自变量 x 的取值范围是 100 ≤ x ≤ 1 200.
8. 匀速地向一个容器内注水，最后把容器注满．在注水过程中，水面高度 h 随时间 t 的变化规律如图所示（图中 OABC 为一折线）. 这个容器的形状是下图中哪一个？匀速地向另两个容器注水时，你能画出水面高度 h 随时间 t 变化的图象（草图）吗？
【选自教材P108 第8题】
解:从图象上看，在注水过程中，容器的中间部分的水面高度 h 随时间 t 的变化最缓慢，其次是容器的下面部分，变化最迅速的应该是容器的上面部分，因此可以断定这个容器的形状是图（3）.（1）向图（1）的容器注水时水面高度 h 随时间 t 变化的图象:
（2）向图（2）的容器注水时水面高度 h 随时间 t 变化的图象:
9. 已知等腰三角形周长为 20.（1）写出底边长 y 关于腰长 x 的函数解析式（x 为自变量）；（2）写出自变量取值范围；（3）在直角坐标系中，画出函数图象.
解:（1）因为2x + y = 20，所以 y = 20 - 2x. 所以底边长 y 与腰长 x 之间的函数关系式为 y = 20 - 2x.
【选自教材P108 第9题】
（2）因为三角形任意两边之和要大于第三边，
解得 5 < x < 10，即自变量 x 的取值范围是 5 < x < 10.
10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （1）求 S 关于 x 的函数解析式； （2）求 x 的取值范围； （3）当 S = 12 时，求 P 点坐标； （4）画出函数 S 的图象.
【选自教材P108 第10题】
利用三角形的面积求一次函数的解析式，关键是要找到合适的底和高.
解:（1）因为动点 P(x，y) 在第一象限，所以 x > 0，y > 0.因为 x + y = 10，所以 y = 10 - x ，
所以 ，
即 S 关于 x 的函数解析式为 S = -4x + 40；
10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （1）求 S 关于 x 的函数解析式；
10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （2）求 x 的取值范围； （3）当 S = 12 时，求 P 点坐标；
（2）因为点 P 在第一象限内，所以 x 的取值范围是0 < x < 10；
（3）当 S = 12 时，-4x + 40 = 12，x = 7，则 y = 10-x = 3，所以当 S = 12 时，P 点的坐标为（7，3）.
10. 已知点 A（8，0）及在第一象限的动点 P（x，y），且 x＋y = 10. 设△OPA 的面积为 S. （4）画出函数 S 的图象.
（4）函数 S 的图象如图所示:
11.（1）画出函数 y = | x -1 | 的图象. （2）设 P(x,0) 是 x 轴上的一个动点，它与 x 轴上表示-3 的点的距离为 y. 求 y 关于 x 的函数解析式，并画出 这个函数的图象.
【选自教材P108 第11题】
（2） y = | x - ( -3) | = | x + 3 | = 这个函数的图象如图所示：
x + 3（x ≥ -3），-x -3（x < -3），
12. A，B 两地相距 25 km. 甲 8:00 由 A 地出发骑自行车去 B 地，速度为 10 km/h；乙 9:30 由 A 地出发乘汽车也去 B 地，速度为40 km/h. （1）分别写出两个人的行程关于时刻的函数解析式； （2）乙能否在途中超过甲？如果能超过，何时超过？
【选自教材P108 第12题】
这题是行程问题，由于是以平均速度考虑问题，因此两人的运动形式都按匀速运动考虑.
解:（1）设甲、乙行驶中的时刻为 x 时，甲、乙行驶的路程分别为 y甲，y乙，则有 y甲 = 10(x-8) = 10x-80 (8 ≤ x ≤ 10.5)，y乙= 40(x - 9.5) = 40x - 380 (9.5≤ x ≤ 10.125)；
（2）令 y甲< y乙，则10x-80 < 40x-380. 所以 x > 10，即 10 时以后乙超过甲.
一个有进水管与出水管的容器，从某时刻开始 4 min 内只进水不出水，在随后的 8 min 内既进水又出水，每分的进水量和出水量是两个常数.容器内的水量 y（单位:L）与时间 x（单位:min）之间的关系如图所示. （1）当 0 ≤ x ≤ 4 时，求 y 关于 x 的函数解析式.（2）当 4 < x ≤ 12 时，求 y 关于 x 的函数解析式.（3）每分进水、出水各多少升？
【选自教材P108 第13题】
解:（1）设 y 关于 x 的函数解析式为 y = kx (0 ≤ x ≤ 4).由题意知 20 = 4k，解得 k = 5. 所以当 0 ≤ x ≤ 4 时，y 关于 x 的函数解析式为 y = 5x.
（1）当 0 ≤ x ≤ 4 时，求 y 关于 x 的函数解析式.
（2）当 4 < x ≤ 12 时，求 y 关于 x 的函数解析式.
（2）设 y 关于 x 的函数解析式为 y = k'x + b' ( 4< x ≤ 12 ).
（3）每分进水、出水各多少升？
一次越野赛跑中，当小明跑了 1600 m 时，小刚跑了1 450 m. 此后两人分别以 a m/s 和 b m/s 匀速跑. 又过100 s 时小刚追上小明，200 s 时小刚到达终点，300 s 时小明到达终点．这次越野赛跑的全程为多少米？
解: 根据题意得方程组:
所以 1600 + 300×1.5 = 2050 (m)，即这次越野赛跑的全程为 2050 m.
【选自教材P109 第14题】
A 城有肥料 200 t，B 城有肥料 300 t. 现要把这些肥料全部运往 C，D 两乡.从 A 城往 C，D 两乡运肥料的费用分别为 20 元/t 和 25 元/t；从 B 城往 C，D 两乡运肥料的费用分别为 15 元/t 和 24 元/t. 现 C 乡需要肥料 240 t，D 乡需要肥料 260 t，怎样调运可使总运费最少？
【选自教材P109 第15题】