数学八年级上册4.1 平方根示范课课件ppt

这是一份数学八年级上册4.1 平方根示范课课件ppt，共18页。PPT课件主要包含了课时导入，知识点，平方根的，感悟新知，开平方，平方根的性质，课堂小结，平方根等内容，欢迎下载使用。

想一想(1)9的算术平方根是3,也就是说，3的平方是9. 还有其他的数，它的平方也是9吗？(2)平方等于 的数有几个？平方等于0.64的 数呢？
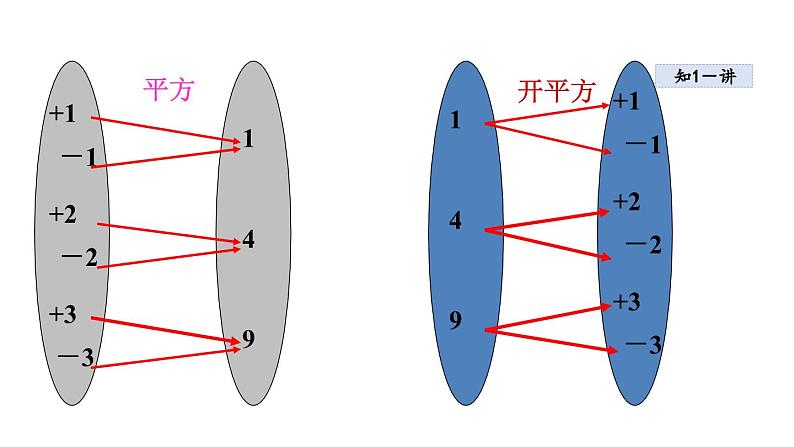
1. 平方根的定义如果x2=a(a ≥ 0)，那么x 叫做a 的平方根，也称为二次方根.2. 表示方法正数a 的两个平方根记作± ，读作正、负根号a. 中正数a 的正的平方根记作 ，正数a 的负的平方根记作－ .
特别解读1. 求一个正数的平方根，先找出平方等于这个正数的数，这样的数有两个，它们互为相反数，因而这两个数均为这个正数的平方根.2. (a ≥ 0)实际上是省略了2 中的2，2 叫做根指数.
3. 开平方(1) 定义 求一个数的平方根的运算叫做开平方.(2) 开平方和加、减、乘、除、乘方一样，指的是一种运算，平方根是开平方运算的结果.
(3) 平方与开平方是互逆运算，平方的结果叫做幂，开平方的结果叫做平方根. 我们可以用平方运算来验证开平方的结果是否正确.
[易错题] 求下列各数的平方根：(1)16； (2)0； (3)0.49； (4) ； (5)－9.
解题秘方：先根据平方运算找出平方等于这个数的数，然后根据平方根的定义确定平方根.
特别提醒 如果一个数为带分数， 一般先将其化为假分数， 再求平方根； 如果有平方运算， 那么先用平方运算求出结果，针对结果再求平方根；如果这个正数a不能写成有理数的平方的形式， 那么可以将a 的平方根表示成± (a ≥ 0).
解:(1)因为(±4)2=16，所以16 的平方根是±4.(2)因为02=0，所以0 的平方根是0.(3)因为(±0.7)2=0.49，所以0.49 的平方根是±0.7.(4)因为 = ，所以 的平方根是± .(5)因为－9 ＜ 0，所以－9 没有平方根.
议一议 (1)一个正数有几个平方根？ (2)0有几个平方根？ (3)负数呢？
1. 一个正数有两个平方根，它们互为相反数；2. 0 的平方根是0；3. 负数没有平方根.
(1)一个正数的平方根是2a－1 和a－5，则这个正数是多少？(2)已知2a－1 与－a+2 是m 的平方根，求m 的值.
解题秘方：根据平方根的性质，找出两个平方根之间的关系列方程求值.
解法提醒1. 正数有两个平方根，它们互为相反数，根据互为相反数的两数和为0，列方程先求出a，再根据平方根的定义求这个正数的值.2. 已知a、b 是m的平方根， 则有a=b或a+b=0.
解:(1)根据题意，得(2a－1)+(a－5)=0，解得a=2， ∴这个正数为(2a－1)2=(2×2－1)2=9.(2)根据题意，分以下两种情况：当2a－1=－a+2 时，a=1，∴ m=(2a－1)2=(2×1－1)2=1.当(2a－1)+(－a+2)=0 时，a=－1，∴ m=(2a－1)2=［2×(－1)－1］2=(－3)2=9.故m 的值为1 或9.
1. 定义：若x2=a，则x叫做a的平方根.2. 性质：一个正数有两个平方根，它们互为相反数， 0的平方根是0，负数没有平方根.3. 平方根与开平方间的关系： (1)开平方是求平方根的运算； (2)平方根是开平方运算的结果.
求一个非负数的平方根的方法：① 求一个非负数a的平方根，就是要把平方后等于a的 数找出来，从而求出a的所有平方根；② 求带分数的平方根时，应先将带分数化为假分数， 这也是常出错的地方.注意：正数的平方根有两个，前面必定有“±”号.