新教材适用2023_2024学年高中数学第1章数列章末整合提升课件北师大版选择性必修第二册

这是一份新教材适用2023_2024学年高中数学第1章数列章末整合提升课件北师大版选择性必修第二册，共33页。

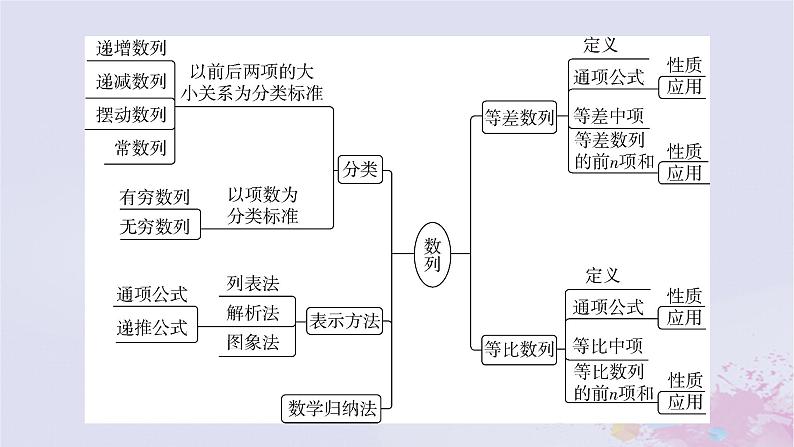
第一章　数　列章末整合提升知识体系构建要点专项突破　　　　(1)已知数列{an}满足an＋1＝3an＋4,a1＝1,则an＝________. (2)已知a1＋2a2＋22a3＋…＋2n－1an＝9－6n，则数列{an}的通项公式是____________________. 3n－2(3)已知公差为d的等差数列{an}的前n项和是Sn，且a2＋a5＝12，S5＝25.①求数列{an}的通项公式；②数列{bn}满足：b1＝2，bn＝bn－1＋2an(n≥2)，求数列{bn}的通项公式．[解析]　(1)根据题意，知数列{an}满足an＋1＝3an＋4，故an＝3n－2.(3)①由a2＋a5＝12，S5＝25，得所以an＝1＋2×(n－1)＝2n－1.②当n≥2时，bn＝bn－1＋2an，则bn－bn－1＝22n－1(n≥2)，又b1＝2，所以bn＝b1＋(b2－b1)＋(b3－b2)＋…＋(bn－bn－1)[规律方法]　数列通项公式的求法(1)定义法，直接利用等差数列或等比数列的定义求通项公式的，这种方法适用已知数列类型的题目．(4)构造法，形如an＋1＝Aan＋b可构造{an＋n}为等比数列，再求通项公式.(1)证明：数列{bn}是等差数列；(2)求{an}的通项公式．[规律方法]　等差、等比数列的判断与证明方法(2)中项公式法：2an＋1＝an＋an＋2⇔{an}是等差数列；a＝an·an＋2 (an≠0)⇔{an}是等比数列；(3)通项公式法：an＝kn＋b(k，b是常数)⇔{an}是等差数列；an＝c·qn(c，q为非零常数)⇔{an}是等比数列；(4)前n项和公式法：Sn＝An2＋Bn(A，B为常数，n∈N*)⇔{an}是等差数列；Sn＝Aqn－A(A，q为常数，且A≠0，q≠0，q≠1，n∈N*)⇔{an}是等比数列．[提醒]　①前两种方法是判定等差、等比数列的常用方法，而后两种方法常用于选择、填空题中的判定．②若要判定一个数列不是等差(比)数列，则只需判定其任意的连续三项不成等差(比)即可.　　　　　(1)(多选)等差数列{an}中，Sn为其前n项和，a1＝15，S5＝S11，则以下说法正确的是(　　　)A．d＝－2B．a6＝－a11C．Sn的最大值为S7D．使得Sn≥0成立的最大整数n＝16(2)在等比数列{an}中，a1＝1，a4＝8，则{an}的公比为_____，{an}的前6项和为_______. ABD263(3)在等差数列{an}中，a2＋a7＝－23，S10＝－145.①求数列{an}的通项公式；②若数列{an＋bn}是首项为1，公比为a的等比数列，求{bn}的前n项和Sn.(2)因为在等比数列{an}中，a1＝1，a4＝8，②因为数列{an＋bn}是首项为1，公比为a的等比数列，所以an＋bn＝an－1，则bn＝an－1＋3n－2，所以Sn＝b1＋b2＋…＋bn＝(a0＋a1＋…＋an－1)＋3(1＋2＋…＋n)－2n.若a＝1，则a0＋a1＋…＋an－1＝n；[规律方法]　等差与等比数列的基本量计算方法在等差(或等比)数列中，首项a1与公差d(或公比q)是两个基本量，一般的等差(或等比)数列的计算问题，都可以设出这两个量求解．在等差数列中的五个量a1，d，n，an，Sn或等比数列中的五个量a1，q，n，an，Sn中，可通过列方程组的方法，知三求二．在利用Sn求an时，要注意验证n＝1是否成立.　　　　　已知{an}为等差数列，前n项和为Sn，数列{bn}是首项为1的等比数列，4b2－b3＝4，b4＝a4＋4a1，2S15＝15b5.(1)求{an}和{bn}的通项公式；(2)求数列{anb2n＋1}的前n项和．[解析]　(1)设等差数列{an}的公差为d，等比数列{bn}的公比为q，由已知4b2－b3＝4，得b1(4q－q2)＝4，而b1＝1，则q2－4q＋4＝0，解得q＝2，所以bn＝2n－1；由b4＝a4＋4a1，得5a1＋3d＝8，由2S15＝15b5，得a1＋7d＝8，联立以上两式解得a1＝d＝1，则an＝1＋1×(n－1)＝n.所以{an}和{bn}的通项公式分别为an＝n，bn＝2n－1.(2)设数列{anb2n＋1}的前n项和为Tn，由anb2n＋1＝n×4n，得Tn＝1×4＋2×42＋3×43＋…＋n×4n，4Tn＝1×42＋2×43＋3×44＋…＋n×4n＋1，[规律方法]　数列求和时，根据数列通项公式特征选择求和法，尤其是涉及等比数列求和时要注意公比q对Sn的影响．一般常见的求和方法有：(1)公式法：利用等差数列或等比数列前n项和公式；(2)分组求和法：把一个数列分成几个可以直接求和的数列；(3)裂项相消法：有时把一个数列的通项公式分成两项差的形式，相加过程消去中间项，只剩有限项再求和；(4)错位相减法：适用于一个等差数列和一个等比数列对应项相乘构成的数列求和；(5)并项求和法：一个数列的前n项和中，可两两结合求解，则称之为并项求和．形如an＝(－1)nf(n)类型，可采用两项合并求解．