第一章 数列 再练一课(范围：§1～§3) 课件+Word版

再练一课(范围：§1～§3)

一、单项选择题

1．在等差数列{an}中，a100＝120，a90＝100，则公差d等于(　　)

A．2  B．20  C．100  D．不确定

答案　A

解析　∵a100－a90＝10d，∴10d＝20，即d＝2.

2．在等比数列{an}中，a3a4a5＝3，a6a7a8＝24，则a9a10a11的值为(　　)

A．48  B．72  C．144  D．192

答案　D

解析　∵＝q9＝8(q为公比)，

∴a9a10a11＝a6a7a8q9＝24×8＝192.

3．已知等差数列的前n项和为Sn，若S13<0，S12>0，则此数列中绝对值最小的项为(　　)

A．第5项   B．第6项

C．第7项   D．第8项

答案　C

解析　由得

所以|a6|－|a7|＝a6＋a7>0，所以|a6|>|a7|.

4．等比数列{an}的公比为q(q≠1)，则数列a3，a6，a9，…，a3n，…的前n项和为(　　)

A.   B.

C.   D.

答案　C

解析　在等比数列中，序号成等差数列，则项仍成等比数列，则a3，a6，…，a3n是等比数列，且首项为a3，公比为＝q3，再用等比数列的前n项和公式求解，即Sn＝.

5．设数列{an}的前n项和为Sn，称Tn＝为数列a1，a2，a3，…，an的“理想数”，已知数列a1，a2，a3，a4，a5的理想数为2 014，则数列2，a1，a2，…，a5的“理想数”为(　　)

A．1 673  B．1 675  C.  D.

答案　D

解析　因为数列a1，a2，…，a5的“理想数”为2 014，所以＝2 014，即S1＋S2＋S3＋S4＋S5＝5×2 014，所以数列2，a1，a2，…，a5的“理想数”为＝＝.

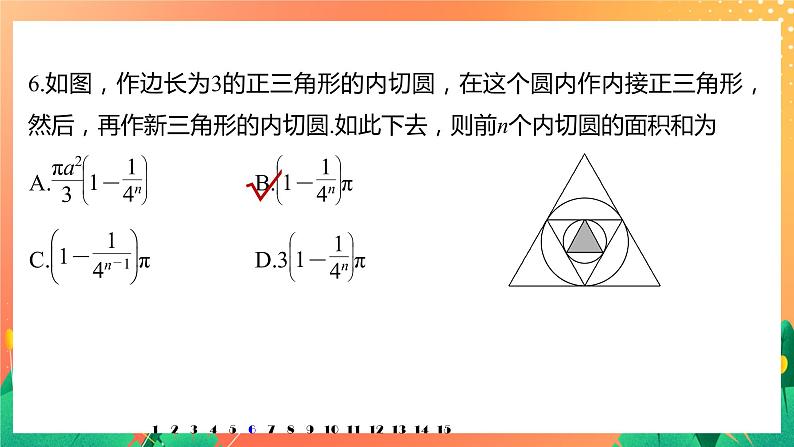
6.如图，作边长为3的正三角形的内切圆，在这个圆内作内接正三角形，然后，再作新三角形的内切圆．如此下去，则前n个内切圆的面积和为(　　)

A.   B.π

C.π   D．3π

答案　B

解析　根据条件第一个内切圆的半径为×3＝，面积为π，第二个内切圆的半径为，面积为π，…，这些内切圆的面积组成一个等比数列，首项为π，公比为，故面积之和为＝π.

二、多项选择题

7．在等比数列{an}中，S2＝7，S6＝91，则S4等于(　　)

A．－28  B．－21  C．21  D．28

答案　BD

解析　∵数列{an}为等比数列，

∴S2，S4－S2，S6－S4成等比数列，

∴(S4－S2)2＝S2(S6－S4)，即(S4－7)2＝7·(91－S4)，

∴S－7S4－588＝0，∴S4＝28或S4＝－21.

8．等差数列{an}的前n项和记为Sn，若a2＋a4＋a15的值为确定的常数，则下列各数中无法确定为常数的是(　　)

A．S7  B．S8  C．S13  D．S15

答案　ABD

解析　a2＋a4＋a15＝a1＋d＋a1＋3d＋a1＋14d＝3(a1＋6d)＝3a7＝3×＝×＝S13，可知S13是常数，其他选项无法确定．

三、填空题

9．一个直角三角形的三边成等比数列，则较小锐角的正弦值是________．

答案　

解析　设三边为a，aq，aq2(q>1)，则(aq2)2＝(aq)2＋a2，

∴q2＝.较小锐角记为θ，则sin θ＝＝＝.

10．在等差数列{an}中，a1>0，d＝，an＝3，Sn＝，则a1＝________，n＝________.

答案　2　3

解析　由

得n2－13n＋30＝0，∴n＝3或n＝10.

又当n＝3时，a1＝2>0；

当n＝10时，a1＝－<0，不符合题意，舍去，

故a1＝2，n＝3.

11．在公差不为零的等差数列{an}中，2a3－a＋2a11＝0，数列{bn}是等比数列，且b7＝a7，则b6b8＝________.

答案　16

解析　∵2a3－a＋2a11＝2(a3＋a11)－a＝4a7－a＝0，

又b7＝a7≠0，∴b7＝a7＝4.∴b6b8＝b＝16.

12．等比数列{an}共有2n项，它的全部各项的和是奇数项的和的3倍，则公比q＝________.

答案　2

解析　设{an}的公比为q，由已知可得q≠1，则奇数项也构成等比数列，其公比为q2，首项为a1，

S2n＝，S奇＝.

由题意得＝，

∴1＋q＝3，∴q＝2.

四、解答题

13．等比数列{an}的前n项和为Sn，已知S1，S3，S2成等差数列．

(1)求{an}的公比q；

(2)若a1－a3＝3，求Sn.

解　(1)依题意有a1＋(a1＋a1q)＝2(a1＋a1q＋a1q2)，

由于a1≠0，故2q2＋q＝0.

又q≠0，从而q＝－.

(2)由已知可得a1－a12＝3，故a1＝4.

从而Sn＝＝.

14.在我国古代，9是数之极，代表尊贵之意，所以中国古代皇家建筑中包含许多与9相关的设计．例如，北京天坛圆丘的地面由扇环形的石板铺成(如图所示)，最高一层的中心是一块天心石，围绕它的第1圈有9块石板，从第2圈开始，每1圈比前1圈多9块，共有9圈，则：

(1)第9圈共有多少块石板？

(2)前9圈一共有多少块石板？

解　(1)设从第1圈到第9圈石板数所成数列为{an}，由题意可知{an}是等差数列，其中a1＝9，d＝9，n＝9.

由等差数列的通项公式，得第9圈石板块数为

a9＝a1＋(9－1)·d＝9＋(9－1)×9＝81(块)．

故第9圈共有81块石板．

(2)由等差数列前n项和公式，得前9圈石板总数为

S9＝9a1＋d＝9×9＋×9＝405(块)．

故前9圈一共有405块石板．

15．已知两个等比数列{an}，{bn}，满足a1＝a(a>0)，b1－a1＝1，b2－a2＝2，b3－a3＝3.

(1)若a＝1，求数列{an}的通项公式；

(2)若数列{an}唯一，求a的值．

解　(1)设{an}的公比为q，则b1＝1＋a1＝1＋a＝2，b2＝2＋aq＝2＋q，b3＝3＋aq2＝3＋q2.

由b1，b2，b3成等比数列，得(2＋q)2＝2(3＋q2)，

即q2－4q＋2＝0，

解得q1＝2＋，q2＝2－，

故{an}的通项公式为an＝(2＋)n－1或an＝(2－)n－1.

(2)设{an}的公比为q，则由(2＋aq)2＝(1＋a)·(3＋aq2)，得aq2－4aq＋3a－1＝0，

由a>0得，Δ＝4a2＋4a>0，

故方程aq2－4aq＋3a－1＝0有两个不同的实根．

由{an}唯一，故方程必有一根为0，代入上式得a＝.