高中数学人教A版 (2019)必修 第一册4.4 对数函数课前预习ppt课件

这是一份高中数学人教A版 (2019)必修 第一册4.4 对数函数课前预习ppt课件，共20页。PPT课件主要包含了预学案，共学案，y＝ax，y＝logax，答案A，log2x，答案B，答案C等内容，欢迎下载使用。

反函数❶1．指数函数________(a>0，且a≠1)和对数函数________(a>0，且a≠1)互为反函数．它们的定义域与值域正好互换．2．互为反函数的两个函数的图象关于直线y＝x对称．
【即时练习】　1．下列函数中，与函数y＝lg x互为反函数的是(　　)A．y＝10x B．y＝10－xC．y＝－lg x D．y＝lg (－x)
解析：由y＝lg x得x＝10y，对换x，y的位置可得y＝lg x的反函数为y＝10x，所以与函数y＝lg x互为反函数的是y＝10x.故选A.
2．函数y＝f(x)的图象与y＝2x的图象关于直线y＝x对称，则函数f(x)＝________．
解析：∵函数y＝f(x)的图象与y＝2x的图象关于直线y＝x对称，∴y＝f(x)是y＝2x的反函数，由y＝2x得x＝lg2y，将x与y互换，可得y＝lg2x，即f(x)＝lg2x.
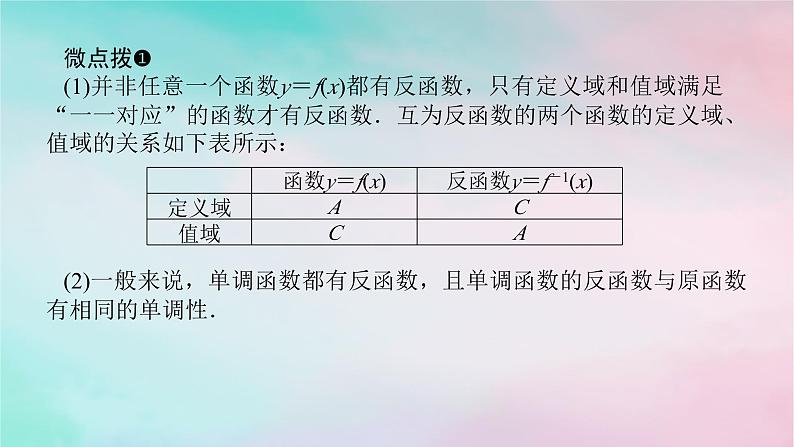
微点拨❶(1)并非任意一个函数y＝f(x)都有反函数，只有定义域和值域满足“一一对应”的函数才有反函数．互为反函数的两个函数的定义域、值域的关系如下表所示：(2)一般来说，单调函数都有反函数，且单调函数的反函数与原函数有相同的单调性．
【学习目标】　(1)进一步掌握对数函数的图象和性质．(2)了解反函数的概念和图象特点．
题型 1 反函数【问题探究】　在同一坐标系下，画出函数y＝2x与y＝lg2x的图象，观察两个函数图象的关系．
提示：两个函数图象关于直线y＝x对称．
例1　已知函数f(x)是函数y＝ax(a>0，且a≠1)的反函数，且f(x)的图象过点(5，2)，则a＝________.
学霸笔记：(1)现行教材反函数只要求同底数的指数函数与对数函数． (2)互为反函数的两个函数具有相同的单调性，图象关于直线y＝x对称，定义域与值域互换．
题型 2 对数型函数的值域(最值)例2　已知函数f(x)＝lg2(x－4)－lg2(x－2)．(1)求f(x)的定义域；(2)求f(x)的值域．
题后师说求对数型函数y＝lgaf(x)(a＞0，且a≠1)的值域(最值)的步骤
跟踪训练2　已知函数f(x)＝lga(3－x)＋lga(x＋3)(0题型 3 对数函数性质的综合应用例3　已知函数f(x)＝lga(5＋x)－lga(5－x)(a>0，且a≠1)．(1)求函数f(x)的定义域；(2)判断函数f(x)的奇偶性并给出证明；(3)求使f(x)>0成立的x的取值范围．
学霸笔记对数函数的综合问题，常以对数函数为依托，着重考虑对数的运算、对数函数的图象与性质、函数的单调性、奇偶性、值域与最值等，熟悉对数函数的图象与性质及求解函数问题的一般规律和方法是解答这类问题的前提．
2．函数y＝lg3x的反函数为y＝f(x)，则f(2)＝(　　)A．9 B．18C．32 D．36
解析：函数y＝lg3x的反函数为f(x)＝3x，所以f(2)＝32＝9，故选A.
3．函数f(x)＝lg2(3x＋1)的值域为(　　)A．(0，＋∞) B．[0，＋∞)C．(1，＋∞) D．[1，＋∞)
解析：∵3x>0，∴3x＋1>1，∴lg2(3x＋1)>0，∴函数f(x)的值域为(0，＋∞)．故选A.
4．若函数f(x)＝lgax(a>0，且a≠1)在区间[2，4]上的最大值与最小值之差为2，则a＝________．