






- 2024版新教材高中数学第四章指数函数与对数函数4.4对数函数4.4.3不同函数增长的差异课件新人教A版必修第一册 课件 0 次下载
- 2024版新教材高中数学第四章指数函数与对数函数4.5函数的应用二4.5.1函数的零点与方程的解课件新人教A版必修第一册 课件 0 次下载
- 2024版新教材高中数学第四章指数函数与对数函数4.5函数的应用二4.5.3函数模型的应用课件新人教A版必修第一册 课件 0 次下载
- 2024版新教材高中数学第四章指数函数与对数函数习题课指数型函数对数型函数的性质的综合应用课件新人教A版必修第一册 课件 0 次下载
- 2024版新教材高中数学第四章指数函数与对数函数章末复习课课件新人教A版必修第一册 课件 0 次下载
高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)多媒体教学课件ppt
展开一、二分法❶对于在区间[a,b]上图象连续不断且__________的函数y=f(x),通过不断地把函数f(x)的零点所在的区间__________,使所得区间的两个端点逐步逼近________,进而得到零点近似值的方法叫做二分法.
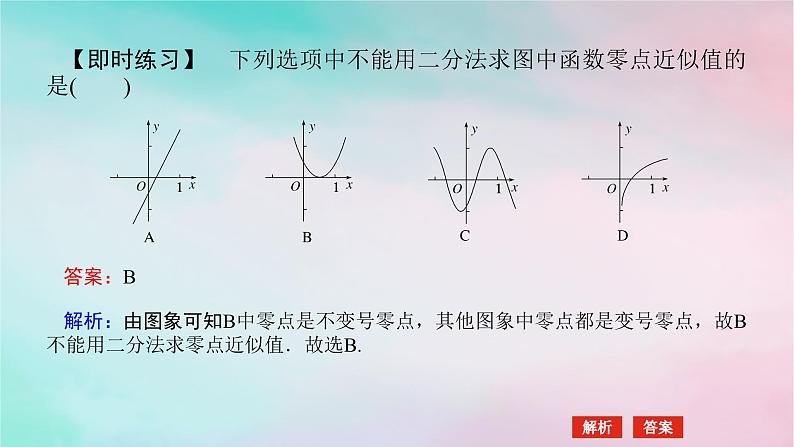
【即时练习】 下列选项中不能用二分法求图中函数零点近似值的是( )
解析:由图象可知B中零点是不变号零点,其他图象中零点都是变号零点,故B不能用二分法求零点近似值.故选B.
微点拨❶二分法的依据是零点存在定理,仅适用于函数的变号零点(函数图象通过零点时函数值的符号变号,如求函数f(x)=(x-1)2的零点近似值就不能用二分法).
二、用二分法求方程的近似解❷给定精确度ε,用二分法求函数y=f(x)零点x0的近似值的一般步骤:第一步:确定零点x0的初始区间[a,b],验证f(a)f(b)<0.第二步:求区间(a,b)的中点c.第三步:计算f(c),并进一步确定零点所在的区间:(1)若f(c)=0(此时x0=c),则c就是函数的零点;(2)若f(a)f(c)<0,则令b=c(此时零点x0∈(a,c));(3)若f(c)f(b)<0,则令a=c(此时零点x0∈(c,b)).第四步:判断是否达到精确度ε,即若|a-b|<ε,则得到零点近似值a(或b),否则重复第二步至第四步.
微点拨❷(1)用二分法求函数零点的近似值时,要根据函数的性质尽可能地找到含有零点的更小的区间,这样可以减少用二分法的次数,减少计算量.(2)二分法采用逐步逼近的思想,使区间逐步缩小,使函数零点所在的范围逐步缩小,也就是逐渐逼近函数的零点.当区间长度小到一定程度时,就得到近似值.
(3)由|a-b|<ε,可知区间[a,b]中任意一个值都是零点x0的满足精确度ε的近似值.为了方便,这里统一取区间端点a(或b)作为零点的近似值.“精确度”与“精确到”是不一样的概念.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后保留一位小数得1.3.“精确度为0.1”是指零点近似值所在区间[a,b]满足|a-b|<0.1,比如零点近似值所在区间是[1.25,1.34].若精确度为0.1,则近似值可以是1.25,也可以是1.34.(4)由函数的零点与相应方程的根的关系,我们可用二分法来求方程的近似解.对于求形如f(x)=g(x)的方程的近似解,可以通过移项转化成求形如F(x)=f(x)-g(x)=0的方程的近似解,然后按照用二分法求函数F(x)零点近似值的步骤求解.
【即时练习】 1.判断正误(正确的画“√”,错误的画“×”)(1)用二分法可求所有函数零点的近似值.( )(2)用二分法求方程的近似解时,可以精确到小数点后的任一位.( )(3)只有在求函数的零点时才用二分法.( )
2.设f(x)=3x+3x-8,现用二分法求关于x的方程3x+3x-8=0在区间(1,2)内的近似解,已知f(1)<0,f(1.25)<0,f(1.5)>0,f(2)>0,则方程的根落在区间( )A.(1,1.25) B.(1.25,1.5)C.(1.5,2) D.不能确定
解析:因为f(1)<0,f(2)>0,且f(x)的图象在(1,2)上连续,所以f(x)在(1,2)上至少存在一个零点,因为f(1.5)>0,所以f(x)在(1,1.5)上存在零点,因为f(1.25)<0,所以f(x)在(1.25,1.5)上存在零点,所以方程的根落在区间(1.25,1.5)内,故选B.
【学习目标】 (1)通过具体实例理解二分法的概念及其使用条件.(2)根据具体函数,用二分法求相应方程的近似解.(3)在用二分法求方程近似解的同时,感受近似思想,逼近思想等数学思想的含义和作用.
题型 1 二分法概念的理解【问题探究1】 有16个大小相同,颜色相同的金币,其中有15个金币是真的,有一个质量稍轻的是假的.用天平称几次一定可以找出这个稍轻的假币?
提示:4次第一次,两端各放8个金币,高的那一端一定有假币;第二次,两端各放4个金币,高的那一端一定有假币;第三次,两端各放2个金币,高的那一端一定有假币;第四次,两端各放1个金币,高的那一端一定是假币.
例1 下列函数图象与x轴都有公共点,其中不能用二分法求图中函数零点近似值的是( )
解析:根据题意,利用二分法求函数零点的条件是:函数在零点的左右两侧的函数值符号相反,即穿过x轴,据此分析选项:A选项中函数不能用二分法求零点,故选A.
学霸笔记:运用二分法求函数的零点应具备的条件(1)函数图象在零点附近连续不断.(2)在该零点左右函数值异号.只有满足上述两个条件,才可用二分法求函数零点.
解析:由图象可知,在x=x2附近,函数f(x)均大于0,故x2不能用二分法求出.其他零点附近函数值符号均变号,可以用二分法求解.故选B.
题型 2 用二分法求函数零点的近似解【问题探究2】 假设已知函数f(x)=ex-3x的零点在区间(1,2)内,如何缩小零点所在区间的范围?
提示:取区间(1,2)的中点值1.5;计算f(1.5)的值,验证f(1.5)f(2)<0是否成立,若成立,则f(x)的零点在区间(1.5,2)内,否则在区间(1,1.5)内.
例2 用二分法求2x+x=4在区间(1,2)内的近似解(精确度0.2).参考数据:
解析:令f(x)=2x+x-4,则f(1)=2+1-4=-1<0,f(2)=22+2-4=2>0.∵|1.375-1.5|=0.125<0.2,∴2x+x=4在(1,2)内的近似解可取为1.375.
学霸笔记:用二分法求函数零点近似值的步骤可以概括如下
跟踪训练2 (1)已知函数f(x)=ln (x+2)+2x-m的一个零点附近的函数值的参考数据如下表:由二分法,方程ln (x+2)+2x-m=0的近似解(精确度为0.05)可能是( )A.0.625 B.-0.009C.0.562 5 D.0.066
解析:由题意得f(x)=ln (x+2)+2x-m在区间(0,+∞)上单调递增,设方程ln (x+2)+2x-m=0的解的近似值为x0,由表格得f(0.531 25)f(0.562 5)<0,所以x0∈(0.531 25,0.562 5),因为|0.531 25-0.562 5|=0.031 25<0.05,所以方程的近似解可取为0.562 5.故选C.
(2)用“二分法”求函数y=f(x)零点的近似值时,若第一次所取的区间是[0,m],则第三次所取的区间可能是________.(只需写出满足条件的一个区间即可)
随堂练习1.观察下列函数的图象,判断能用二分法求其零点的是( )
解析:由图象可知,BD选项中函数无零点,AC选项中函数有零点,C选项中函数零点两侧函数值符号相同,A选项中函数零点两侧函数值符号相反,故A选项中函数零点可以用二分法求近似值,C选项不能用二分法求零点.故选A.
2.下列函数中不能用二分法求零点近似值的是( )A.f(x)=3x-1 B.f(x)=x3C.f(x)=|x| D.f(x)=ln x
解析:根据题意,依次分析选项:对于A,f(x)=3x-1在R上是单调函数,有唯一零点,且函数值在零点两侧异号,可用二分法求零点;对于B,f(x)=x3在R上是单调函数,有唯一零点,且函数值在零点两侧异号,可用二分法求零点;对于C,f(x)=|x|,虽然也有唯一的零点,但函数值在零点两侧都是正号,故不能用二分法求零点;对于D,f(x)=ln x在(0,+∞)上是单调函数,有唯一零点,且函数值在零点两侧异号,可用二分法求零点.故选C.
3.已知函数f(x)=x-e-x的部分函数值如下表所示那么函数f(x)的一个零点的近似值(精确度为0.01)为( )A.0.55 B.0.57C.0.65 D.0.7
4.利用二分法求f(x)=x3-2的零点时,第一次确定的区间是(1,2),第二次确定的区间是________.
人教A版 (2019)必修 第一册4.5 函数的应用(二)课文配套课件ppt: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000277_t3/?tag_id=26" target="_blank">4.5 函数的应用(二)课文配套课件ppt</a>,共19页。PPT课件主要包含了连续不断,一分为二,c就是函数的零点,a-b<ε,探究一二分法的概念等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.5 函数的应用(二)授课课件ppt: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000277_t3/?tag_id=26" target="_blank">4.5 函数的应用(二)授课课件ppt</a>,共19页。PPT课件主要包含了连续不断,一分为二,c就是函数的零点,a-b<ε,探究一二分法的概念等内容,欢迎下载使用。
人教A版 (2019)必修 第一册4.5 函数的应用(二)课文内容课件ppt: 这是一份人教A版 (2019)必修 第一册4.5 函数的应用(二)课文内容课件ppt,共32页。PPT课件主要包含了素养·目标定位,课前·基础认知,课堂·重难突破,随堂训练等内容,欢迎下载使用。













