数学必修 第一册3.4 函数的应用（一）教案配套ppt课件

这是一份数学必修 第一册3.4 函数的应用（一）教案配套ppt课件，共38页。PPT课件主要包含了预学案，共学案，常见的函数模型❶，kx＋b，ax2＋bx＋c，答案B，答案C，y＝100x－40，答案A等内容，欢迎下载使用。

微点拨❶(1)在函数模型中，二次函数模型占有重要的地位．可利用配方法、换元法、单调性法等方法求最值，从而解决实际问题中的利润最大、用料最省等最值问题．(2)建立分段函数模型的关键是确定分段的各边界点，即明确自变量的取值区间，对每一区间进行分类讨论，从而写出函数的解析式．
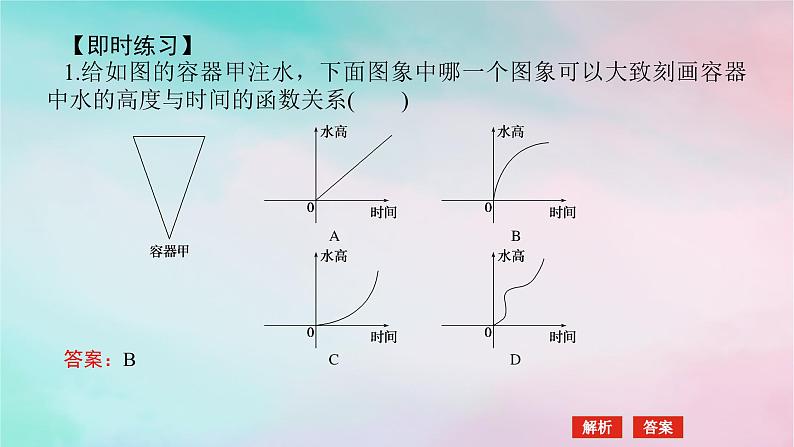
【即时练习】　1.给如图的容器甲注水，下面图象中哪一个图象可以大致刻画容器中水的高度与时间的函数关系(　　)
解析：容器下端较窄，上端较宽，当均匀的注入水时，刚开始的一段时间高度变化较快，随着时间的推移，高度的变化速度开始减慢，即高度变化不太明显，四个图象中只有B项符合特点．故选B.
2．某机器总成本y(万元)与产量x(台)之间的函数关系式是y＝x2－75x，若每台机器售价为25万元，则该厂获利润最大时应生产的机器台数为(　　)A．30　　　　B．40　　　　C．50　　　　D．60
解析：设安排生产x台，则获得利润f(x)＝25x－y＝－x2＋100x＝－(x－50)2＋2 500.故当x＝50台时，获利润最大．故选C.
3.一辆汽车在行驶过程中，路程y(千米)与时间x(小时)之间的函数关系如图所示，当0≤x≤1时，y关于x的函数解析式为y＝60x，当1≤x≤2时，y关于x的函数解析式为___________．
【学习目标】　(1)初步体会一次函数、二次函数、幂函数、分段函数模型的广泛应用．(2)能将实际问题转化为熟悉的模型，建立合适的数学模型解决简单的实际问题．
题型 1 一次函数模型的应用例1　为了发展电信事业，方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费用y(元)的关系如图所示．(1)分别求出通话费用y1，y2与通话时间x之间的函数解析式；(2)请帮助用户计算在一个月内使用哪种卡便宜．
跟踪训练1　某列火车从北京西站开往石家庄，全程277 km.火车出发10 min开出13 km，之后以120 km/h的速度匀速行驶．试写出火车行驶的总路程s(km)与匀速行驶的时间t(h)之间的函数关系式，并求火车离开北京2 h时火车行驶的路程．
题型 2 二次函数模型的应用例2　某超市经销一种销售成本为每件40元的商品．据市场调查分析，如果按每件50元销售，一周能售出500件；若销售单价每涨1元，每周销量就减少10件．设销售单价为x元(x≥50)，一周的销售量为y.(1)写出y与x的函数关系式；(2)设一周的销售利润为S，写出S与x的函数关系式，并确定当单价在什么范围内变化时，利润随着单价的增大而增大？(3)在超市对该种商品投入不超过10 000元的情况下，使得一周销售利润达到8 000元，销售单价应定为多少？
解析：(1)根据题意，按每件50元销售，一周售出500件，若销售单价每涨1元，每周销售量就减少10件，可得y与x的函数关系式为y＝500－10(x－50)＝1 000－10x，x∈[50，100].(2)由题意，可得S＝(x－40)y＝(x－40)(1 000－10x)＝－10x2＋1 400x－40 000＝－10(x－70)2＋9 000，当x∈[50，70]时，利润随着单价的增大而增大．(3)由题意，令S＝8 000，可得－10x2＋1 400x－40 000＝8 000，解得x＝60或x＝80.当x＝60时，成本＝40×[500－10(60－50)]＝16 000＞10 000不符合要求，舍去；当x＝80时，成本＝40×[500－10(80－50)]＝8 000＜10 000符合要求．所以销售单价应定为80元，才能使一周销售利润达到8 000元的同时，投入不超过10 000元．
学霸笔记：二次函数模型的应用根据实际问题建立二次函数模型后，可利用配方法、换元法以及函数的单调性等方法求最值，从而解决实际问题中的利润最大、用料最省等最值问题．
跟踪训练2　如图，某中学准备在校园里利用院墙的一段，再砌三面墙，围成一个矩形花园ABCD，已知院墙MN长为25米，篱笆长50米(篱笆全部用完)，设篱笆的一面AB的长为x米．(1)当AB的长为多少米时，矩形花园的面积为300平方米？(2)若围成的矩形ABCD的面积为 S 平方米，当 x 为何值时， S 有最大值，最大值是多少？
解析：(1)设篱笆的一面AB的长为 x 米，则BC＝(50－2x)m，由题意得，x(50－2x)＝300，解得x1＝15，x2＝10，∵50－2x≤25，∴x≥12.5，∴x＝15，∴AB的长为15米时，矩形花园的面积为300平方米．(2)由题意得，S＝x(50－2x)＝－2x2＋50x＝－2(x－12.5)2＋312.5，12.5≤x<25，∴x＝12.5时， S 取得最大值，此时，S＝312.5，∴当 x 为12.5米时， S 有最大值，最大值是312.5平方米．
题后师说应用分段函数时的三个关注点
跟踪训练3　某厂生产某种零件，每个零件的成本为30元，出厂单价定为52元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于41元．(1)当一次订购量为多少个时，零件的实际出厂单价恰好降为41元？(2)设一次订购量为x个，零件的实际出厂单价为P元，写出函数P＝f(x)的表达式；(3)当销售商一次订购500个零件时，该厂获得的利润是多少元？(工厂售出一个零件的利润＝实际出厂单价－成本)
随堂练习1.在自然界中，某种植物生长发育的数量y与时间x的关系如下表所示：下面的函数关系式中，能表达这种关系的是(　　)A．y＝2x－1 B．y＝x2－1C．y＝2x＋1 D．y＝1.5x2－2.5x＋2
解析：根据表中数据可判断函数为一次函数，将各数据代入y＝2x－1中均成立，故选A.
2．国内快递1 000 g以内的包裹的邮资标准如下表：如果某人在西安要快递800 g的包裹到距西安1 200 km的某地，那么他应付的邮资是(　　)A．5.00元 B．6.00元C．7.00元 D．8.00元
解析：通过邮资标准表可得到，当x＝1 200时，y＝7.00元．故选C.
3．某企业一个月生产某种商品x万件时的生产成本为C(x)＝x2＋4x＋10(万元)，一万件售价是30万元，若商品能全部卖出，则该企业一个月生产该商品的最大利润为(　　)A．139万元 B．149万元C．159万元 D．169万元
解析：利润L(x)＝30x－(x2＋4x＋10)＝－x2＋26x－10＝－(x－13)2＋159，故最大利润为159万元．故选C.
4．某药厂研制出一种新型药剂，投放市场后其广告投入x(万元)与药品利润y(万元)存在的关系为y＝xα(α为常数)，其中x不超过5万元．已知去年投入广告费用为3万元时，药品利润为27万元，若今年广告费用投入5万元，预计今年药品利润为________万元．
解析：由已知投入广告费用为3万元时，药品利润为27万元，代入y＝xα中，即3α＝27，解得α＝3，故函数关系式为y＝x3.所以当x＝5时，y＝125.