





2020-2021学年第三章 函数概念与性质3.4 函数的应用(一)授课课件ppt
展开1 | 几类常见的函数模型
2 | 利用函数模型解决实际问题的过程
1.解决某一实际问题的函数模型是唯一的. ( ✕ )2.对于一个实际问题,收集到的数据越多,建立的函数模型的模拟效果越好. ( √ )3.在实际问题中,若变量间的对应关系不能用一个关系式给出,则需构建分段函数 模型. ( √ )
1 | 如何解决已知函数模型的实际应用问题
在实际问题中,大多涉及的两个变量之间的关系符合已知函数模型,如一次函 数、二次函数、反比例函数、幂函数等,解决这种函数应用问题的常见步骤如 下:1.利用待定系数法求出函数解析式;2.根据函数解析式,结合题中需要研究的函数的性质解决实际问题.在函数模型中,二次函数模型占有重要的地位.在根据实际问题得到二次函数的 解析式后,可以利用配方法、换元法、函数的单调性等来求函数的最值,从而解 决实际问题中的利润最大、用料最省等问题.
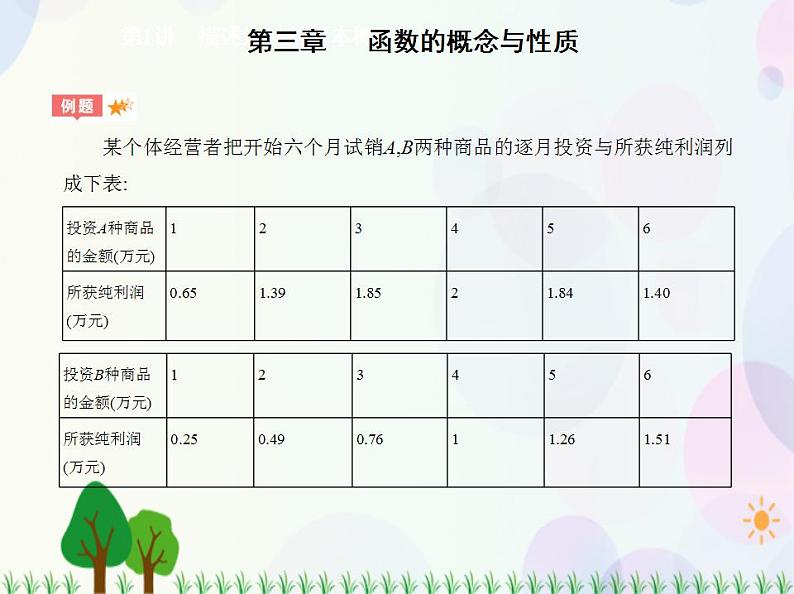
某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列 成下表:
该经营者准备下月投入12万元经营这两种商品,请你帮忙制订一个资金投入 方案,使该经营者获得最大纯利润,并按你的方案求出该经营者下月可获得的最 大纯利润(结果保留两位有效数字).
思路点拨利用已知数据画出散点图,根据散点图的形状选择函数模型,结合条件求出函数 的解析式及定义域,最后由函数的解析式解决相关问题.
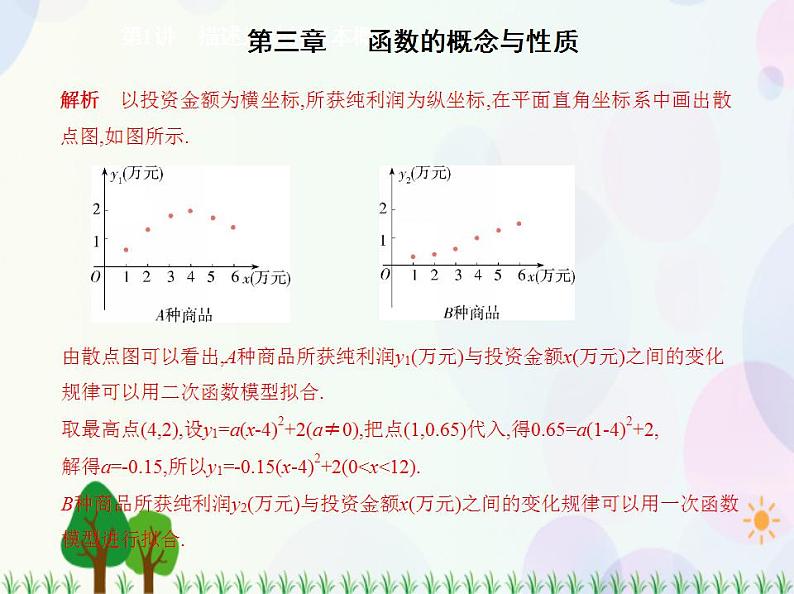
解析 以投资金额为横坐标,所获纯利润为纵坐标,在平面直角坐标系中画出散 点图,如图所示.
由散点图可以看出,A种商品所获纯利润y1(万元)与投资金额x(万元)之间的变化规律可以用二次函数模型拟合.取最高点(4,2),设y1=a(x-4)2+2(a≠0),把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.15,所以y1=-0.15(x-4)2+2(0
1.解决未知函数模型的实际问题时,主要抓住四点:求什么,设什么,列什么,限制什么.(1)“求什么”就是弄清楚要解决什么问题,完成什么任务,通常表现为求函数值.(2)“设什么”就是弄清楚这个问题中有哪些变化因素,找出变化的根源,通常设 变化的根源为自变量.(3)“列什么”就是从函数值出发逐步应用公式,用自变量与已知量表示函数值, 直至求出函数解析式.(4)“限制什么”就是指自变量应满足的限制条件,不仅要考虑自变量是否有意 义,还要考虑用自变量表示的所有其他量是否有意义,另外还要考虑变量的实际 含义,如整数解等.
2.建立函数模型解决实际问题的步骤:(1)设恰当的变量:研究实际问题中量与量之间的关系,确定变量之间的关系,可用 x,y分别表示问题中的变量;(2)建立函数模型:将变量y表示成x的函数,注意函数的定义域;(3)求解函数模型;(4)给出实际问题的解.
要在墙上开一个上部分为半圆,下部分为矩形的窗户(如图),在窗框为定长l 的条件下,要使窗户的透光面积S最大,窗户应具有怎样的尺寸?
思路点拨选择适当的自变量与函数值,利用各量之间的关系求出函数的解析式与定义域, 从而解决问题.
解析 由题意得窗框总长l= x+x+2y,∴y= ,∴S= x2+xy= x2+x· =- + .由 可得x∈ .所以当x= 时,S取得最大值,此时y= .
所以当x= ,y= 时,窗户的透光面积最大.
易错警示解题时要注意求定义域时,不仅要使自变量表示的量有意义(如本题中x>0),还要 使用自变量表示的其他量有意义 .
3 |如何利用分段函数解决实际应用问题
1.在一些实际问题中,函数值与自变量的对应关系随着自变量的取值不同而不同,如:分段计费、分段税率等问题,解决此类问题常需构造分段函数模型,利用分段函数解决问题.2.应用分段函数时的三个注意点:(1)分段函数的“段”一定要分得合理,即对自变量的分类要不重不漏;(2)分段函数的定义域是每一段自变量取值范围的并集;(3)分段函数的值域的求法:逐段求函数值的范围,最后再求各段范围的并集得到 函数的值域.3.利用分段函数解决实际问题时,先在自变量的每段取值中解决相应的问题,再综 合各段的结论,得到问题的解.
经市场调查,某新开业的商场在过去一个月内(以30天计),顾客人数f(t)(千)与 时间t(天)的函数关系近似满足f(t)=4+ (t∈N*),人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)= (1)求该商场的日收益w(t)(千元)与时间t(天)(1≤t≤30,t∈N*)的函数解析式;(2)求该商场日收益(千元)的最小值.
人教A版 (2019)必修 第一册3.4 函数的应用(一)图片课件ppt: 这是一份人教A版 (2019)必修 第一册3.4 函数的应用(一)图片课件ppt,共23页。PPT课件主要包含了题型二二次函数模型,题型三幂函数模型,题型四分段函数模型等内容,欢迎下载使用。
数学3.4 函数的应用(一)教学演示课件ppt: 这是一份数学3.4 函数的应用(一)教学演示课件ppt,共17页。PPT课件主要包含了税率与速算扣除数见表,所以函数解析式为,方法总结,达标检测等内容,欢迎下载使用。
人教A版 (2019)必修 第一册3.4 函数的应用(一)教学ppt课件: 这是一份人教A版 (2019)必修 第一册3.4 函数的应用(一)教学ppt课件,共24页。













