人教部编办版九年级数学上册第二十四章第23课切线长定理含解析答案 试卷

这是一份人教部编办版九年级数学上册第二十四章第23课切线长定理含解析答案，共43页。

第二十四章第23课切线长定理
学校:___________姓名：___________班级：___________考号：___________

一、单选题
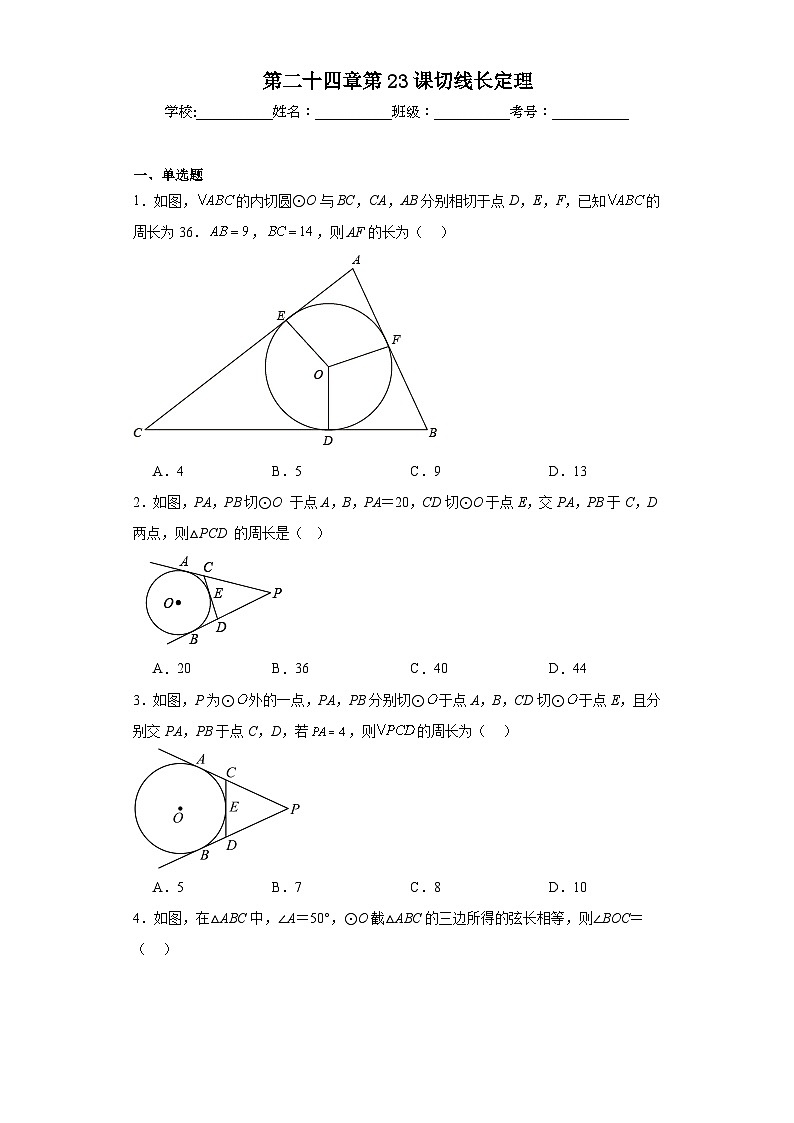
1．如图，的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，已知的周长为36．，，则AF的长为（    ）

A．4 B．5 C．9 D．13
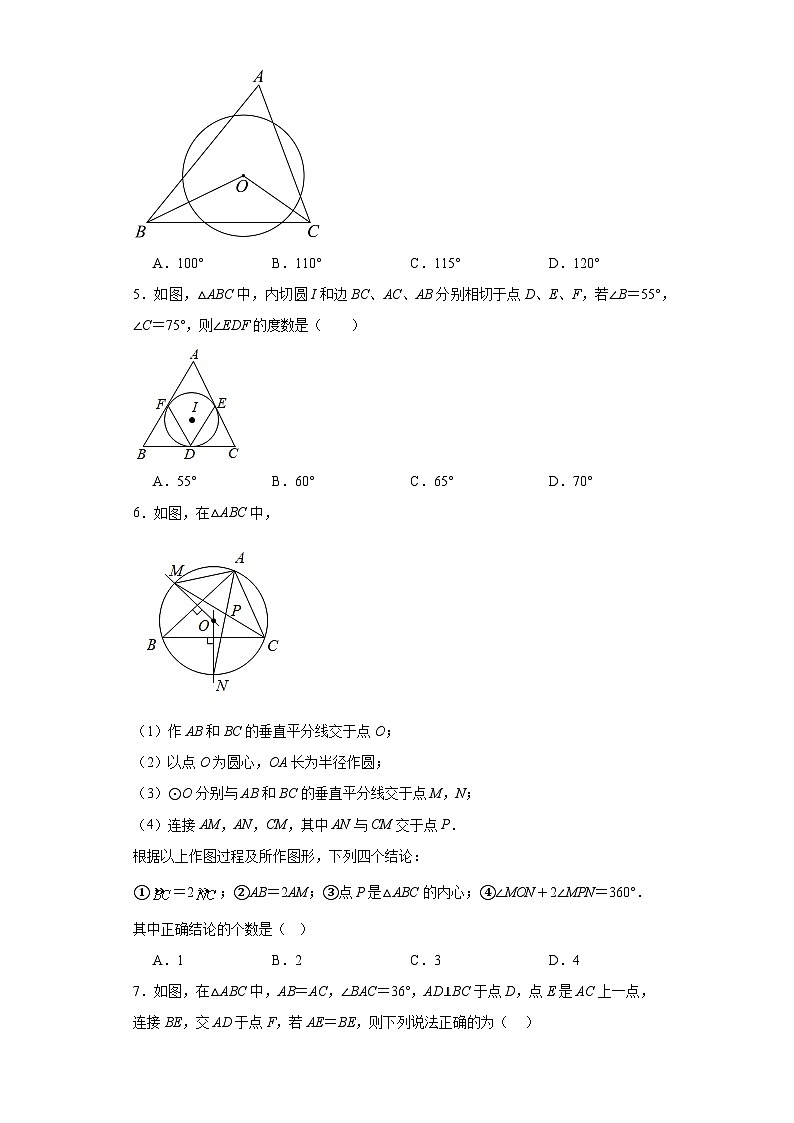
2．如图，PA，PB切⊙O 于点A，B，PA＝20，CD切⊙O于点E，交PA，PB于C，D两点，则△PCD 的周长是（   ）

A．20 B．36 C．40 D．44
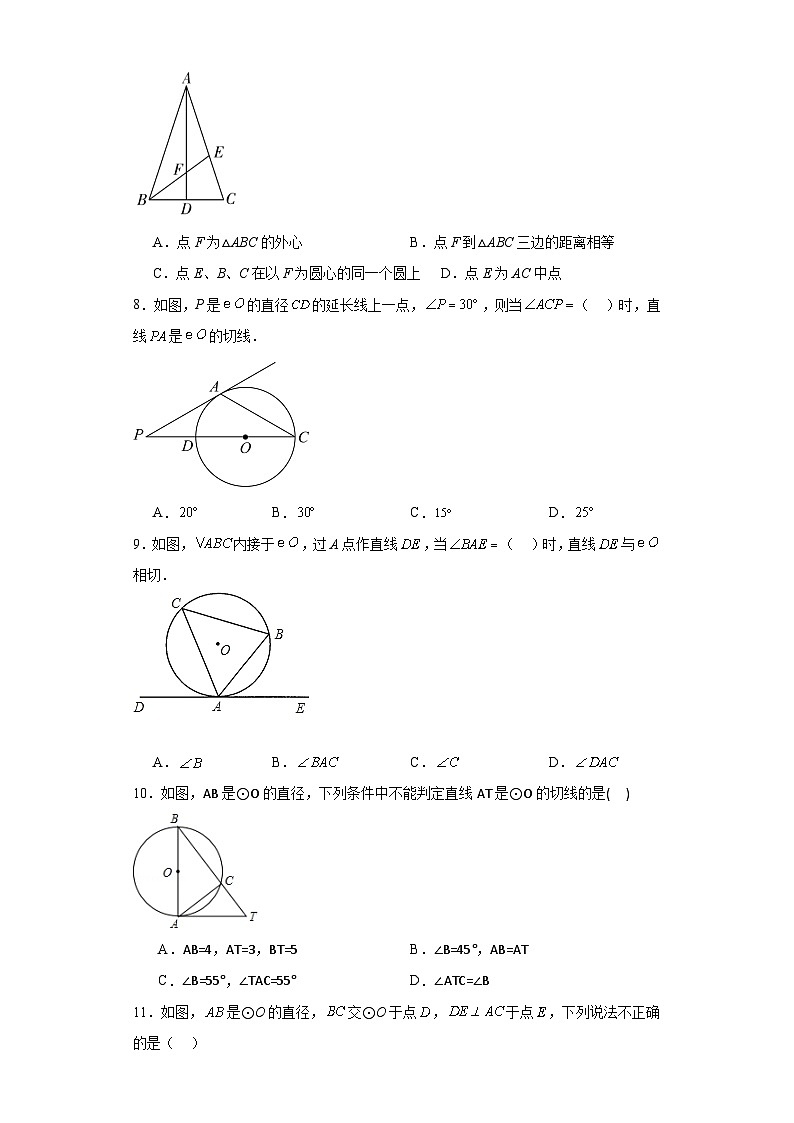
3．如图，P为⊙外的一点，PA，PB分别切⊙于点A，B，CD切⊙于点E，且分别交PA，PB于点C，D，若，则的周长为（    ）

A．5 B．7 C．8 D．10
4．如图，在△ABC中，∠A＝50°，⊙O截△ABC的三边所得的弦长相等，则∠BOC＝（    ）

A．100° B．110° C．115° D．120°
5．如图，△ABC中，内切圆I和边BC、AC、AB分别相切于点D、E、F，若∠B＝55°，∠C＝75°，则∠EDF的度数是（　　）

A．55° B．60° C．65° D．70°
6．如图，在△ABC中，

（1）作AB和BC的垂直平分线交于点O；
（2）以点O为圆心，OA长为半径作圆；
（3）⊙O分别与AB和BC的垂直平分线交于点M，N；
（4）连接AM，AN，CM，其中AN与CM交于点P．
根据以上作图过程及所作图形，下列四个结论：
①＝2；②AB＝2AM；③点P是△ABC的内心；④∠MON＋2∠MPN＝360°．
其中正确结论的个数是（   ）
A．1 B．2 C．3 D．4
7．如图，在△ABC中，AB＝AC，∠BAC＝36°，AD⊥BC于点D，点E是AC上一点，连接BE，交AD于点F，若AE＝BE，则下列说法正确的为（    ）

A．点F为△ABC的外心 B．点F到△ABC三边的距离相等
C．点E、B、C在以F为圆心的同一个圆上 D．点E为AC中点
8．如图，P是的直径的延长线上一点，，则当（    ）时，直线是的切线．

A． B． C． D．
9．如图，内接于，过A点作直线，当（    ）时，直线与相切．


A． B． C． D．
10．如图，AB是⊙O的直径，下列条件中不能判定直线AT是⊙O的切线的是(    )

A．AB=4，AT=3，BT=5 B．∠B=45°，AB=AT
C．∠B=55°，∠TAC=55° D．∠ATC=∠B
11．如图，是⊙O的直径，交⊙O于点，于点，下列说法不正确的是（    ）

A．若，则是⊙O的切线 B．若，则是⊙O的切线
C．若，则是⊙O的切线 D．若是⊙O的切线，则
12．如图，从⊙O外一点P引圆的两条切线PA，PB，切点分别是A，B，若∠APB＝60°，PA＝5，则弦AB的长是（　　）

A． B． C．5 D．5
13．下列直线是圆的切线的是（       ）
A．与圆有公共点的直线 B．到圆心的距离等于半径的直线
C．到圆心的距离大于半径的直线 D．到圆心的距离小于半径的直线
14．如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，连接BD，BE，CE，若∠CBD=32°，则∠BEC的度数为（    ）
  
A．128° B．126° C．122° D．120°
15．下列命题：①平⾏四边形是中⼼对称图形，也是轴对称图形；②直径是最长的弦，半径是最短的弦；③过切点的直线是圆的切线；④三角形的外⼼是三条边垂直平分线的交点；⑤三角形的内⼼是三条内角平分线的交点；其中正确的有（       ）
A．1个 B．2个 C．3个 D．4个
16．如图，AB、BC、CD、DA都是⊙O的切线．已知AD＝3，BC＝6，则AB＋CD的值是(    )

A．3 B．6 C．9 D．12
17．已知三角形的周长为12，面积为6，则该三角形内切圆的半径为（   ）
A．4 B．3 C．2 D．1
18．下列命题中：①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③垂直于半径的直线是圆的切线；④E，F是∠AOB的两边OA，OB上的两点，则不同的E，O，F三点确定一个圆：其中正确的有（    ）
A．个 B．个 C．个 D．0个
19．如图，是的切线，是切点，若，则（    ）

A． B． C． D．都不对
20．如图：切于，切于，交于，下列结论中错误的是（    ）

A． B． C． D．是的中点
21．小明同学用一把直尺和一个直角三角板（有一个锐角为60°）测量一张光盘的直径，他把直尺、三角板和光盘按如图的方式放置，点A是60°角顶点，B是光盘与直尺的公共点，测得AB＝3，则此光盘的直径为（    ）

A．3 B． C． D．
22．如图，在△ABC中，以A为圆心，任意长为半径画弧，分别交AB、AC于点M、N；再分别以M、N为圆心，大于的长为半径画弧，两弧交于点P；连结AP并延长交BC于点D．则下列说法正确的是（    ）

A． B．
C．一定经过△ABC的内心 D．AD一定经过△ABC的外心
23．如图，在中，点为的内心，点在边上，且，若，，则的度数为（    ）

A．111° B．130° C．172° D．170°
24．如图，AB是的直径，PA与相切于点A，交于点C．若，则的度数为（    ）

A． B． C． D．
25．如图，AB为的直径，延长AB到点P，过点P作的切线PC，PD，切点分别为C，D，连接CD交AP于点M，连接BD，AD．若，，则AD的长为（    ）

A． B． C．2 D．
26．如图，BC是⊙O的直径，点A是⊙O上的一点，点D是△ABC的内心，若BC＝5，AC＝3，则BD的长度为（　　）

A．2 B．3 C． D．
27．如图，P为⊙O外一点，PA、PB分别切⊙O于点A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝8，则△PCD的周长为(   )

A．8 B．12 C．16 D．20
28．如图，若等边△ABC的内切圆的半径是2，则△ABC的面积是（    ）

A． B． C． D．
29．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点C作CF∥AB，在CF上取一点E，使DE＝DC，连接BE．对于下列结论：
①BD＝DC；②△CAB∽△CDE；③＝；④BE为⊙O的切线，
其中一定正确的是（　　）

A．①② B．①②③ C．①④ D．①②④

二、填空题
30．如图，PA、PB是⊙O的切线，若∠APO＝25°，则∠BPA＝ ．

31．如图，P是⊙O外一点，PA、PB分别和⊙O切于A、B，C是弧AB上任意一点，过C作⊙O的切线分别交PA、PB于D、E，若△PDE的周长为20cm，则PA长为 ．

32．如图，中，，它的周长为16．若与三边分别切于E，F，D点，则DF的长为

33．如图，若△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB＝5，BC＝13，CA＝12，则阴影部分的周长是 ．

34．如图，为的直径，、为上的点，连接、、、，为延长线上一点，连接，且，．若的半径为，则点到的距离为 ．

35．如图，PA，PB切⊙O于A，B两点，CD切⊙O于点E，分别交PA，PB于点C，D．若⊙O的半径为2，∠P＝60°，则△PCD的周长等于 ．


三、解答题
36．如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，点D为⊙O上一点，且CD＝CB、连接DO并延长交CB的延长线于点E．
（1）判断直线CD与⊙O的位置关系，并证明；
（2）若BE＝8，DE＝16，求⊙O的半径．

37．如图，AC是⊙O的直径，弦BD交AC于点E，点F为BD延长线上一点，∠DAF＝∠B．

(1)求证：AF是⊙O的切线；
(2)若⊙O的半径为5，AD是AEF的中线，且AD＝6，求AE的长．
38．如图，在△ABC中，已知∠ABC＝90o，在AB上取一点E，以BE为直径的⊙O恰与AC相切于点D，若AE＝2cm，AD＝4cm．
(1)求⊙O的直径BE的长；
(2)计算△ABC的面积．

39．已知，，分别与相切于，，三点，，．

（Ⅰ）如图1，求的长；
（Ⅱ）如图2，当，时，连接，，求，的长．
40．如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接OC，PB，已知PB=6，DB=8，∠EDB=∠EPB．

(1)求证：PB是⊙O的切线；
(2)求⊙O的半径；
(3)连接BE，求BE的长．
41．如图，PA、PB、CD是的切线，点A、B、E为切点．

(1)如果的周长为10，求PA的长；
(2)如果，
①求；
②连AE，BE，求．

参考答案：
1．A
【分析】由切线长定理可得，再分别设，，根据三角形的三边长度列出方程组求解未知数即可．
【详解】解：的周长为36．，，
∴,
由切线长定理可得，
，
设，，

解得：
∴；
故选：A．
【点睛】本题主要考查切线长定理：从圆外一点引圆的两条切线，它们的切线长相等；熟练掌握圆的切线长定理是解决本题的关键．
2．C
【分析】根据切线长定理即可得结论．
【详解】解：∵PA、PB切⊙O于点A、B，
∴PB=PA=20，
∵CD切⊙O于点E，交PA、PB于C、D两点，
∴CA=CE，DB=DE，
∴PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=20+20=40．
则△PCD的周长是40．
故选：C．
【点睛】本题考查了切线长定理，解决本题的关键是掌握切线的性质．
3．C
【分析】根据切线长定理得到PB=PA、CA=CE，DE=DB，根据三角形的周长公式计算即可．
【详解】解：∵PA、PB分别切⊙O于点A、B，
∴PB=PA=4，
∵CD切⊙O于点E且分别交PA、PB于点C，D，
∴CA=CE，DE=DB，
∴△PCD的周长=PC+PD+CD=PC+CA+PD+DB=PA+PB=8，
故选：C．
【点睛】本题考查的是切线长定理的应用，切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角．
4．C
【分析】先利用⊙O截△ABC的三条边所得的弦长相等，得出即O是△ABC的内心，从而，∠1=∠2，∠3=∠4，进一步求出∠BOC的度数．
【详解】解：如图，

∵△ABC中∠A=50°，⊙O截△ABC的三条边所得的弦长相等，
∴O到三角形三条边的距离相等，
即O是△ABC的内心，
∴∠1=∠2，∠3=∠4，
∠1+∠3=（180°-∠A）=（180°-50°）=65°，
∴∠BOC=180°-（∠1+∠3）
=180°-65°
=115°．
故选：C．
【点睛】本题考查的是三角形的内心，及三角形内角和定理，掌握三角形内心的性质是解答此题的关键．
5．C
【分析】连接IE、IF，根据切线的性质可得∠AEI＝∠AFI＝90°，从而得到∠A＝180°﹣∠EIF，再由圆周角定理可得∠EDF＝90°﹣∠A，即可求解．
【详解】解：连接IE、IF，如图，

∵内切圆I和边AC、AB分别相切于点E、F，
∴IE⊥AC，IF⊥AB，
∴∠AEI＝∠AFI＝90°，
∴∠A＝180°﹣∠EIF，
∵∠EDF＝∠EIF，
∴∠EDF＝90°﹣∠A，
∵∠B＝55°，∠C＝75°，
∴∠A＝180°﹣∠B﹣∠C＝180°﹣55°﹣75°＝50°，
∴∠EDF＝90°﹣×50°＝65°．
故选：C．
【点睛】本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线的性质．
6．C
【分析】利用垂径定理可对①②进行判断；利用圆周角定理可得到CM、AN为角平分线，则利用三角形内心的定义可对③进行判断；根据P是△ABC的内心得出∠APC=90°+∠B，进而得出∠MON+∠B=180°，再代入求解即可．
【详解】解：作BC的垂直平分线，则ON平分，则＝，所以①正确；
作AB的垂直平分线，则OM平分，则＝，2AM＞AB，所以②错误；
∵M点为的中点，∴∠ACM=∠BCM，
∵点N为的中点，∴∠BAN=∠CAN，
故P点为△ABC的内心，所以③正确；
∵∠APC=180°-∠PAC-∠PCA=180°-∠BAC-∠BCA=180°-(∠BAC+∠BCA)=180°-(180°-∠B)=90°+∠B，
∴2∠MPN=2∠APC=180°+∠B，
又OM⊥AB，ON⊥BC，∴∠MON+∠B=180°，
∴∠MON+2∠MPN=∠MON+180°+∠B=180°+180°=360°，故④正确，
∴正确的结论有3个，
故选：C．
【点睛】本题考查了垂径定理、圆周角定理、三角形内心及外心的性质、线段的垂直平分线的尺规作图等，熟练掌握各图形的性质及尺规作图步骤是解决本题的关键．
7．B
【分析】根据AB＝AC，∠BAC＝36°，可得∠ABC＝72°，由AE＝BE，∠ABE＝∠CBE＝36°，可得点F是三角形角平分线的交点，进而可以判断点F到△ABC三边的距离相等．
【详解】解：∵AB＝AC，∠BAC＝36°，
∴∠ABC＝∠ACB（180°﹣36°）＝72°，
∵AD⊥BC，AB＝AC，
∴AD是∠BAC的角平分线，
∵AE＝BE，
∴∠EAB＝∠EBA＝36°，
∴∠EBC＝72°﹣36°＝36°，
∴∠ABE＝∠CBE，
∴BE是∠ABC的角平分线，
∵BE、AD交于点F，
∴点F是三角形内角平分线的交点，
∴点F到△ABC三边的距离相等．
由已知条件均得不出A，C，D选项
故选：B．
【点睛】本题考查了三角形的内切圆与内心、等腰三角形的性质、三角形的外接圆与外心，解决本题的关键是区分三角形的内心与外心．
8．B
【分析】当时，直线是的切线．连接OA．结合题意可知，从而得出．再根据，即得出，从而即可求出，即证明直线是的切线．
【详解】解：当时，直线是的切线．
证明：如图，连接OA．
∵，
∴．
∵，
∴，
∴，即，
∴直线是的切线．
故选：B．

【点睛】本题考查切线的判定，三角形内角和定理，等腰三角形的判定和性质．连接常用的辅助线是解题关键．
9．C
【分析】首先过点O作直径AF，连接BF，根据同弧所对的圆周角相等可得∠C＝∠AFB，进而可得到∠BAE＝∠F，再根据直径所对的圆周角是90°，可证出∠AFB+∠BAF＝90°，再利用等量代换可得∠BAE+∠BAF＝90°，进而得到直线DE与⊙O相切．
【详解】解：当时，直线与相切．
理由如下：
作AF交圆O于F点，连接BF．
∵∠F，∠C是同弧AB所对的角，
∴∠C＝∠F，
∵∠BAE＝∠C，
∴∠BAE＝∠F，
∵AF为直径，
∴∠ABF＝90°，
∴在三角形ABF中，∠F+∠BAF＝90°，
∵∠F＝∠BAE，
∴∠BAE+∠BAF＝90°，
∴FA⊥DE，
∴直线DE与⊙O相切．
故选：C
．
【点睛】此题主要考查了切线的判定，关键是正确作出辅助线，证明∠BAE+∠BAF＝90°．
10．D
【分析】分别利用切线的判定进而得出∠BAT=90°，得出答案即可．
【详解】A．
∵AB=4，AT=3，BT=5，∴AB2+AT2=BT2，∴△BAT是直角三角形，∴∠BAT=90°，∴直线AT是⊙O的切线，故此选项错误；
B．∵∠B=45°，AB=AT，∴∠T=45°，∴∠BAT=90°，∴直线AT是⊙O的切线，故此选项错误；
C．∵AB为直径，∴∠BAC=90°．
∵∠B=55°，∴∠BAC=35°．
∵∠TAC=55°，∴∠CAT=90°，∴直线AT是⊙O的切线，故此选项错误；
D．∠ATC=∠B，无法得出直线AT是⊙O的切线，故此选项正确．
故选D．

【点睛】本题考查了切线的判定，正确把握判定方法得出∠BAT=90°是解题的关键．
11．A
【分析】根据AB=AC，连接AD，利用圆周角定理以及等腰三角形的性质可以得到点D是BC的中点，OD是△ABC的中位线，OD∥AC，然后由DE⊥AC，得到∠ODE=90°，可以证明DE是⊙O的切线，可判断B选项正确；
若DE是⊙O的切线，同上法倒推可证明AB=AC，可判断D选项正确；
根据CD=BD，AO=BO，得到OD是△ABC的中位线，同上可以证明DE是⊙O的切线，可判断C选项正确；
若，没有理由可证明DE是⊙O的切线．
【详解】解：当AB=AC时，如图：连接AD，

∵AB是⊙O的直径，
∴AD⊥BC，
∴CD=BD，
∵AO=BO，
∴OD是△ABC的中位线，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∴DE是⊙O的切线，所以B选项正确；
当DE是⊙O的切线时，如图：连接AD，

∵DE是⊙O的切线，
∴DE⊥OD，
∵DE⊥AC，
∴OD∥AC，
∴OD是△ABC的中位线，
∴CD∥BD，
∵AB是⊙O的直径，
∴AD⊥BC，
∴AD是线段BC的垂直平分线，
∴AB=AC，所以D选项正确；
当CD=BD时，又AO=BO，
∴OD是△ABC的中位线，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∴DE是⊙O的切线，所以C选项正确．
若，没有理由证明DE是⊙O的切线，所以A选项错误．
故选：A．
【点睛】本题考查了切线的判定和性质，正确的识别图形是解题的关键．
12．C
【分析】先利用切线长定理得到PA=PB，再利用∠APB=60°可判断△APB为等边三角形，然后根据等边三角形的性质求解．
【详解】解：∵PA，PB为⊙O的切线，
∴PA=PB，
∵∠APB=60°，
∴△APB为等边三角形，
∴AB=PA=5．
故选：C．
【点睛】本题考查了切线长定理以及等边三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．
13．B
【分析】根据切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.
【详解】A、与圆只有一个交点的直线是圆的切线,故本选项错误;
B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;
C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;
D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.
故选B.
【点睛】本题考查了切线的判定方法，如果直线与圆只有一个公共点，这时直线与圆的位置关系叫做相切，这条直线叫做圆的切线，这个公共点叫做切点；经过半径外端点并且垂直于这条半径的直线是圆的切线.
14．C
【分析】根据圆周角定理推论可求∠CAD=32°，再根据三角形内心的定义可求∠BAC，再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB，再根据三角形内角和定理可求∠BEC的度数．
【详解】在⊙O中，
∵∠CBD=32°，
∵∠CAD=32°，
∵点E是△ABC的内心，
∴∠BAC=64°，
∴∠EBC+∠ECB=（180°-64°）÷2=58°，
∴∠BEC=180°-58°=122°．
故选：C．
【点睛】考查了三角形的内切圆与内心，圆周角定理推论，三角形内角和定理，关键是得到∠EBC+∠ECB的度数．
15．B
【分析】根据轴对称图形和中心对称图形的定义判断①，根据圆的基本性质判断②③，根据三角形内接圆和外切圆的定义判定④⑤即可．
【详解】解：①平⾏四边形是中⼼对称图形，也是轴对称图形，错误，平行四边形是中心对称图形，不是轴对称图形；②直径是最长的弦，正确，半径是最短的弦，错误，半径不是弦；③过切点的直线是圆的切线，错误；④三角形的外⼼是三条边垂直平分线的交点，正确；⑤三角形的内⼼是三条内角平分线的交点，正确．
故选：B．
【点睛】题目主要考查命题与定理的知识，解题的关键是理解中心对称图形和轴对称图形的性质、圆的基本性质及三角形内接圆外切圆的性质．
16．C
【分析】根据切线长定理，可以得到等量关系，AE=AF，BE=BH，DF=DG，CG=CH，又根据题目中已知AD=3，BC=6，从而进行等量替换计算出AB+CD的长度．
【详解】解：∵AB、BC、CD、DA都是的切线，
∴可以假设切点分别为E、H、G、F，如图所示：
∴AE=AF，BE=BH，DF=DG，CG=CH，
∴AB+CD=AE+BE+DG+CG=AF+BH+DF+CH=AD+BC
∵AD=3，BC=6
∴AB+CD=3+6=9
故选C．
．
【点睛】本题主要考查了切线长定理，可以证明圆的外切四边形的对边和相等，即可解决问题．
17．D
【分析】设内切圆的半径为r，根据公式：，列出方程即可求出该三角形内切圆的半径．
【详解】解：设内切圆的半径为r

解得：r=1
故选D．
【点睛】此题考查的是根据三角形的周长和面积，求内切圆的半径，掌握公式：是解决此题的关键．
18．D
【分析】根据弧、弦、圆心角的关系，垂径定理，切线的判定定理，三点确定一个圆判断即可．
【详解】解：①在同圆或等圆中，相等的圆心角所对的弧相等；故错误；
②平分弦（不是直径）的直径垂直于弦；故错误；
③垂直于半径且过半径的外端点的直线是圆的切线；故错误；
④E、F是∠AOB（∠AOB≠180°）的两边OA、OB上的两点，则E、O、F三点确定一个圆；故错误；
故选：D．
【点睛】本题考查了切线的判定定理，三点确定一个圆，垂径定理等知识，熟练掌握各性质和判定定理是解题的关键．
19．A
【分析】先运用圆的切线长定理可以得到：PA=PB，再利用等腰三角形的性质即可求出∠PAB的度数，最后利用切线的性质解题即可．
【详解】解：PA，PB是⊙O的切线，
，
，
，
，
，
，
．
故选：A．
【点睛】本题考查圆的切线长定理以及切线的性质，掌握切线长定理以及切线的性质是解题关键．
20．D
【分析】利用切线长定理、等腰三角形的性质、切割线定理即可得出．
【详解】、是的切线，切点是、，
，，
选项A、B错误；
，，
，
选项C错误；
根据已知不能得出是的中点，
故选项D正确；
故选D．
【点睛】本题考查了切线长定理、等腰三角形的性质，解题的关键是熟练掌握切线长定理，属于基础题．
21．D
【分析】设光盘的圆心为,直角三角板与的切点为，连接，根据切线长定理可得，进而利用勾股定理以及含30度角的直角三角形的性质，求得的长，即可求得答案．
【详解】如图，设光盘的圆心为,直角三角板与的切点为，连接，

是的切线，
，，



此光盘的直径为
故选D
【点睛】本题考查了切线长定理，勾股定理，含30度角的直角三角形的性质，掌握切线长定理是解题的关键．
22．C
【分析】根据题意判断AD是∠BAC的角平分线，然后逐个选项判断即可．
【详解】根据作图步骤得：AD是∠BAC的角平分线
A、在△ABD中，AD+BD＞AB，故选项A错误，不符合题意；
B、由角平分线得，而不一定成立，选项B错误，不符合题意；
C、△ABC的内心是三条角平分线的交点，故选项C正确，符合题意；
D、△ABC的外心是三边中垂线的交点，故选项D错误，不符合题意；
故选：C．
【点睛】本题考查尺规作图、三角形内心与外心的定义和三角形三边的关系，熟练掌握这些定义是解题的关键．
23．C
【分析】中，点为的内心，可求出CAI的度数，根据四边形AIDC的内角和即可得出结论．
【详解】解：在中，，
BAC＝180－42－58＝80
点为的内心，
CAI＝BAI＝＝40
四边形AIDC的内角和180（4－2）＝360，且
＝360－－－CAI＝360－90－40－58＝172
故选C．
【点睛】本题考查了三角形内心的定义及多边形的内角和，牢固掌握相关概念是解题的关键．
24．B
【分析】连接OC，证明△PAO≌△PCO（SAS），得到∠OCP=90°，进而求得．
【详解】
如图，连接OC，
因为OB=OC，
所以∠OCB=∠OBC=70°，
所以∠BOC=180°-70°-70°=40°，
又因为，
所以∠AOP=∠B=70°，
∴∠POC=180°-∠AOP-∠BOC=70°，
所以在△PAO和△PCO中，
，
所以△PAO≌△PCO（SAS），
所以∠OCP=∠OAP
因为PA与相切于点A，
所以∠OCP=∠OAP=90°，
所以∠OPC=180°-∠POC-∠OCP=20°，
故选：B．
【点睛】本题考查了圆的切线、证明全等三角形和平行线等知识内容，灵活运用条件，学会选择辅助线是解题的关键．
25．A
【分析】连接，设，的半径为，由勾股定理求出，在中，由可得方程，代入的值，可求出x的值，再根据勾股定理可得出结论．
【详解】解：连接，如图所示，

∵PC，PD是的切线，
∴
设
∵
∴
∴
设的半径为
∴
在中，，
解得，
在中，
∵是的切线，
∴
在中，
∵
∵
∴
整理得，
∴
解得，或（舍去）
∴
∴

在中，，故A正确．
故选：A．
【点睛】本题主要考查了切线长定理，垂径定理，勾股定理等知识，正确作出辅助线是解答本题的关键．
26．C
【分析】如图，过点D分别作DE⊥AB于E，DF ⊥BC于F， DH⊥AC于H， 连接AD， CD，求出AB的长，根据内心的性质，求出BE的长，再根据S△ABC = S△ABD + S△BDC + S△ADC，求出DE的长，由勾股定理即可得答案．
【详解】解： 如下图，过点D分别作DE⊥AB于E，DF ⊥BC于F， DH⊥AC于H， 连接AD， CD，

∵BC是⊙O的直径，
∴∠BAC= 90°，
∵BC＝5，AC＝3，
∴ ，
∵点D是△ABC的内心，
∴ DE= DF= DH，AE= АН，BE= BF，CF= CH，
设BE= x，则BF= x，AE=4- x，CF=5-x，CH=5-x，AН=4-x，
∵AC=3，
∴4-x+5-x=3，
解得：x=3
∴BE=3，
设DE= r，
∵S△ABC = S△ABD + S△BDC + S△ADC，
∴ ，
解得：r= 1，
∴ DE= 1，
在Rt△BDE中， ，
故选：C．
【点睛】本题考查了圆的有关性质，内心的性质，勾股定理的应用，解题的关键是作垂线，构造直角．
27．C
【分析】由切线长定理可求得PA=PB，AC=CE，BD=ED，则可求得答案．
【详解】解：∵PA、PB分别切⊙O于点A、B，CD切⊙O于点E，
∴PA=PB=6，AC=EC，BD=ED，
∴PC+CD+PD=PC+CE+DE+PD=PA+AC+PD+BD=PA+PB=8+8=16，
即△PCD的周长为16．
故选：C．
【点睛】本题主要考查切线的性质，利用切线长定理求得PA=PB、AC=CE和BD=ED是解题的关键．
28．D
【分析】连接连接，，并延长交于点，根据是等边的内切圆，求出，求出，根据勾股定理求出，同理求出，得到，求出，即可得出答案．
【详解】解：连接，，并延长交于点，

是等边的内切圆，
，，
，
由勾股定理得：，
同理，
，
是等边三角形，，，三点共线，
，
．
故选：D．
【点睛】本题考查了等边三角形性质，三角形的内切圆，勾股定理，含角的直角三角形性质等知识点的应用，关键是构造直角三角形，并求出和的长．
29．D
【分析】根据圆周角定理和AB=AC可得结论①；根据等边对等角和平行线的性质可得∠ABC＝∠ACB＝∠DCE＝∠DEC，可得结论②；无法确定∠BAC=90°，③不一定正确；由DB＝DC＝DE可得点E在以BC为直径的圆上，于是∠BEC＝90°，由AB∥CE即可得结论④；
【详解】解：∵AB为直径，
∴∠ADB＝90°，
∴AD⊥BC，
而AB＝CA，
∴BD＝DC，所以①正确；
∵AB＝CA，
∴∠ABC＝∠ACB，
而CD＝ED，
∴∠DCE＝∠DEC，
∵CF∥AB，
∴∠ABC＝∠DCE，
∴∠ABC＝∠ACB＝∠DCE＝∠DEC，
∴△CBA∽△CED，所以②正确；
∵△ABC不能确定为直角三角形，
∴∠ABC不能确定等于45°，
∴与不能确定相等，所以③不一定正确；
∵DB＝DC＝DE，
∴点E在以BC为直径的圆上，
∴∠BEC＝90°，
∴CE⊥BE，
而CF∥AB，
∴AB⊥BE，
∴BE为⊙O的切线，所以④正确；
综上所述①②④正确，
故选： D．
【点睛】本题考查了圆周角定理，等腰三角形的性质，相似三角形的判定，切线的判定等知识；掌握相关性质和判定方法是解题关键．
30．50°
【分析】根据切线长定理得到∠BPO＝∠APO，结合图形计算，得到答案．
【详解】解：∵PA、PB是⊙O的切线，
∴∠BPO＝∠APO＝25°，
∴∠BPA＝50°，
故答案为：50°．
【点睛】本题考查了切线长定理，熟知切线长定理的性质是解题的关键．
31．10cm
【分析】根据切线长定理，可将△PDE的周长转化为两条切线长的和，已知了△PDE的周长，即可求出切线的长．
【详解】解：根据切线长定理得：
AD＝CD，CE＝BE，PA＝PB，
则△PDE的周长＝
2PA＝20，
PA＝10．
故答案为：
【点睛】本题考查的是切线长定理，三角形的周长的计算，掌握切线长定理是解题的关键
32．2
【分析】根据切线长定理求出AD=AF，BE=BD，CE=CF，得出等边三角形ADF，推出，根据BC=6，求出BD+CF=6，求出AD+AF=4，即可求出答案．
【详解】解：∵⊙O与BC，AC，AB三边分别切于E，F，D点，
∴AD=AF，BE=BD，CE=CF，
∵BC=BE+CE=6，
∴BD+CF=6，
∵AD=AF，∠A=60°，
∴△ADF是等边三角形，
∴AD=AF=DF，
∵AB+AC+BC=16，BC=6，
∴AB+AC=10，
∵BD+CF=6，
∴AD+AF=4，
∵AD=AF=DF，
∴DF=AF=AD=，
故答案为：2．
【点睛】本题考查了对切线长定理的应用，解题的关键是求出AD+AF的值．
33．8
【分析】利用勾股定理的逆定理证明△ABC为直角三角形，∠A＝90°，根据切线的性质，可得四边形OFAE为正方形，设OE＝r，继而根据切线长定理求得，根据正方形的性质即可求解．
【详解】∵AB＝5，BC＝13，CA＝12，
∴，
∴△ABC为直角三角形，∠A＝90°，
∵AB、AC与⊙O分别相切于点E、F，
∴OF⊥AB，OE⊥AC，
∴四边形OFAE为矩形，
∵OE=OF
∴四边形OFAE为正方形，
设OE＝r，
则AE＝AF＝r，
∵△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，
∴BD＝BF＝5﹣r，CD＝CE＝12﹣r，
∴5﹣r+12﹣r＝13，
∴r＝2，
∴阴影部分（即四边形AEOF）的面积是2×4＝8．
故阴影部分的周长是：8．
【点睛】本题考查了三角形内切圆的性质，切线长定理，勾股定理的逆定理，正方形的性质，综合运用以上知识是解题的关键．
34．/
【分析】连接OC，证明CD⊥OC；运用勾股定理求出OD=10，过点A作AF⊥DC，交DC延长线于点F，过点C作CG⊥AD于点G，在Rt△OCD中运用等积关系求出CD，同理，在△ACD中运用等积关系可求出AF
【详解】解：连接OC，

∵AB是圆的直径，
∴
∴
∵
∴
∵
∴
∴
∴，即OC⊥CD
∵的半径为
∴

在Rt△OCD中，
∴
∴
过点A作AF⊥DC，交DC延长线于点F，过点C作CG⊥AD于点G，
∵
∴，解得，
同理：
∴
∴
故答案为：
【点睛】本题考查了切线的判定、三角形面积、勾股定理等知识，解题的关键是作辅助线，构造直角三角形．
35．
【分析】连接OA，OB，OP，根据切线的性质以及角平分线的判定得出PO是∠APB的角平分线，利用勾股定理求出PA的长，再根据切线长定理得出AC＝CE，BD＝DE，即可求解．
【详解】解：如图，连接OA，OB，OP，

∵PA，PB切⊙O于A，B两点，OA，OB是半径，
∴OA⊥PA，OB⊥PB，且OA＝OB，
∴PO是∠APB的平分线，
∵∠APB＝60°，
∴∠APO＝30°，
∴OP＝2OA＝4，
在Rt△APO中，由勾股定理得AP＝，
∵PA，PB切⊙O于A，B两点，
∴PA＝PB＝，
∵CD切⊙O于点E，
∴AC＝CE，BD＝DE，
∴△PCD的周长＝PC+PD+CD＝PC+CA+PD+DB＝PA+PB＝，
故答案为：．
【点睛】本题考查了切线的性质，角平分线的判定，勾股定理，切线长定理等知识，熟练掌握切线的性质以及角平分线的判定是解题的关键．
36．（1）相切，理由见解析；（2）⊙O的半径为6
【分析】（1）欲证明CD是切线，只要证明OD⊥CD，利用全等三角形的性质即可证明；
（2）设⊙O的半径为r，在Rt△OBE中，根据OE2＝EB2+OB2，可得（16﹣r）2＝r2+82，推出r＝6，即可解决问题．
【详解】解：（1）相切，理由如下，
如图，连接OC，
在△OCB与△OCD中，
，
∴△OCB≌△OCD（SSS），
∴∠ODC＝∠OBC＝90°，
∴OD⊥DC，
∴DC是⊙O的切线；
（2）设⊙O的半径为r，
在Rt△OBE中，∵OE2＝EB2+OB2，
∴（16﹣r）2＝r2+82，
∴r＝6，
∴⊙O的半径为6．

【点睛】本题考查了圆的切线的判定、全等三角形的判定和性质、勾股定理等知识，正确添加辅助线，熟练掌握和灵活应用相关知识解决问题是关键．
37．(1)见解析
(2)

【分析】（1）由圆周角定理得∠ADC=90°，则∠ACD+∠DAC=90°，从而说明，即可证明结论；
（2）作于点H，利用△ADH～△ACD，，求出AH的长，再利用直角三角形斜边上中线的性质得出AD=DE，利用等腰三角形的性质可得答案．
【详解】（1）证明：∵AC是直径，
∴∠ADC=90°，
∴∠ACD+∠DAC=90°，
∵∠ACD=∠B，∠B=∠DAF，
∴∠DAF=∠ACD，
∴∠DAF+∠DAC=90°，
∴，
∵AC是直径，
∴AF是⊙O的切线；
（2）解：作于点H，

∵⊙O的半径为5，
∴AC=10，
∵∠AHD=∠ADC=90°，∠DAH=∠CAD，
∴△ADH～△ACD，
∴，
∴，
∵AD＝6，
∴，
∵AD是△AEF的中线，∠EAF=90°，
∴AD=ED，
．
【点睛】本题主要考查了圆周角定理，切线的判定定理，相似三角形的判定与性质，等腰三角形的性质等知识，根据相似三角形的判定与性质求出AH的长是解题的关键．
38．（1）BE＝6；(2) S△ABC＝24..
【分析】（1）连接OD，由切线的性质得OD⊥AC，，在Rt△ODA中运用勾股定理可以求出半径OD，即可求得直径BE的长；
（2）由切线长定理知，CD=BC，在Rt△ABC中运用勾股定理可以求出BC，则可由直角三角形的面积公式求得△ABC的面积．
【详解】（1）连接OD，

∴OD⊥AC
∴△ODA是直角三角形
设半径为r
∴AO＝r＋2
∴
解之得：r＝3
∴BE＝6
(2)∵∠ABC＝900
∴OB⊥BC
∴BC是⊙O的切线
∵CD切⊙O于D
∴CB＝CD
令CB＝x
∴AC＝x＋4， CB＝x，AB＝8
∵
∴x＝6.
∴S△ABC＝24（cm2）.
故答案为（1）BE＝6；(2) S△ABC＝24..

【点睛】本题考查勾股定理，切线的定义，切线长定理.
39．（Ⅰ）4；（Ⅱ），．
【分析】（Ⅰ）由切线长定理可知BM=BA=1，CM=CD=3，则BC=BM+CM=4；
（Ⅱ）如图所示，连接OD，OM，OA，先证明Rt△OCD≌Rt△OCM得到∠OCD=∠OCM，
同理可得∠OBA=∠OBM，即可求出∠OCM=30°，∠OBM=60°，OC=2OM，，由此即可求解．
【详解】解：（Ⅰ）∵AB，BC，CD都是圆O的切线，
∴BM=BA=1，CM=CD=3，
∴BC=BM+CM=4；
（Ⅱ）如图所示，连接OD，OM，OA，
∵BC，DC都是圆O的切线，
∴∠ODC=∠OMC=∠OMB=90°，CM=CD，
又∵OC=OC，
∴Rt△OCD≌Rt△OCM（HL），
∴∠OCD=∠OCM，
同理可得∠OBA=∠OBM，
∵∠DCB=60°，AB∥CD，
∴∠OCM=30°，∠ABM=120°
∴OC=2OM，∠OBM=60°，
∴，
∴，
∴．

【点睛】本题主要考查了切线长定理，切线的性质，平行线的性质，全等三角形的性质与判定，含30度角的直角三角形的性质，勾股定理，解题的关键在于能够熟练掌握切线长定理和切线的性质．
40．(1)见解析
(2)3
(3)

【分析】（1）由已知角相等及直角三角形的性质得到为直角，即可得证；
（2）在直角三角形中，由与的长，利用勾股定理求出的长，由切线长定理得到，由求出的长，在直角三角形中，设，则有，利用勾股定理列出关于的方程，求出方程的解得到的值，即为圆的半径．
（3）延长、相交于点，证明，由全等三角形的性质得出，，求出的长，则可得出答案．
【详解】（1）证明：，
，
，，，
，
，
为的切线；
（2）解：在中，，，
根据勾股定理得：，
与都为的切线，
，
；
在中，设，则有，
根据勾股定理得：，
解得：，
则圆的半径为3．
（3）延长、相交于点，

与都为的切线，
平分，
，
，
，
又，
，
，，
，
在中，，
．
【点睛】本题考查圆和三角形的综合应用．本题是中考题常考题型，熟练掌握圆中的等量关系，切线的证明方法，以及通过等量关系的转化证明三角形全等，利用解直角三角形解决求线段长度的问题是解题的关键．
41．(1)5
(2)①70°；②110°

【分析】（1）根据切线长定理求解即可；
（2）①根据三角形外角的性质得，再根据切线长定理得，最后由三角形内角和定理可得；
②连接OA，OB，由切线的性质和四边形内角和定理以及圆周角定理可得结论．
【详解】（1）∵分别切于点
∴
∴△的周长





∴
（2）①


∵分别切于点





②连接OA，OB

∵PA，PB是切线,
∴
∵
∴
∴
【点睛】本题主要考查了切线的性质，圆周角定理以及切线长定理等知识，熟练掌握相关性质是解答本题的关键．