初中数学1 探索勾股定理一等奖教学设计

导入新课

教师提出问题：

1.勾股定理的内容是什么？（请一名学生回答）

2.上节课我们仅仅是通过测量和数格子，对具体的直角三角形探索发现了勾股定理，对一般的直角三角形，勾股定理是否成立呢？这需要进一步验证，如何验证勾股定理呢？事实上，现在已经有几百种勾股定理的验证方法，这节课我们也将去验证勾股定理.

学生思考并积极回答

回顾上节课的探索过程，强调仍需对一般的直角三角形进行验证，培养学生严谨的科学态度；介绍世界上有数百种验证方法，激发学生兴趣.

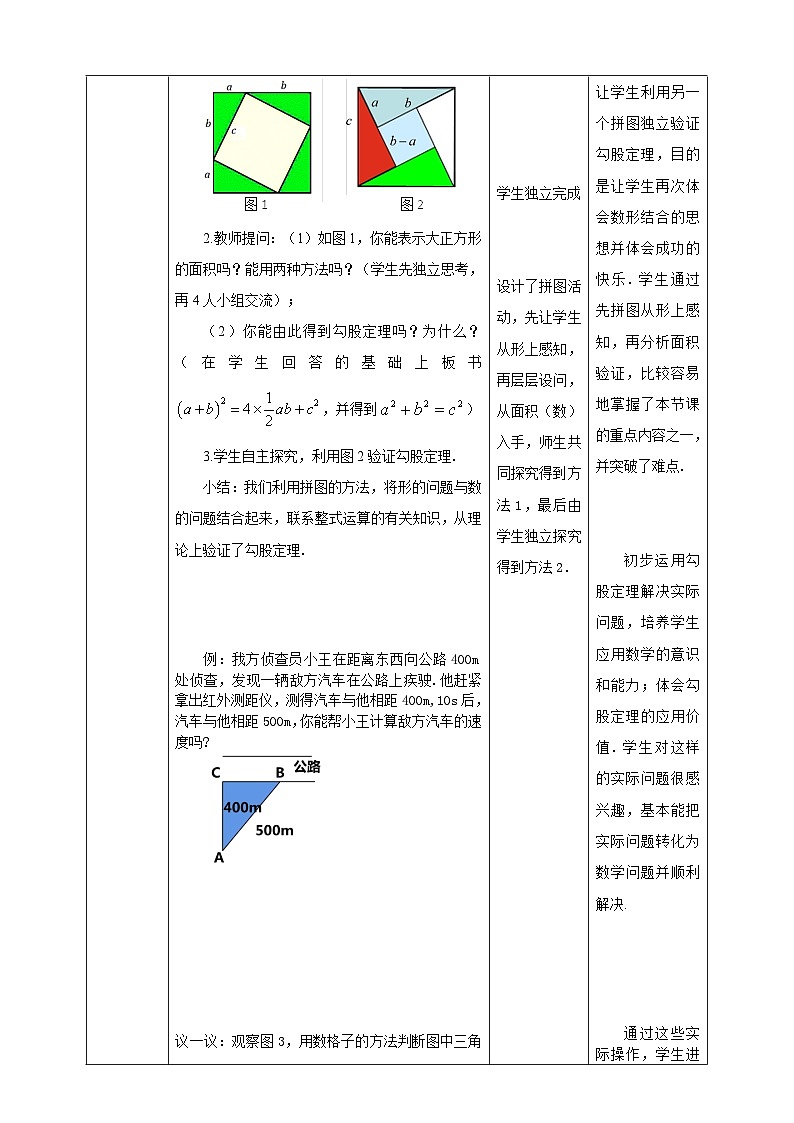
讲授新课

师：今天我们将研究利用拼图的方法验证勾股定理，请你利用自己准备的四个全等的直角三角形，拼出一个以斜边为边长的正方形.（请每位同学用2分钟时间独立拼图，然后再4人小组讨论.）

1.学生通过自主探究，小组讨论得到如图1、图2的两个图形.

2.教师提问：（1）如图1，你能表示大正方形的面积吗？能用两种方法吗？（学生先独立思考，再4人小组交流）；

（2）你能由此得到勾股定理吗？为什么？（在学生回答的基础上板书，并得到）

3.学生自主探究，利用图2验证勾股定理.

小结：我们利用拼图的方法，将形的问题与数的问题结合起来，联系整式运算的有关知识，从理论上验证了勾股定理.

例：我方侦查员小王在距离东西向公路400m处侦查，发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪，测得汽车与他相距400m,10s后，汽车与他相距500m，你能帮小王计算敌方汽车的速度吗?

议一议：观察图3，用数格子的方法判断图中三角形的三边长是否满足

学生通过自主探究，小组讨论得到方法。

学生独立完成

设计了拼图活动，先让学生从形上感知，再层层设问，从面积（数）入手，师生共同探究得到方法1，最后由学生独立探究得到方法2．

学生在教师的层层设问的引导下完成对勾股定理的验证，完成本节课的一个重点内容.然后让学生利用另一个拼图独立验证勾股定理，目的是让学生再次体会数形结合的思想并体会成功的快乐.学生通过先拼图从形上感知，再分析面积验证，比较容易地掌握了本节课的重点内容之一，并突破了难点.

初步运用勾股定理解决实际问题，培养学生应用数学的意识和能力；体会勾股定理的应用价值.学生对这样的实际问题很感兴趣，基本能把实际问题转化为数学问题并顺利解决.

通过这些实际操作，学生进行一步加深对数形结合的理解，拼图也会产生感性认识，也为论证勾股定理做好准备。

利用分组讨论，加强合作意识。

课堂练习

1.用四个边长均为a，b，c的直角三角板，拼成如图所示的图形，则下列结论中正确的是(　　)

 A．c2=a2+b2                 B．c2=a2+2ab+b2

C．c2=a2-2ab+b2              D．c2=(a+b)2

2．如图，一个长为2.5 m的梯子，一端放在离墙脚1.5 m处，另一端靠墙，则梯子顶端距离墙脚(　　)

 A．0.2 m    B．0.4 m     C．2 m     D．4 m

3.如图，王大爷准备建一个蔬菜大棚，棚宽8m，高6m，长20m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，阳光透过的最大面积是_________.

4．如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙脚的距离为0.7 m，顶端距离地面2.4 m．如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2 m，则小巷的宽度为                                 。

5．两棵树之间的距离为8 m，两棵树的高度分别是8 m，2 m，一只小鸟从一棵树的树顶飞到另一棵树的树顶，这只小鸟至少要飞多少米？

学生利用所学知识做练习。

从简单的问题入手，运用勾股定理解决问题，让学生在解题过程中掌握勾股定理的应用,达到“学数学，用数学”的目的，进一步培养学生解决问题的能力和推理论证的能力

课堂小结

通过本节课的学习，你们有什么收获？

学生归纳本节所学内容，并体验核心素养的形成。

通过小结让学生理清本节课的知识结构，感受探究过程中乐趣，体验克服困难的过程，树立学习数学的信心。

板书

1.1．2探索勾股定理

复习勾股定理:  

勾股定理：直角三角形两直角边的平方和等于斜边的平方．如果用，，分别表示直角三角形的两直角边和斜边，那么．