初中数学北师大版八年级上册第一章 勾股定理1 探索勾股定理优质课课件ppt

这是一份初中数学北师大版八年级上册第一章 勾股定理1 探索勾股定理优质课课件ppt，共19页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

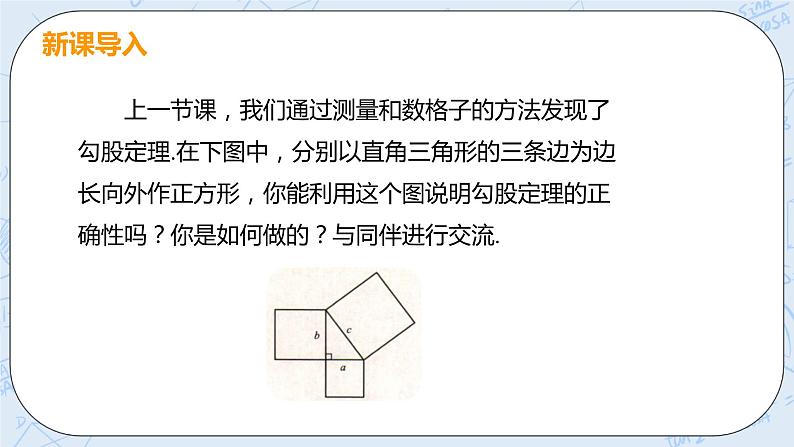
上一节课，我们通过测量和数格子的方法发现了勾股定理.在下图中，分别以直角三角形的三条边为边长向外作正方形，你能利用这个图说明勾股定理的正确性吗？你是如何做的？与同伴进行交流.
知识点1 勾股定理的验证
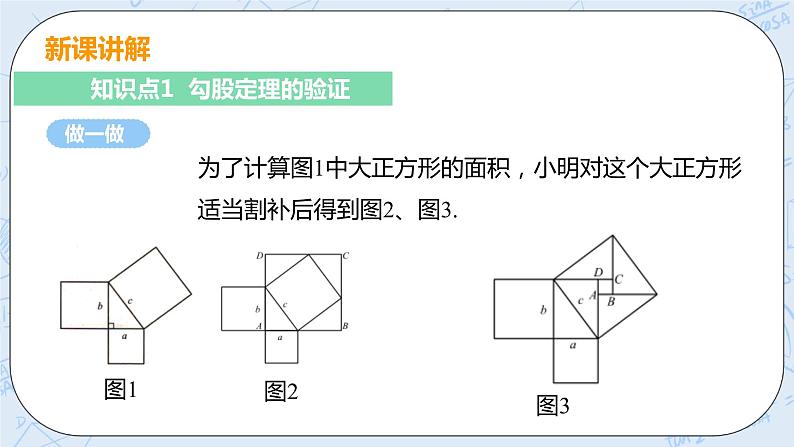
为了计算图1中大正方形的面积，小明对这个大正方形适当割补后得到图2、图3.
1.将所有三角形和正方形的面积用a,b,c的关系式表示出来； 2.图2、图3中正方形ABCD的面积分别是多少？你们有哪 些表示方式？与同伴进行交流. 3.你能分别利用图2、图3验证勾股定理吗？
常用方法：通过拼图法利用求面积来验证．这种 方法是以数形转换为指导思想，图形拼补为手段， 以各部分面积之间的关系为依据而达到目的的．
2．用拼图法验证勾股定理的思路： (1)图形经过割补、拼接后，只要没有重叠，没有空 隙，面积不会改变；(2)根据同一种图形的面积的不同表示方法列出等式；(3)利用等式性质验证结论成立，即拼出图形→写出 图形面积的表达式→找出等量关系→恒等变形→ 推导结论．
如图是用硬纸板做成的四个两直角边长分别是a，b，斜边长为c的全等的直角三角形和一个边长为c的正方形，请你将它们拼成一个能说明勾股定理正确性的图形． (1)画出拼成的这个图形的示意图； (2)说明勾股定理的正确性． 
分析：可以以边长为c的正方形为基础，一在形外补拼(不 重叠)成新的正方形；二在形内叠合成新的正方形．
解：方法一(补拼法)：(1)如图. (2)因为大正方形的面积可以表示为(a＋b)2， 也可以表示为c2＋4× ab， 所以(a＋b)2＝c2＋4× ab， a2＋b2＋2ab＝c2＋2ab.
所以a2＋b2＝c2， 即直角三角形两直角边的平方和 等于斜边的平方．方法二(叠合法)：(1)如图.(2)因为大正方形的面积可以表示为c2， 也可以表示为 ab×4＋(b－a)2， 所以c2＝ ab×4＋(b－a)2，c2＝2ab＋b2－2ab＋a2. 所以a2＋b2＝c2， 即直角三角形两直角边的平方和等于斜边的平方．
知识点2 勾股定理的应用
勾股定理的应用：（1）已知直角三角形的两边长，求其第三边长（2）已知直角三角形的一边，确定其另两边长之间的关系（3）证明含有平方关系的几何关系（4）解决生产、生活中的实际问题
我方侦察员小王在距离东西向公路400m处侦察，发现一辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪，测得汽车与他相距400m，10s后，汽车与他相距500m,你能帮小王计算敌方汽车的速度吗？
分析：根据题意，可以画出右图，其中点A表示小王所在位置，点C、点B表示两个时刻敌方汽车的位置.
由于小王距离公路400m，因此∠C是直角，这样就可以由勾 股定理来解决这个问题了.
解：由勾股定理，可以得到AB2=BC2+AC2， 也就是5002=BC2+4002, 所以BC=300.敌方汽车10s行驶了300m， 那么它1h行驶的距离为300×6×60=108000（m）, 即它行驶的速度为108km/h.
1.用四个边长均为a，b，c的直角三角板，拼成如 图所示的图形，则下列结论中正确的是(　　) A．c2＝a2＋b2 B．c2＝a2＋2ab＋b2 C．c2＝a2－2ab＋b2 D．c2＝(a＋b)2
2.两棵树之间的距离为8 m，两棵树的高度分别是8 m，2 m，一只小鸟从一棵树的树顶飞到另一棵树的树顶，这只小鸟至少要飞多少米？
分析：先根据题意画出图形，然后添加辅助线，构造直角三角形，再利用勾股定理求解．
解：根据题意画出示意图，如图所示， 两棵树的高度分别为AB＝8 m，CD＝2 m， 两棵树之间的距离BD＝8 m， 过点C作CE⊥AB，垂足为E，连接AC. 则BE＝CD＝2 m，EC＝BD＝8 m， AE＝AB－BE＝8－2＝6(m)． 在Rt△ACE中，由勾股定理，得AC2＝AE2＋EC2， 即AC2＝62＋82＝100，所以AC＝10 m. 答：这只小鸟至少要飞10 m．