




数学八年级上册1 探索勾股定理教学ppt课件
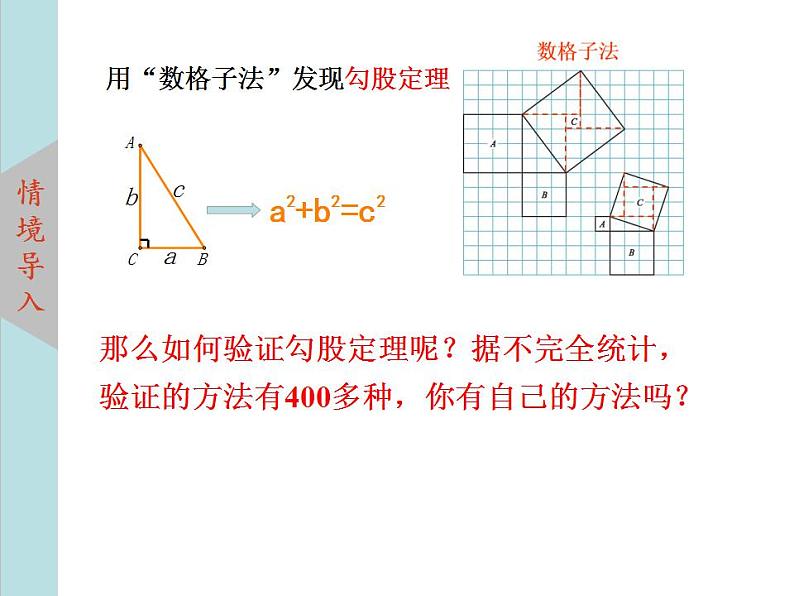
展开那么如何验证勾股定理呢?据不完全统计,验证的方法有400多种,你有自己的方法吗?
用“数格子法”发现勾股定理
1.1 探索勾股定理 第2课时 验证勾股定理与应用
1. 学会用几种方法验证勾股定理.2. 能够运用勾股定理解决简单实际问题.
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
大正方形的面积可以表示为 ;也可以表示为 .
∵ (a+b)2 = c2 + 4• ab
a2+2ab+b2 = c2 +2ab
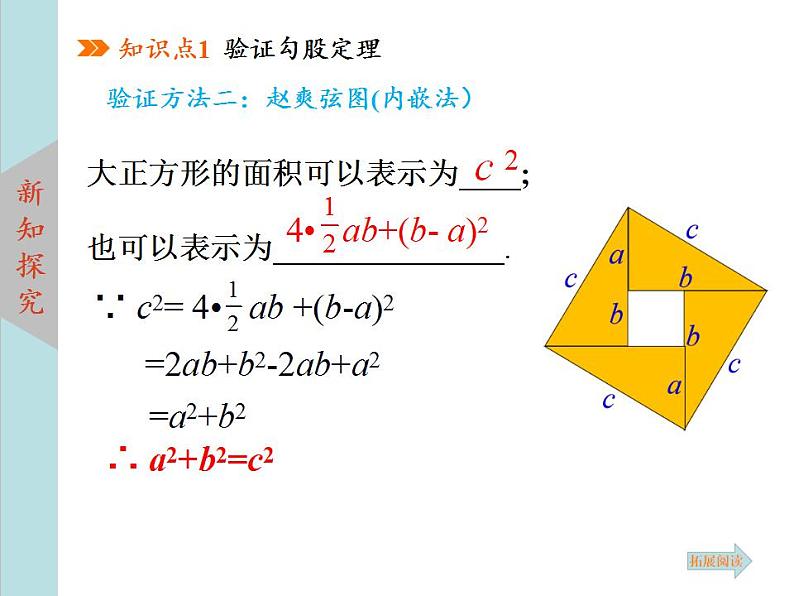
∴ a2+b2=c2
验证方法一:毕达哥拉斯证法(外镶法)
验证方法二:赵爽弦图(内嵌法)
大正方形的面积可以表示为 ;也可以表示为 .
4• ab+(b- a)2
∵ c2= 4• ab +(b-a)2
=2ab+b2-2ab+a2
梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得 ,化简,得
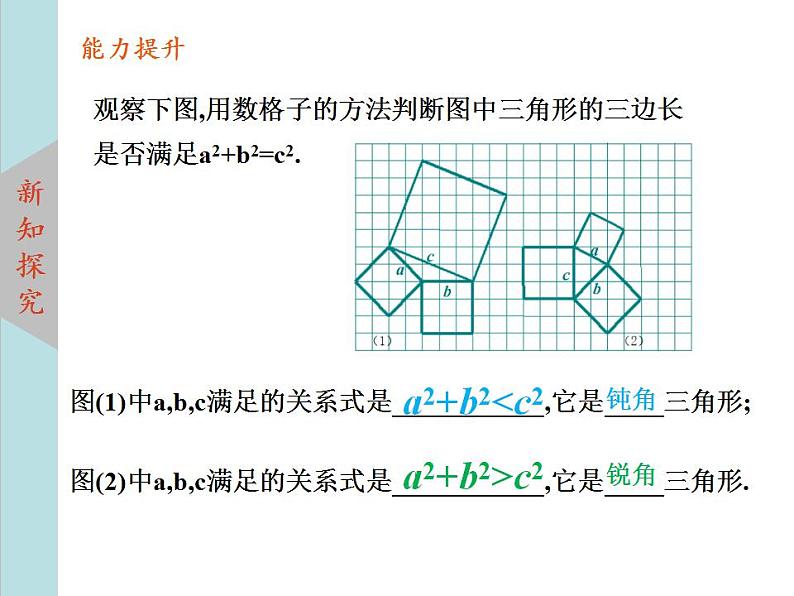
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.
图(1)中a,b,c满足的关系式是 ,它是 三角形;图(2)中a,b,c满足的关系式是 ,它是 三角形.
例1. 我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
勾股定理的实际应用--航向问题
解:由勾股定理,得BC2=AB2-AC2=5002-4002,所以,BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m)即它行驶的速度为108km/h.
勾股定理的实际应用--树折断问题
例2. 如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
解:在Rt△ACB中,由勾股定理,得AB2=BC2+AC2,
设AC=x米,则AB=(18-x)米∴(18-x)2=62+x2解得,x=8∴AC=8米答:这棵树折断后有8米高.
勾股定理的实际应用--折叠问题
例3. 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
解:由折叠可得,AF=AD=BC=10cm,DE=EF
在Rt△ACF中,BF2=AF2-AB2 =102-82=36∴BF=6cm, ∴CF=4cm,
在Rt△ACF中,EF2=EC2+FC2设EC=xcm,则EF=DE=(8-x)cm,∴(8-x)2=x2+42解得,x=3即EC=3cm.
勾股定理解题思路:1. 在Rt△ABC中,a,b是两直角边,c为斜边,如果已知a,b,那么c2=_________;如果已知a,c,那么b2=_______;如果已知b,c,那么a2=_______,直接代入求解.2. 在Rt△ABC中,当不能直接运用勾股定理求线段长度时,则设所求线段的长度为x,根据两线段的关系(和差或倍分)用含x的代数式表示另一线段的长度,根据 ,列出含 的方程求解.
勾股定理 a2+b2=c2
运用勾股定理解决实际问题的一般步骤:1.从实际问题中抽象出几何图形;2. 确定要求的线段所在的直角三角形;3. 当已知两边时,直接根据勾股定理求第三边; 当已知一边及另两边关系时,依据勾股定理为等量关系建立方程求解.
1. 下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是 ( )
2. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是 ( ) A.72 B.52 C.80 D.76
3. 赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为 .
解析:如图所示:∵(a+b)2=21,∴a2+2ab+b2=21,∵大正方形的面积为13,2ab=21-13=8,∴小正方形的面积为13-8=5.
4. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为 17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了 米.
解析:在Rt△ABC中,∠CAB=90°,所以AB2=BC2-AC2=172-82=152,所以AB=15米.
在Rt△CAD中,∠CAD=90°,所以AD2=CD2-AC2=102-82=62,所以AD=6米,
所以BD=AB-AD=15-6=9(米),即船向岸边移动了9米.
5. 两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
解:根据题意如图所示,两棵树的高度分别为AB=8 m,CD=2 m,两棵树之间的距离BD=8 m,
过点C作CE⊥AB于点E,连接AC. 则BE=CD=2 m,EC=BD=8 m, AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理得,AC2=AE2+EC2=62+82=100,∴AC=10 m.答:这只小鸟至少要飞10 m.
6. 如图,一条小巷的左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )A.2.7米B.2.5米C.2米 D.1.8米
7. 如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,求水的深度?
解:如图,红莲被吹至一边,花朵刚好齐及水面即AC为红莲的长.设水深h尺,由题意得:Rt△ABC中,AB=h,AC=h+3,BC=6,由勾股定理得:AC2=AB2+BC2,即(h+3)2=h2+62,解得,h=4.5.答:水深4.5尺.
1. 用直角三角形和正方形通过拼图进行验证(利用两次计算面积,即图形整体面积等于各部分面积之和)
2. 根据勾股定理(1)已知直角三角形的任意两边求第三边; (2)已知直角三角形的任意一边及另两边的关系构造方程求线段长.
2002年的数学家大会(ICM-2002)在北京召开,这届大会会标 的中央图案正是经过艺术处理的弦图,这既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们!
数学八年级上册1 探索勾股定理精品ppt课件: 这是一份数学八年级上册1 探索勾股定理精品ppt课件,共36页。
初中数学北师大版八年级上册1 探索勾股定理优质课件ppt: 这是一份初中数学北师大版八年级上册1 探索勾股定理优质课件ppt,共31页。PPT课件主要包含了勾股树,导入新知,素养目标,勾股定理的探索,做一做,探究新知,数格子,单位面积,4分析填表数据,勾股定理等内容,欢迎下载使用。
初中数学北师大版八年级上册1 探索勾股定理教案配套ppt课件: 这是一份初中数学北师大版八年级上册1 探索勾股定理教案配套ppt课件,共17页。PPT课件主要包含了探索勾股定理,Contents,情景导入,情境导入,新知探究,S浅蓝色正方形b2,S紫色正方形a2,S绿色正方形c2,c2a2+b2,巩固练习等内容,欢迎下载使用。













