初中第一章 勾股定理1 探索勾股定理课后练习题

这是一份初中第一章 勾股定理1 探索勾股定理课后练习题，文件包含答案1docx、原卷1docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

北师大版 数学 八上 第一章 1.1探索勾股定理测试提升卷
一， 选择题（共30分）
1.若直角三角形的两边长分别是5和12，则它的斜边长是(　　)
A．13 B．13或 119 C．119 D．12或13
【答案】D
【知识点】勾股定理
【解析】【解答】解：①当12为斜边时，它的斜边长是12；
②当12是直角边时，它的斜边长=122+52=13.
故答案为：D.

2.如图，已知钓鱼竿 AC 的长为 10m ，露在水面上的鱼线 BC 长为 6m ，某钓鱼者想看看鱼钩上的情况，把鱼竿 AC 转动到 AC′ 的位置，此时露在水面上的鱼线 B′C′ 为 8m ，则 BB′ 的长为（　　）

A．1m B．2m C．3m D．4m
【答案】B
【知识点】勾股定理
【解析】【解答】解：∵AC=10m，BC=6m，∠ABC=90°，
∴AB= AC2−BC2=102−62=8 m，
∵AC′=10m，B′C′=8m，∠AB′C′=90°，
∴AB′= AC'2−B'C'2=102−82=6 m，
∴BB′=AB-AB′=2m；
故答案为：B．

3.如图，在△ABC中，∠ACB=90°，点D是AB的中点，连接CD，若AC=4，BC=3，则CD的长度是（　　)

A．1.5 B．2 C．2.5 D．5
【答案】C
【知识点】勾股定理；直角三角形的性质
【解析】【解答】解：∵△ABC 中， ∠ACB=90° ， AC=4，BC=3，
由勾股定理得：AB=AC2+BC2=42+32=5,
∵点D是AB的中点 ，
∴CD=12AB=12×5=2.5，
故答案为：C.

4.如图，在长方形ABCD中，分别按图中方式放入同样大小的直角三角形纸片．如果按图①方式摆放，刚好放下4个；如果按图②方式摆放，刚好放下3个．若BC＝4a，则按图③方式摆放时，剩余部分CF的长为（　　）

A．2a3 B．3a2 C．5a3 D．3a5
【答案】A
【知识点】勾股定理；线段的计算
【解析】【解答】解：∵BC=4a，
∴图①中，BE=a，图②中，BE=43a，
∴小直角三角形的斜边长为a2+(43a)2=53a，
∴图③中纸盒底部剩余部分CF的长为4a-2×53a=23a；
故答案为：A．


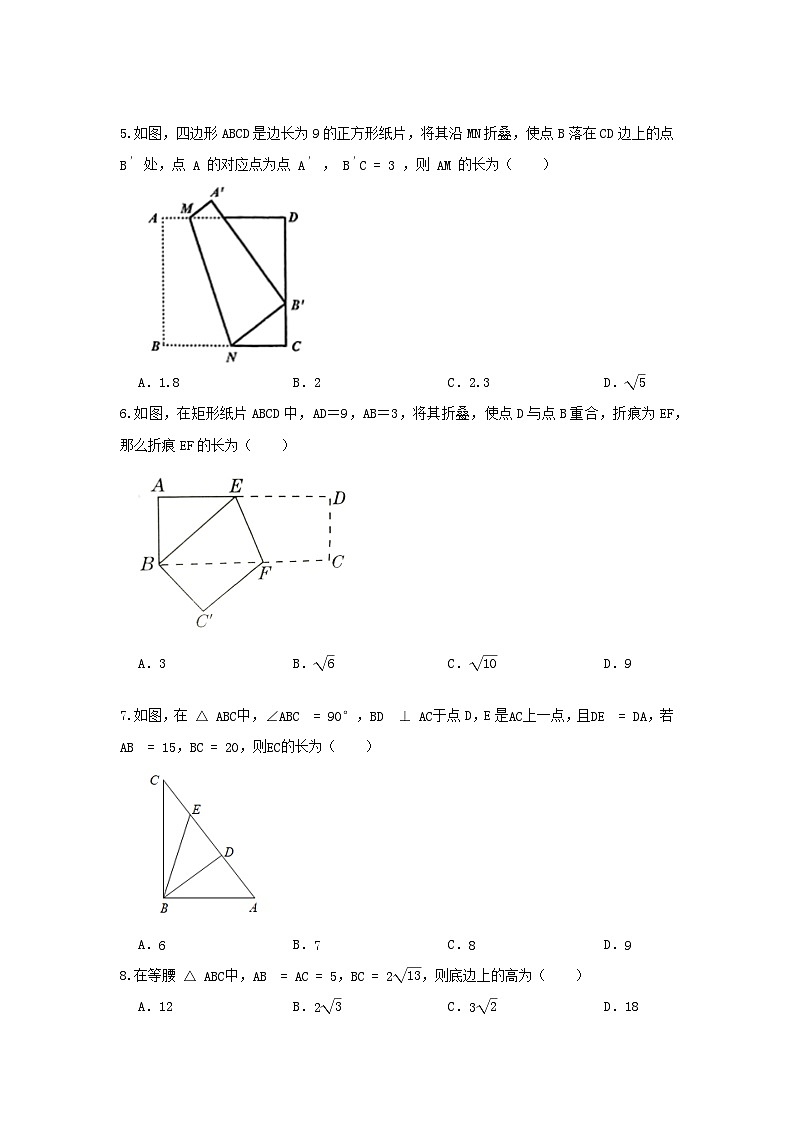
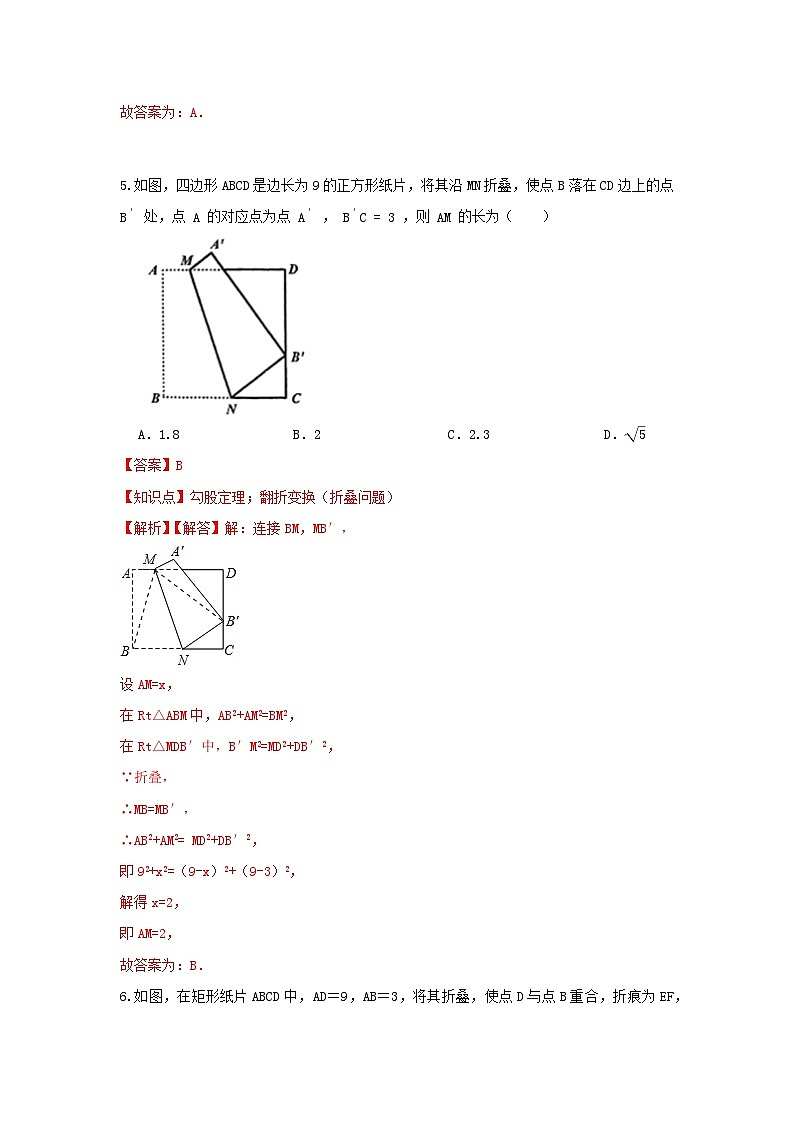
5.如图，四边形 ABCD 是边长为9的正方形纸片，将其沿 MN 折叠，使点 B 落在 CD 边上的点 B′ 处，点 A 的对应点为点 A′ ， B′C=3 ，则 AM 的长为（　　）

A．1.8 B．2 C．2.3 D．5
【答案】B
【知识点】勾股定理；翻折变换（折叠问题）
【解析】【解答】解：连接BM，MB′，

设AM=x，
在Rt△ABM中，AB2+AM2=BM2，
在Rt△MDB′中，B′M2=MD2+DB′2，
∵折叠，
∴MB=MB′，
∴AB2+AM2= MD2+DB′2，
即92+x2=（9-x）2+（9-3）2，
解得x=2，
即AM=2，
故答案为：B．
6.如图，在矩形纸片ABCD中，AD＝9，AB＝3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为（　　）

A．3 B．6 C．10 D．9
【答案】C
【知识点】勾股定理；翻折变换（折叠问题）
【解析】【解答】解：过点F做FH⊥AD交AD于点H．

∵四边形EFCB是四边形EFCD沿EF折叠所得，
∴ED=BE，CF=CF，BC'=CD=3
∵ED=BE，DE=AD-AE=9-AE
∴BE=9-AE
∵Rt△ABE，AB=3，BE=9-AE
∴(9−AE)2=32+AE2
∴AE=4
∴DE=5
∴CF=BC−BF=9−BF
∴Rt△BCF，BC=3，CF=9−BF
∴(9−BF)2+32=BF2
∴BF=5，EH=1
∵Rt△EFH，HF=3，EH=1
∴EF=EH2+HF2=32+12=10
故答案为：C．

7.如图，在△ABC中，∠ABC=90°，BD⊥AC于点D，E是AC上一点，且DE=DA，若AB=15，BC=20，则EC的长为（　　）

A．6 B．7 C．8 D．9
【答案】B
【知识点】勾股定理；线段的计算
【解析】【解答】解：在Rt△ABC中，∠ABC=90°，
∴AB2+BC2=AC2．
∵BC=20，AB=15，
∴AC=25，
∵BD⊥AC，
∴∠ADB=90°．
∵S△ABC=S△ABC，
∴12AB⋅BC=12AC⋅BD，
∴BD=12，
在Rt△ABD中，AD=AB2−BD2=152−122=9，
∵DE=DA，
∴AE=2AD=18．
∴EC=AC−AE=25−18=7．
故答案为：B.

8.在等腰△ABC中，AB=AC=5，BC=213，则底边上的高为（　　）
A．12 B．23 C．32 D．18
【答案】B
【知识点】等腰三角形的性质；勾股定理
【解析】【解答】解：如图，过点A作AD⊥BC于点D，

∵△ABC是等腰三角形，AB=AC，
∴BD=CD=12BC=13，
在Rt△ABD中，由勾股定理得，
AD=AB2−BD2=52−(13)2=23，
即底边上的高为23，
故答案为：B．

9.如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则 MC2−MB2等于(　　)

A．9 B．35 C．45 D．无法计算
【答案】C
【知识点】勾股定理
【解析】【解答】解：∵AD⊥BC，
∴∠ADB=∠ADC=90°，
在Rt△ABD和Rt△ADC中，
BD2＝AB2-AD2，CD2＝AC2-AD2，
在Rt△BDM和Rt△CDM中，
BM2＝BD2+MD2＝AB2-AD2+MD2，MC2＝CD2+MD2＝AC2-AD2+MD2，
∴MC2-MB2＝（AC2-AD2+MD2）-（AB2-AD2+MD2）＝AC2-AB2
又∵AB=6，AC=9，
∴MC2-MB2＝45．
故答案为：C．

10.如图，一个梯子斜靠在一竖直的墙AO上，测得AO＝4m，若梯子的顶端沿墙下滑1m，这时梯子的底端也下滑1m，则梯子AB的长度为（　　）

A．5m B．6m C．3m D．7m
【答案】A
【知识点】勾股定理
【解析】【解答】解：设BO＝xm，
由题意得：AC＝1m，BD＝1m，AO＝4m，
在Rt△AOB中，根据勾股定理得：AB2＝AO2+OB2＝42+x2，
在Rt△COD中，根据勾股定理得：CD2＝CO2+OD2＝（4﹣1）2+（x+1）2，
∴42+x2＝（4﹣1）2+（x+1）2，
解得：x＝3，
∴AB=AO2+BO2=42+32=5(m) ，
即梯子AB的长为5m，
故答案为：A．

二．填空题（共24分）
11.设x>0，若以x+1，x+2，x+3为边长的三角形是直角三角形，则x的值为　 　．
【答案】2
【知识点】勾股定理
【解析】【解答】解：由题意得斜边为x+3，
∴ (x+1)2+(x+2)2=(x+3)2，
∴x2=4，
解得x=2或-2（舍去）.
故答案为：2.

12.如图，在 △ ABC中，AB＝20，AC＝15，BC＝7，则点A到BC的距离是　 　.

【答案】12
【知识点】勾股定理
【解析】【解答】解：过A作AD⊥BC交BC的延长线于D，

∴∠D=90°，
∴AB2− BD2=AD2=AC2− CD2，
∵AB=20，AC=15，BC=7，
∴202− （7+CD）2=152− CD2，
∴CD=9，
∴AD=152−92=12 ，
∴点A到BC的距离是12；
故答案为：12.

13.如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt△ABC中，∠C=90° ，AC=2，若Rt△ABC是“好玩三角形”，则AB=　 　．
【答案】7或2213
【知识点】勾股定理；定义新运算
【解析】【解答】解：当AC边上的中线BD等于AC时，如图，

∵∠C=90°，AC=2，
∴CD=1,BD=2
∴BC2=BD2−CD2=22−12=3,
∴AB=AC2+BC2=22+3=7
当BC边上的中线AE等于BC时，
∵AC2=AE2−CE2，
∴BC2−（12BC）2=22，
解得，BC2=163，
∴AB=AC2+BC2=22+163=2213,
综上所述，AB=7或AB=2213,
故答案为7或2213.

14.如图，在长方形ABCD中，AB=9，AD=14．点E、点F分别在AD、BC上，且AE=CF=1，点G是DC边上的动点，点H是AB边上的动点．则EG+HG+HF的是小值是　 　．

【答案】41
【知识点】勾股定理；矩形的性质；轴对称的应用-最短距离问题
【解析】【解答】作点E关于CD的对称点E'，点F关于AB的对称点F'，

则EG= E'G，HF=HF'，
∴EG+HG+HF=E'G+HG+HF'，
连接E'F'，交AB、CD于H、G点，BG+HG+HF的最小值即为E'F'的长，
过点E'作E'H⊥BC，交BC的延长线于H，
则F'H=14+2×13=40，E'H =9，
在Bt△FH中，由勾股定理得E'F'=92+402=41，
∴BG+G+HF的最小值为：41，
故答案为：41．

15.三角形的两条边长分别为3cm、4cm，则这个直角三角形的斜边长为　 　cm.
【答案】4或5
【知识点】勾股定理
【解析】【解答】解：∵3<4 ，
∴当4是斜边时，斜边长就是4；
当4是直角边时，斜边是： 32+42=5 ，
综上所述，这个直角三角形的斜边长为：4或5
答案是：4或5.

16.如图，在Rt△ABC中，∠B=90°，分别以A，C为圆心，大于12AC长为半径画弧，两弧相交于点M，N，作直线MN，与AC，BC分别交于点D，点E，连结AE，当AC=13，AB=5时，则△ABE的周长是　 　.

【答案】17
【知识点】线段垂直平分线的性质；勾股定理
【解析】【解答】解：∵Rt△ABC中，∠B=90°，AC=13，AB=5，
∴BC=AC2−AB2=12，
由作法得MN垂直平分AC，
∴EA=EC，
∴△ABE的周长=AB+BE+AE=AB+BE+CE=AB+BC=5+12=17.
故答案为：17.

三． 解答题（共46分）
17.（8分）如图，甲乙两船从港口A同时出发，甲船以16海里/时速度向北偏东40°航行，乙船向南偏东50°航行，3小时后，甲船到达C岛，乙船到达B岛．若C、B两岛相距60海里，问乙船的航速是多少．

【答案】解：根据题意，得∠CAB=180°-40°-50°=90°，
∵AC=16×3=48（海里），BC=60海里，
∴在直角三角形ABC中，根据勾股定理得：AB=602−482 =36（海里）．
则乙船的速度是36÷3=12海里/时．

18.（8分）已知△ABC中，AB＝AC，CD⊥AB于D，若AB＝5，CD＝3，求BC的长．

【答案】解：在Rt△CDA中， ∵AC=AB=5，CD=3，
∴AD= AC2−CD2=4,
∴BD=AB-AD=5-4=1，
在Rt△CBD中，BC= CD2+BD2=12+32=10.

19.（10分）已知，如图，在△ABC中，∠C＝ 90°，AD平分∠BAC交BC于D，过D作DE∥AC交AB于E．

（1）求证：AE＝DE；
（2）如果AC＝3，AD=23，求AE的长．
【答案】（1）证明：∵DE∥AC，
∴∠CAD＝∠ADE．
∵AD平分∠BAC，
∴∠CAD＝∠EAD．
∴∠EAD ＝∠ADE．
∴AE＝DE．
（2）解：过点D作DF⊥AB于F．

∵∠C ＝ 90°，AC＝3，AD=23，
∴在Rt△ACD中，由勾股定理得 AC2+DC2=AD2．
∴DC=3．
∵AD平分∠BAC，
∴DF＝DC＝3．
又∵AD＝ AD，∠C ＝ ∠AFD ＝ 90°，
∴Rt△DAC ≌Rt△DAF．
∴AF＝AC＝3．
∴Rt△DEF中，由勾股定理得 EF2+DF2=DE2．
设AE＝x，则DE＝x，EF=3−x，
∴(3−x)2+(3)2=x2，
∴x＝2．
∴AE＝2．

20.（10分）十一国庆节，某校各班都在开展丰富多彩的庆祝活动，八年级（1）班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．武玥同学在制作手工作品的第一、二个步骤是：

①先裁下了一张长 BC=20cm ，宽 AB=16cm 的长方形纸片 ABCD ；
②如图，将纸片沿着直线 AE 折叠，点 D 恰好落在 BC 边上的 F 处．
请你根据①②步骤计算 EC ， FC 的长．
【答案】解：∵△ADE由△AFE关于AE对称，
∴△ADE≌△AFE，
∴DE=FE，AD=AF，
∵四边形 ABCD 是矩形，
∴BC=AD=AF=20cm，AB=CD=16cm，
在Rt△ABF中，由勾股定理： BF=AF2−AB2=202−162=12 cm，
∴CF=BC-BF=20-12=8cm．
∵四边形ABCD是矩形，
∴∠C=90°．
设CE=x，则DE=EF=16-x，
在Rt△CEF中，由勾股定理： EF2=CE2+CF2 ，代入数据：
(16-x)2=x2+64，
解得：x=6．
∴EC=6cm．
综上所述，线段EC=6cm，CF=8cm．


21.（10分）问题背景

（1）如图1，点P是线段AB，CD的中点，求证：AC∥BD；
（2）【变式迁移】
如图2，在等腰△ABC中，BD是底边AC上的高线，点E为△ABD内一点，连接ED，延长ED到点F，使ED=FD，连接AF，若BE⊥AF，若AB=10，EB=6，求AF的长；
（3）【拓展创新】
如图3，在等腰△ABC中，∠ACB=90°，AC=BC，点D为AB中点，点E在线段BD上（点E不与点B，点D重合），连接CE，过点A作AF⊥CE，连接FD，若AF=8，CF=3，请直接写出FD的长.
【答案】（1）证明：∵点P是线段AB，CD的中点，
∴PA=PB，PD=PC，
在△PAC和△PBD中，
PA=PB∠APC=∠BPDPC=PD
∴△PAC≌△PBD(SAS)，
∴∠A=∠B，
∴AC∥BD；
（2）解：如图：连接CE，

∵在等腰△ABC中，BD是底边AC上的高线，
∴AD=DC，
在△ADF和△CDE中，
DF=DE∠ADF=∠CDEAD=CD
∴△ADF≌△CDE(SAS)，
∴∠FAD=∠ECD，AF=CE，
∴AF∥CE，
∵BE⊥AF，
∴BE⊥CE，
∵AB=BC=10，BE=6，
∴CE=BC2−BE2=102−62=8，
∴AF=8；
（3）解：522
【知识点】平行线的判定与性质；三角形全等的判定；勾股定理
【解析】【解答】解：（3）如图：延长FD到T，使得DT=DF，连接BT，延长CE交BT于点J.

∵点D为AB中点，
∴AD=BD，
在△ADF和△BDT中，
DF=DT∠ADF=∠BDTAD=DB
∴△ADF≌△BDT(SAS)，
∴AF=BT=8，∠T=∠AFD，
∴AF∥BT，
∵AF⊥CJ，
∴CJ⊥BT，
∴∠AFC=∠CJB=∠ACB=90°，
∵∠ACF+∠BCJ=90°，∠BCJ+∠CBJ=90°，
∴∠ACF=∠CBJ，
又∵AC=CB，
∴△AFC△CJB(AAS)，
∴CF=BJ=3，AF=CJ，
∴CJ=BT=8，
∴FJ=JT=8−3=5，
∵∠FJT=90°，
∴FT=2FJ=52，
∴DF=12FT=522.