


【同步教案】北师大版数学八年级上册--1.1 勾股定理的图形验证 教案
展开第一章 勾股定理
1.1 探索勾股定理(第2课时)
一、学生起点分析
学生的知识技能基础:学生在上节课已经通过测量和数格子的方法,对特殊的直角三角形进行了探索并发现了勾股定理,但没有对一般的直角三角形进行一般性的验证.
学生活动经验基础:学生具有了一定的自主探究经验和合作学习的经验,具备了一定的探究能力和合作与交流的能力;尤其在在七年级《图案设计》的学习中已经具备了一定的拼图活动经验.
二、教学任务分析
本节课是八(上)勾股定理第1节第2课时,是在上节课已探索得到勾股定理之后的内容,具体学习任务:通过拼图验证勾股定理并体会其中数形结合的思想;应用勾股定理解决一些实际问题,体会勾股定理的应用价值并逐步培养学生应用数学解决实际问题意识和能力 ,为后面的学习打下基础.为此本节课的教学目标是:
1.了解勾股定理的历史,感受数学文化;
2.探究验证勾股定理的三类方法:(1)等面积,两算法;(2) 无字的证明;(3)欧氏几何证明;
3.能初步应用勾股定理解决一些实际问题.
4.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想, 培养学生的探究能力和合作精神.
教学重点: 探究验证勾股定理的三类方法
教学难点: 验证勾股定理的三类方法
三、教学过程
本节课设计了七个教学环节:
(一)史话勾股定理;(二)探究勾股定理的三类证明方法;(三)例题讲解,勾股定理的初步应用;(四)课堂练习;(五)拓展延伸;(六) 反思小结;(七)布置作业
第一环节: 史话勾股定理
1.观看关于勾股定理历史的视频
视频大致内容:3000多年前 ,古巴比伦人和古埃及人都已经对发现了勾股定理,在我国1000多年前,周朝数学家商高在提出了:“勾广三,股修四,经隅五”的勾股定理的特例,最早给出证明的是公元前6世纪古希腊数学家毕达哥拉斯,公元前4世纪,欧几里德在«几何原本»中给出了一种很好的证明,在我国最早给出证明的是公元前三世纪的数学家赵爽,稍后一时期的刘徽在«九章算术»用“青朱出入图”这种无字的证明方法验证了勾股定理。直到现在有500多种证明方法,今天就让我们沿着历史的足迹探究勾股定理。
第二环节: 探究勾股定理的证明方法
第一种类型:等面积 两算法
方法一:毕达哥拉斯的证明
1 问题背景

相传有一天,毕达哥拉斯去朋友家里做客,发现朋友家的地砖是方砖,他在方砖上画了一个等腰直角三角形,并以三条边向外做了三个正方形,聪明的毕达哥拉斯发现:以直角边为边的两个正方形的面积的和等于以斜边为边的正方形的面积。由此,他猜想:任意一个直角三角形,两条直角边的平方和都等于斜边的平方。
2. 探究思路与方法
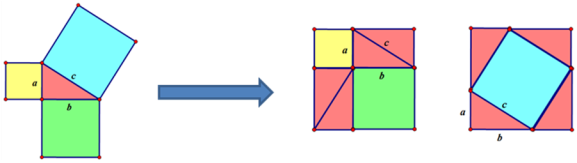
图1
(1)如图1你能表示两个大正方形的面积吗?
(2)你能由此得到勾股定理吗?为什么?(板书)
a2+b2+4×![]() ab =c2+4×
ab =c2+4×![]() ab2,并得到
ab2,并得到![]()
方法二:赵爽弦图
1历史背景




在我国最早给出证明的是公元前三世纪的数学家赵爽,他在周髀算经中用一张他所谓的弦图证明了勾股定理,2002年全世界数学家大会的会徽就是这张弦图,以此纪念这位伟大的数学家。
2 探究赵爽弦图的思路与方法

图2
(1) 如图2,用几何画板演示将两个小正方形拼成赵爽弦图;
(2) 小组交流拼出赵爽弦图,你能用两种方法表示这个图形的面积吗?(学生板书并讲解)
(b-a)2+4×![]() ab =c2,得到
ab =c2,得到![]()
第二种类型:无字证明
方法三:青朱出入图(无字的证明)
1 历史背景

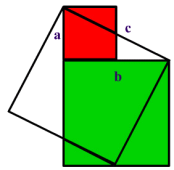

比赵爽稍微晚些的数学家刘徽在«九章算术»用“青朱出入图”验证了勾股定理,由于证明过程没有用一个字,因此把这种证明又称为无字的证明。
2 探究青朱出入图的与方法

图3
如图3,用几何画板演示青朱出入图验证勾股定理的过程。
第三种类型:欧氏几何证明
方法四:欧几里得证明
1历史背景


公元前4世纪,欧几里德在«几何原本»中给出了一种很好的证明
2 探究欧几里德证明的思路与方法

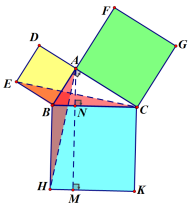
图4
(1) 如图4:教师分析思路并给出辅助线方法,
从Rt△ABC的三边向外各作一个正方形(如图4),作AN⊥BC交AB于N,那么正方形ABED被分成两个矩形.连结AH和EC.
(2)小组交流验证方法 (多媒体展示)
∵由于矩形BNHM和△ABH同底等高∴S矩形BNHM=2S△ABH
又∵正方形ABED和△EBC同底等高∴S正方形ABED=2S△EBC.
又∴△EBC≌△ABH.
由此可得S矩形BHMN=S正方形ABED
同理可证S矩形NCMK=S正方形AFGC
∴S矩形BHMN+S矩形NCMK=S正方形ABED+S正方形AFGC
即S正方形BHCK=S正方形ABED+S正方形AFGC,
也就是 a2+b2=c2.
总结勾股定理的证明方法:分三种类型
第一种类型:等面积 两算法
以赵爽的“弦图”为代表,用几何图形的 截、割、拼、补,一图两算来证明代数式之间的恒等关系;
第二种类型:无字证明
以刘徽的“青朱出入图”为代表,“无字证明”。
第三种类型:欧氏几何证明
欧氏几何证明以欧几里得的证明方法为代表,运用欧氏 几何的基本定理进行证明;
第三环节: 勾股定理的应用
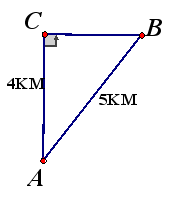 例1: 如图5,飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4 km处,过了20 s,飞机距离这个男孩子头顶5 km,飞机每小时飞行多少千米?
例1: 如图5,飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4 km处,过了20 s,飞机距离这个男孩子头顶5 km,飞机每小时飞行多少千米?
解:Rt △ ABC中,由勾股定理得:
AB2 = BC2 + AC2 即 52 = BC2 + 42,
所以 BC=3
飞机20 s飞行了3 km,那么1小时飞行的距离为:
3 x 3 x 60= 540 km,
即:飞机 每小时飞行540 km。 图5
第四环节: 课堂练习
1.如图6,三个正方形中其中两个面积S2、S3分别为 144、169,则第三个正方形的面积S1为____。


图6 图7
2.如图7,是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接B,C,E三城市的沿江高速,已知沿江高速的建设成本是100万元/ km,该沿江高速的造价预计是多少?
解:Rt △ ABC中,由勾股定理得: BC2 =A B2 + AC2
即BC 2 =30 2 + 402, 所以 BC=50
Rt △ CDE中,由勾股定理得: CE2 =CD2 + DE2
即CE 2 =50 2 + 1202, 所以 CE=130
所以 BE=BC+CE=180 KM
180 x 100=18000 万元
即:该沿江高速的造价预计是18000 万元
第五环节: 拓展延伸
以小组为单位,用几何画板探究以下问题:
(1) 如图8,在前面已经讨论了直角三角形三边满足的关系,那么锐角三角形或钝角三角形的三边是否也满足这一关系呢?
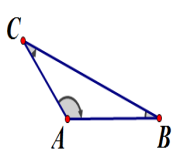
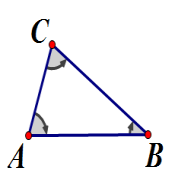
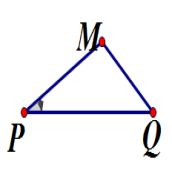
图8 图9
(2) 如图9,在任意一个三角形中,如果一个角是锐角,那么这个三角形中夹这个锐角两边的平方和与第三边的平方有怎样的大小关系呢?如果这个角是钝角呢?(以图中的∠ P 为例来探讨)
第六环节:课堂小结
1.验证勾股定理的三类方法:
第一种类型:等面积 两算法
第二种类型:无字证明
第三种类型:欧氏几何证明
2.勾股定理的初步应用
3.欣赏美丽的勾股树
在几何画板中欣赏动态勾股树,感受数学中的美!
第七环节:布置作业
1必做题:
习题1.2: 第1、2 、3题
2选做题:
搜集有关勾股定理的证明方法并选择其中一种方法仔细研究。









