

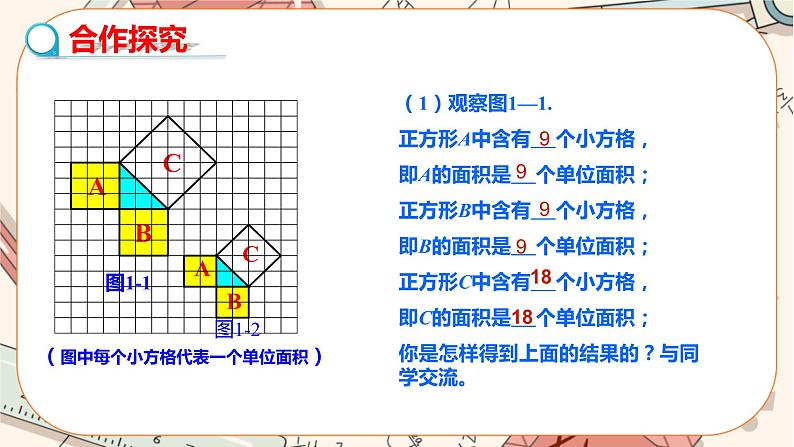
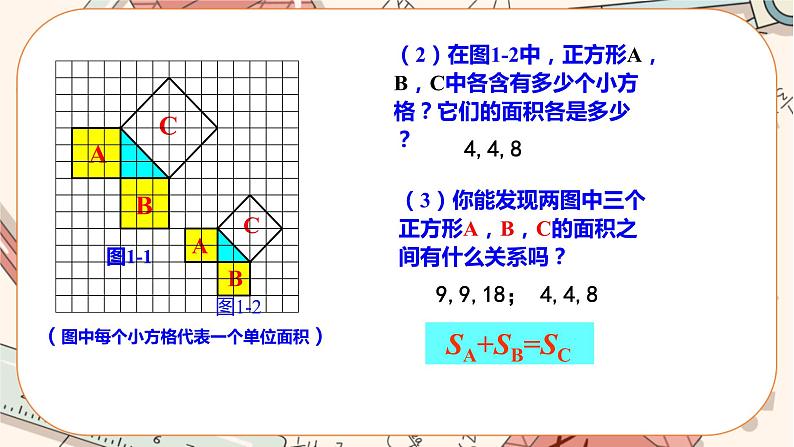
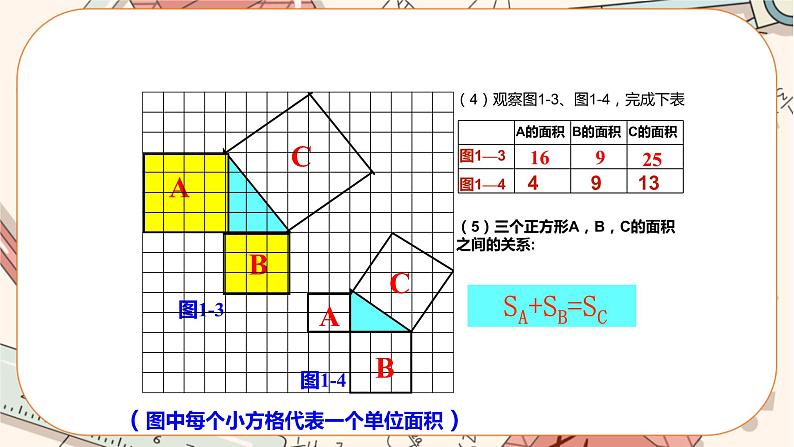
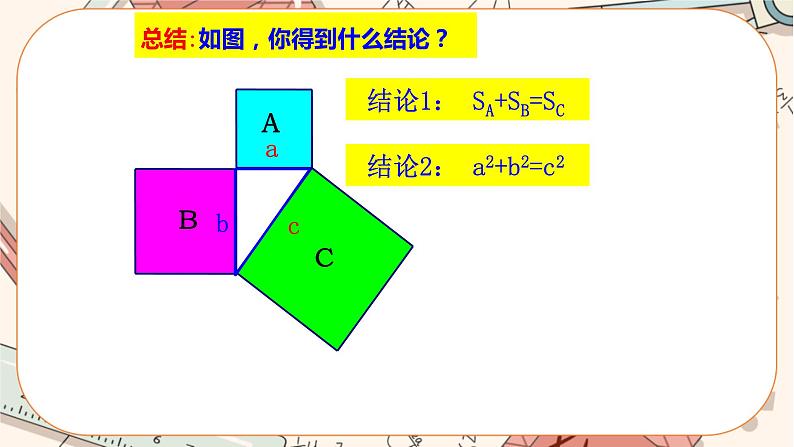
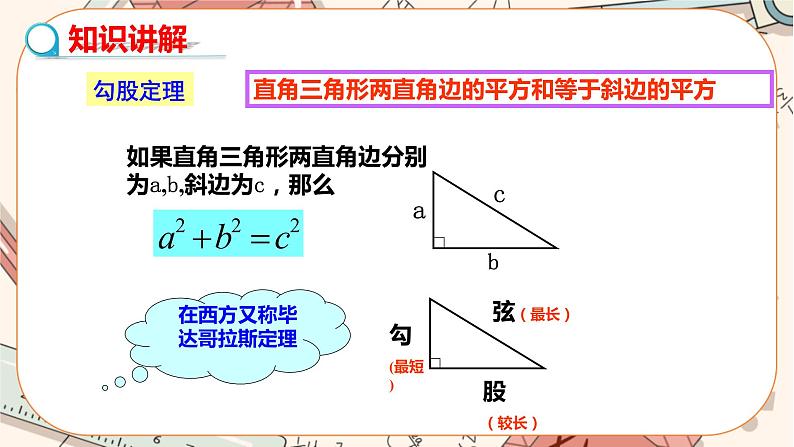

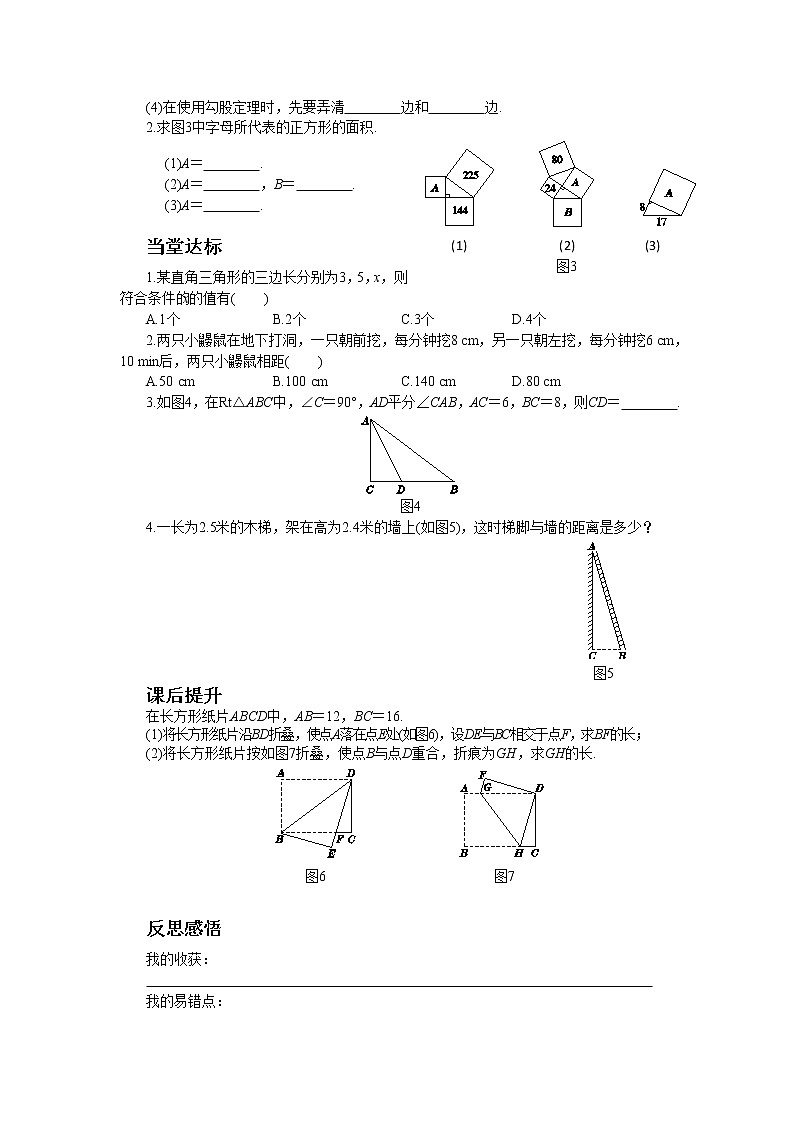


初中数学北师大版八年级上册第一章 勾股定理1 探索勾股定理精品课件ppt
展开第一章 勾股定理
1 探索勾股定理
第2课时 勾股定理的证明及应用
教学目标 1.经历运用拼图的方法说明勾股定理是正确的过程,在教学活动中发展学生的探究意识和合作交流的习惯. 2.通过对勾股定理的探索,在探索实践中理解并掌握勾股定理并且会运用勾股定理. 教学重难点 重点:会验证勾股定理,并能应用勾股定理解决一些实际问题. 难点:经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想. 教学过程 导入新课 教师提出问题: 1.勾股定理的内容是什么?(指名学生回答) 2.上节课我们仅仅是通过测量和数格子,对具体的直角三角形进行探索发现了勾股定理,对一般的直角三角形勾股定理是否成立呢?这需要进一步验证,如何验证勾股定理呢? 教师:事实上,现在已经有数百种勾股定理的验证方法,这节课我们就来验证一下勾股定理. 设计意图:回顾上节课探索过程,强调仍需对一般的直角三角形进行验证,培养学生严谨的科学态度,介绍世界上一些验证方法,激发学生的学习兴趣. 探究新知 一、预习新知 让学生自主预习课本第5页. 提出问题:如下图,分别以直角三角形的三条边为边向外作正方形,你能利用这幅图说明勾股定理的正确性吗? 先让学生独立作图、验证,并让学生发表自己的见解,再小组讨论勾股定理是否正确. 设计意图:通过让学生自己动手作图、验证不仅能锻炼学生的动手能力,还能加深对勾股定理的理解. 二、合作探究 验证勾股定理 为了计算上图中大正方形的面积,小明对这个大正方形进行了适当割补后得到了下面两个图.
图1 图2 问题1:你可以利用两种方法来表示图1中的大正方形的面积吗? 学生先独立思考,再小组交流得到答案和2ab+ 问题2:你可以得到怎样的等式?从而能得到什么? 学生: = 2ab+,化简后得到. 从而利用图1验证了勾股定理,此方法称为毕达哥拉斯法. 教师:我们利用拼图的方法,将形的问题与数的问题结合起来,利用整式运算的有关知识,从理论上验证了勾股定理,你还能利用图2验证勾股定理吗? 问题3:图2中小正方形的边长是多少? 问题4:你可以利用两种方法来表示图2中的大正方形的面积吗? 问题5:你可以得到怎样的等式?从而能得到什么? 提出几个问题让学生根据问题独立探究,再小组交流,最后请一位同学上台讲解利用图2验证勾股定理. 图2中小正方形边长是b-a,和都可以表示图2中小正方形的面积,根据同一图形面积相等得到,化简后得到. 从而利用图2也验证了勾股定理,图2我们又称为赵爽弦图. 设计意图:教师层层设问引导学生来完成勾股定理的验证,通过两个图形让学生体会数形结合的思想并体会成功的快乐,学生先拼图从形上感知,再利用面积验证,比较容易掌握本节课的重点内容. 前面已经讨论了直角三角形的三边长满足的关系,那么锐角三角形和钝角三角形是否也满足这一关系呢? 观察下图,利用数格子的方法判断图中三角形的三边长是否满足. 学生通过数格子的方法可以得出,如果一个三角形不是直角三角形,那么它的三边长a,b,c不满足,通过这个结论,学生将对直角三角形的三边关系有进一步认识. 巩固练习 根据下图,利用面积法证明勾股定理. 证明:∵ S梯形ABCD = S△ABE+S△BCE+S△EDA, 又∵ S梯形ABCD = (a+b)2,S△BCE = S△EDA = ab,S△ABE = c2, ∴ (a+b)2 = 2×ab+c2, ∴ a2+b2 = c2,即勾股定理得证. 典型例题 【例1】作8个全等的直角三角形,设它们的两条直角边长分别为a,b,斜边长为c,再作三个边长分别为a,b,c的正方形,将它们如下图所示拼成两个正方形. 证明:a2+b2 = c2.
【问题探索】从整体上看,这两个大正方形的边长都是a+b,因此它们的面积相等.我们再用不同的方法来表示这两个正方形的面积,即可证明勾股定理. 【证明】由图易知,这两个正方形的边长都是a+b, ∴ 它们的面积相等. 左边大正方形面积可表示为a2+b2+ab×4, 右边大正方形面积可表示为c2+ab×4. ∵ a2+b2+ab×4 = c2+ab×4, ∴ a2+b2 = c2. 【总结】根据拼图,通过对拼接图形的面积的不同表示方法,建立相等关系,从而验证勾股定理. 典型例题 【例2】如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本为5 000万元/km,该沿江高速公路的造价预计是多少? 【问题探索】总造价计算公式是解决此题目的关键,总造价 = 每千米造价千米数. 【解】在Rt△OMN中,根据勾股定理得 MN 2+ON 2 = OM 2, ∴ 302+402 = OM 2, ∴ OM = 50 km. 同理OQ = 130 km, ∴ 造价为(50+130)5 000 = 900 000(万元). 答:造价预计是900 000万元. 【总结】解答本题的关键是先利用勾股定理求出高速公路的长度,再求总造价. 课堂练习 1.若等腰三角形的腰长为13 cm,底边长为10 cm,则它的面积为( ) A.30 cm2 B.130 cm2 C.120 cm2 D.60 cm2 2.放学以后,小丽和小红从学校出发,分别沿东南方向和西南方向回家.若小丽和小红行走的速度都是40 m/min,小丽走了15 min回到家,小红走了20 min回到家,则小丽家和小红家间的距离为( ) A.600 m B.800 m C.1 000 m D.不确定 3.直角三角形两直角边长分别为8 cm,15cm,则斜边上的高为______. 4.某农舍的大门是一个木制的矩形栅栏,它的高为2 m,宽为1.5 m,现在需要在相对的顶点间用一块木板加固,则这块木板的长为______. 5.如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1 = 2 km,BB1 = 4 km,A1B1 = 8 km.现要在高速公路上A1,B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离之和. 参考答案 1.D 2.C 3. cm 4.2.5 m 5.解:如图作点B关于MN的对称点B′, 连接AB′交A1B1于点P,连接BP. 则AP+BP = AP+PB′ = AB′, 易知点P即为到点A,B距离之和最短的点. 过点A作AE⊥BB′于点E, 则AE = A1B1 = 8 km,B′E = AA1+BB1 = 2+4 = 6( km). 由勾股定理,得B′A2 = AE 2+B′E 2 = 82+62, ∴ AB′ = 10 km,即AP+BP = AB′ = 10 km. 故出口P到A,B两村庄的最短距离之和是10 km.
课堂小结 (学生总结,老师点评) 勾股定理的内容:直角三角形两直角边的平方和等于斜边的平方. 验证方法:两种证法. 布置作业 1.(必做题)习题1.2第1,3题 2.(选做题)第4题 板书设计 1 探索勾股定理 第2课时 勾股定理的证明及应用 1.勾股定理:直角三角形两直角边的平方和等于斜边的平方. 2.两种证明方法.
|
初中数学北师大版八年级上册1 探索勾股定理优质课件ppt: 这是一份初中数学北师大版八年级上册1 探索勾股定理优质课件ppt,共31页。PPT课件主要包含了勾股树,导入新知,素养目标,勾股定理的探索,做一做,探究新知,数格子,单位面积,4分析填表数据,勾股定理等内容,欢迎下载使用。
北师大版八年级上册1 探索勾股定理优质课件ppt: 这是一份北师大版八年级上册1 探索勾股定理优质课件ppt,文件包含11探索勾股定理第2课时教学课件pptx、第一章勾股定理11探索勾股定理第2课时教学详案docx、11探索勾股定理第2课时学案+练习docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
数学八年级上册1 探索勾股定理课文内容ppt课件: 这是一份数学八年级上册1 探索勾股定理课文内容ppt课件,共23页。PPT课件主要包含了探索勾股定理,Contents,情境导入,巩固练习,课堂小结,新知探究,作业布置,测量法,数学小史,2符号语言等内容,欢迎下载使用。













