





北师大版八年级上册1 探索勾股定理教学ppt课件
展开情境问题:如图,从电线杆离地面8 m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索?
在直角三角形中,任意两边确定了,另外一条边也就随之确定,三边之间存在着一种特殊的数量关系.事实上,古人发现,直角三角形的三条边长度的平方存在一种特殊的关系,让我们一起探索吧!
1.1 探索勾股定理 第1课时 认识勾股定理
1. 用数格子(或割、补、拼)面积法探索勾股定理.2. 运用勾股定理进行简单的计算和应用.
问题1:观察下面地板砖示意图:你发现图中三个正方形的面积之间存在什么关系吗?
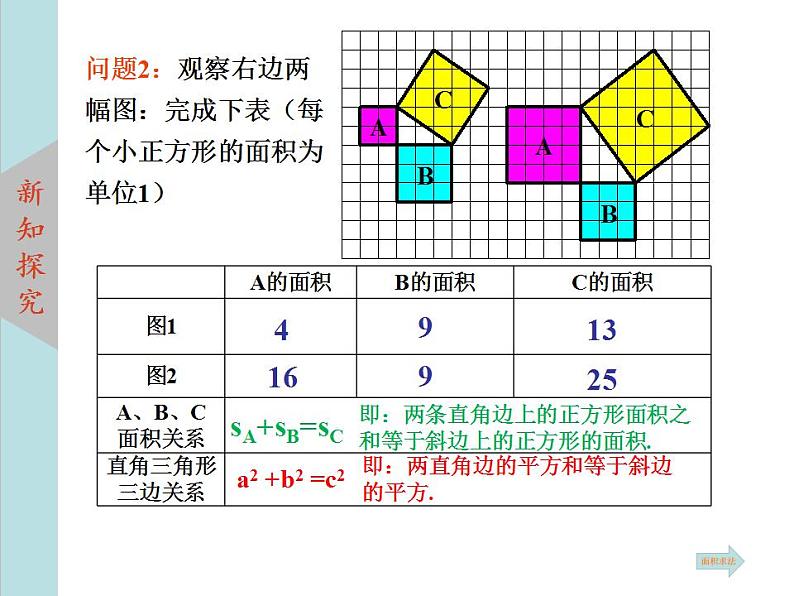
问题2:观察右边两幅图:完成下表(每个小正方形的面积为单位1)
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
即:两直角边的平方和等于斜边的平方.
勾股定理:直角三角形两直角边的平方和等于斜边的平方,如果用a,b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2
变式:a2=c2-b2 b2=c2-a2
勾股定理揭示了直角三角形三边之间的数量关系,是直角三角形的一个重要性质.
符号语言:∵∠ACB=90° ∴ a2+b2=c2
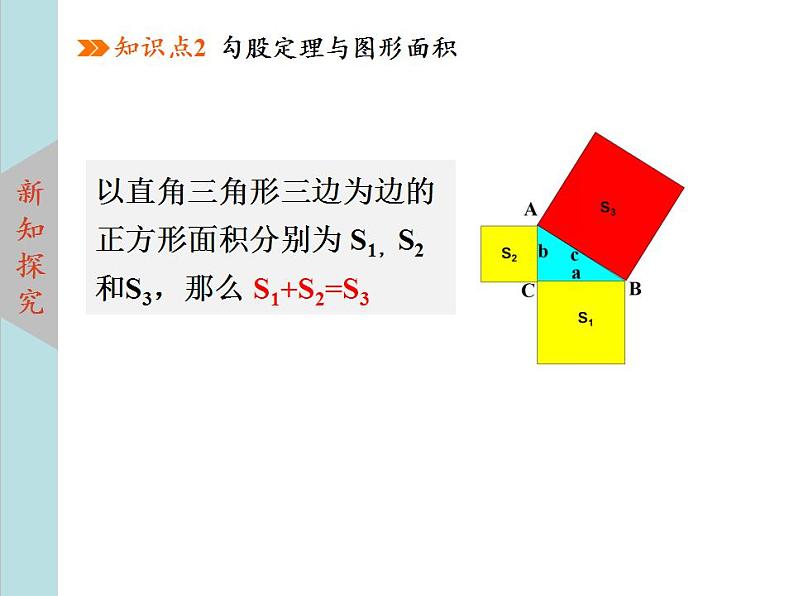
以直角三角形三边为边的正方形面积分别为 S1,S2和S3,那么 S1+S2=S3
利用勾股定理求直角三角形的边长
例1. 在Rt△ABC中,∠A,∠B,∠C 的对边 分别为a,b,c,∠C=90°.(1)已知a=3,b=4, 求c; (2)已知c=13,a=5,求b; (3)已知a:b=3:4,c=10,求b.
解:(1)∵∠C=90°,a=3,b=4, ∴由勾股定理,得
c2=a2+b2=32+42=25,
(2)已知c=13,a=5,求b;
∵∠C=90°,c=13,a=5, ∴由勾股定理,得
b2=c2-a2=132-52=144,
(3)已知a:b=3:4,c=10,求b.
分清待求的是斜边还是直角边,以便合理选择直接用勾股定理,还是用变形公式. 若求斜边,则直接用勾股定理;若求直角边,则用变形公式;若两边之间存在倍分或和差关系,则利用勾股定理建立方程求解.
∵a:b=3:4,∴b= a.
∵∠C=90°,c=10,∴由勾股定理,得 a2+( a)2= 102,
解得a=6(负值舍去). ∴b=8.
变式:在Rt△ABC中,∠A=90°,AB=24,BC=25,求AC的长.
解:在Rt△ABC中, 由勾股定理,得
AC2=BC2-AB2=252-242=49,
例2. 如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1,S2,S3,若S1+S2+S3=16,则S1的值为 .
解析:∵S1=S2+S3 且S1+S2+S3=16 ∴2S1=16, ∴S1=8.故答案为:8
变式一:如图,以Rt△ABC的三边为直径向外作半圆,其面积分别是S1,S2,S3,若S1=4π,S2=9π,则S3=______.
与直角三角形三边相连的正方形、半圆及正多边形、圆都具有相同的结论:两直角边上图形面积的和等于斜边上图形的面积.
解:S1=( a)2π× = a2 S2=( b)2π× = b2 S3=( c)2π× = c2
根据勾股定理a2+b2=c2,得S3=S1+S2=4π+9π=13π.故答案为:13π.
变式二:有一个边长为1的大正方形,经过1次“生长”后,在它的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过1次“生长”后,形成的图形如图所示.如果继续“生长”下去,它将变得“枝繁叶茂”,那么“生长”了2022次后形成的图形中,正方形D,E,F,G面积和是 ,生长了2022次图中所有的正方形面积和是 .
每一层正方形的面积和相等均为最大正方形面积.
应用勾股定理解决简单的实际问题
例3. 从电线杆离地面8 m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索?
解:如图,根据题意可得,∠ACB=90°,AC=8 m,BC=6 m,
由勾股定理得AB2=AC2+BC2=82+62=100
∴AB=10 m∴需要10 m的钢索.
1. 如图,下图中字母所代表的正方形的面积为A=_____,B=_____.
2. 若直角三角形两直角边之比为3:4,斜边长为20,则两条直角边分别为 ,_____,它的面积为_____.
3. 如图,已知△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为_____.
4. 如图所示的图形是由两个直角三角形和三个正方形组成的,其中阴影部分的面积是 ( )A.16 B.25 C.144 D.169
4. 求斜边为17cm,一条直角边长为15cm的直角三角形的面积.
∴S△ACB= AC·BC= ×15×8=60cm2.
解:在Rt△ACB中∠ACB=90°AB=17cm,AC=15cm由勾股定理得,BC2=AB2-AC2=172-152=64∴BC=8cm
5. 如图,求等腰三角形ABC的面积.
解:如图,过C作CD⊥AB,垂足为D,∵CD=CB=5cm,AB=6cm∴AD=DB=3cm,由勾股定理得,CD2=AC2-AD2=52-32=16∴CD=4cm
∴S△ABC= AB·CD= ×6×4=12cm2.
1. 直角三角形两直角边a,b与斜边c,求斜边时,c2=a2+b2;求直角边时,a2=c2-b2或b2=c2-a2,注意公式的变形.2. 求与直角三角形三边有关的图形面积时,要结合图形想办法把图形的面积与直角三角形三边的平方联系起来,再利用勾股定理找到图形面积之间的数量关系.
“割补法”将方格纸中的正方形变成若干个边长为整数的三角形或者正方形,再进行计算.
正方形周边上的格点数a=12
正方形内部的格点数b=13
所以,正方形C的面积为: (单位面积)
数学八年级上册1 探索勾股定理精品ppt课件: 这是一份数学八年级上册1 探索勾股定理精品ppt课件,共36页。
初中数学北师大版八年级上册1 探索勾股定理优质课件ppt: 这是一份初中数学北师大版八年级上册1 探索勾股定理优质课件ppt,共31页。PPT课件主要包含了勾股树,导入新知,素养目标,勾股定理的探索,做一做,探究新知,数格子,单位面积,4分析填表数据,勾股定理等内容,欢迎下载使用。
数学八年级上册1 探索勾股定理课文内容ppt课件: 这是一份数学八年级上册1 探索勾股定理课文内容ppt课件,共23页。PPT课件主要包含了探索勾股定理,Contents,情境导入,巩固练习,课堂小结,新知探究,作业布置,测量法,数学小史,2符号语言等内容,欢迎下载使用。













