初中数学北师大版八年级上册1 探索勾股定理精品习题

1.1《探索勾股定理》同步练习1

一、选择题

1. 在直角三角形中，若勾为3，股为4，则弦为（　　）

A. 5 B. 6 C. 7 D. 8

2. 下列说法正确的是（    ）

A. 若a，b，c是△ABC的三边，则a2＋b2＝c2

B. 若a，b，c是Rt△ABC的三边，则a2＋b2＝c2

C. 若a，b，c是Rt△ABC的三边，∠A＝90°，则a2＋b2＝c2

D. 若a，b，c是Rt△ABC的三边，∠A＝90°，则c2＋b2＝a2

3. 如图，做一个宽80厘米，高60厘米的长方形木框，需在相对角顶点加一根加固木条，则木条长为（ ）

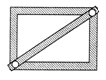
A. 90厘米 B. 100厘米 C. 105厘米 D. 110厘米

4.如图，a、b、c分别表示直角三角形的三边向外作的正方形的面积，下列关系正确的是（　　）

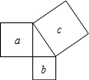
A．a+b=c B．a2+b2=c2 C ．ab=c D．a+b=c2

5．已知一个直角三角形的两条直角边长分别为6和8，则第三边长的平方是（　　　）

A．36 B．64 C．100 D．100或28

6．下列四组数：（1）0.6，0.8，1；（2）9，40，41；（3）7，24，25；（4）4，5，6．其中勾股数的组数为（　　）

A．4组 B．3组 C．2组 D．1组

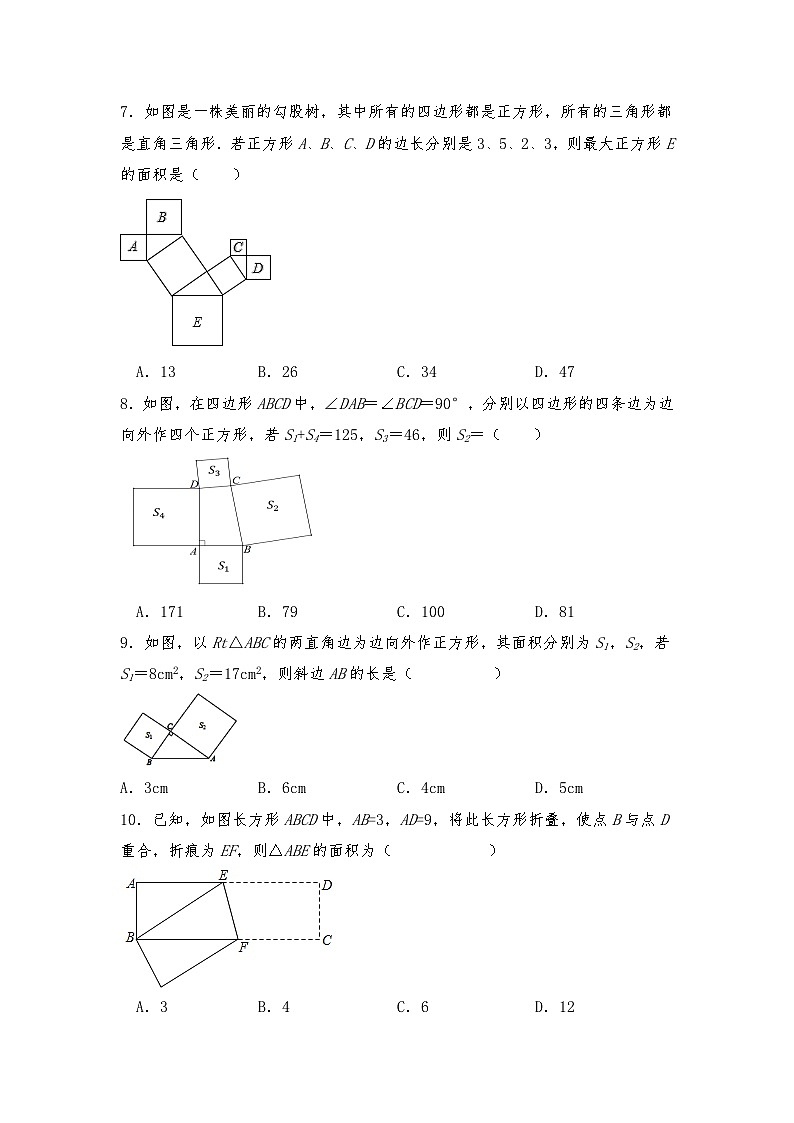
7．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（　　）

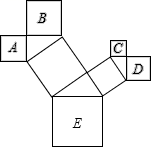
A．13 B．26 C．34 D．47

8．如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形的四条边为边向外作四个正方形，若S1+S4＝125，S3＝46，则S2＝（　　）

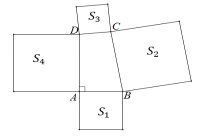
A．171 B．79 C．100 D．81

9．如图，以Rt△ABC的两直角边为边向外作正方形，其面积分别为S1，S2，若S1＝8cm2，S2＝17cm2，则斜边AB的长是（     ）

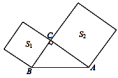
A．3cm B．6cm C．4cm D．5cm

10．已知，如图长方形ABCD中，AB=3，AD=9，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（      ）

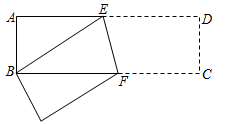
A．3 B．4 C．6 D．12

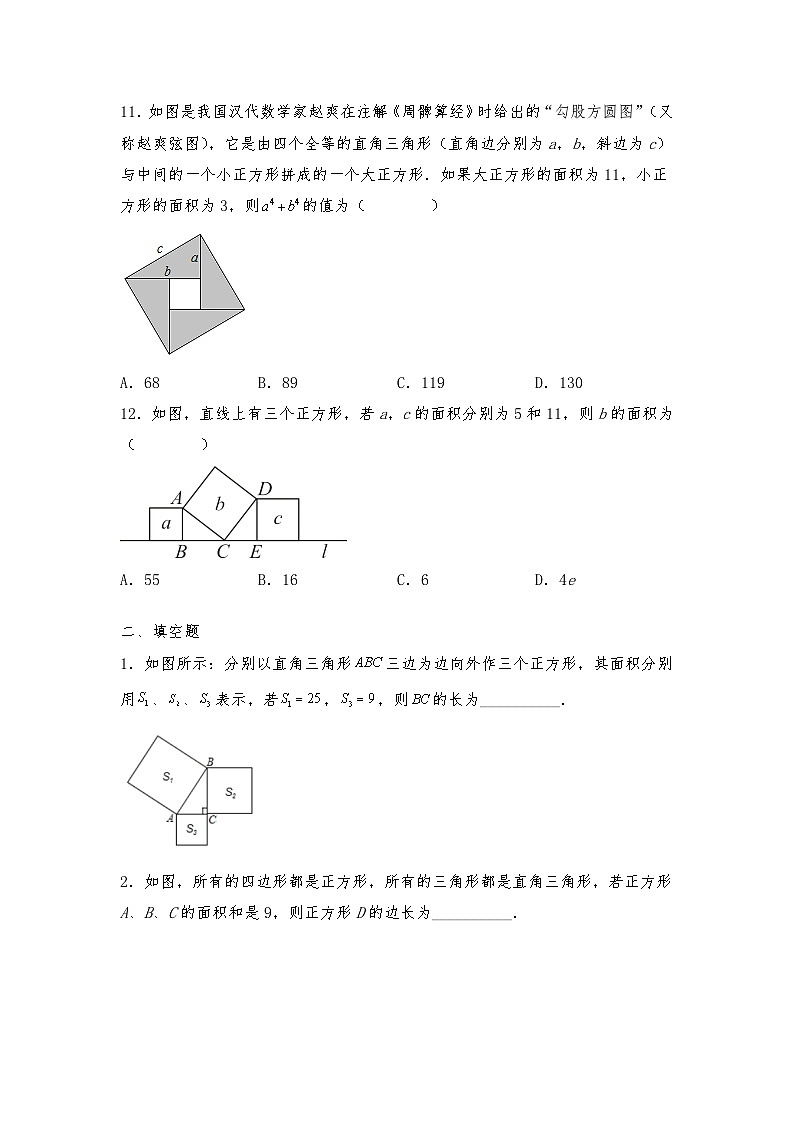
11．如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“勾股方圆图”（又称赵爽弦图），它是由四个全等的直角三角形（直角边分别为a，b，斜边为c）与中间的一个小正方形拼成的一个大正方形．如果大正方形的面积为11，小正方形的面积为3，则的值为（    ）

A．68 B．89 C．119 D．130

12．如图，直线上有三个正方形，若a，c的面积分别为5和11，则b的面积为（    ）

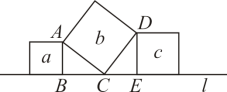
A．55 B．16 C．6 D．4e

二、填空题

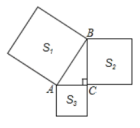
1．如图所示：分别以直角三角形三边为边向外作三个正方形，其面积分别用、、表示，若，，则的长为__________．

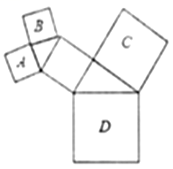
2．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C的面积和是9，则正方形D的边长为__________．

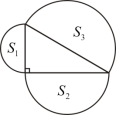
3．如图，直角三角形三边上的半圆面积之间的关系是________．

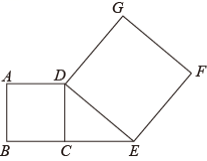
4．如图，线段CE的长为3cm，延长EC到B，以CB为一边作正方形ABCD，连接DE，以DE为一边作正方形DEFG，设正方形ABCD的面积为，正方形DEFG的面积为，则的值为______．

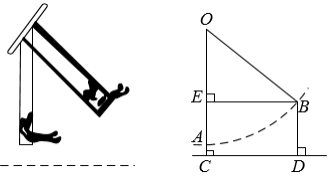
5．学习完《勾股定理》后，尹老师要求数学兴趣小组的同学测量学校旗杆的高度．同学们发现系在旗杆顶端的绳子垂到了地面并多出了一段，但这条绳子的长度未知．如图，经测量，绳子多出的部分长度为1米，将绳子沿地面拉直，绳子底端距离旗杆底端4米，则旗杆的高度为______米．

6．如图，在Rt△ABC中，∠C=90°，若AB=7，则正方形ADEC和正方形BCFG的面积和是______．

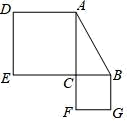
7．明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地……”翻译成现代文为：如图，秋千绳索OA悬挂于O点，静止时竖直下垂，A点为踏板位置，踏板离地高度为一尺（AC＝1尺）．将它往前推进两步（EB⊥OC于点E，且EB＝10尺），踏板升高到点B位置，此时踏板离地五尺（BD＝CE＝5尺），则秋千绳索（OA或OB）长______尺．

三、解答题

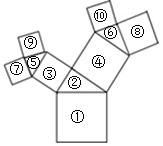
1．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，请在图中找出若干个图形，使得它们的面积之和恰好等于最大正方形①的面积，尝试给出两种以上的方案．

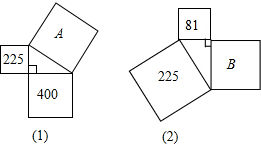
2．求图中字母所代表的正方形的面积．

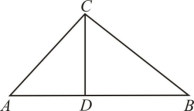
3．如图，在ABC中，∠ACB＝90°，CD⊥AB于点D，AC＝12cm，BC＝16cm，求CD的长．

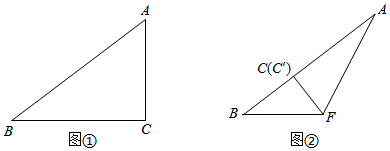
4．如图①，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，将此图形折叠得图②，折痕为AF，且点C恰好落在边AB上点C′处，求C′F的长．

5．如图，，，，．

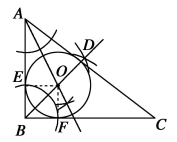
（1）请你用无刻度的直尺和圆规，作出的内切圆（保留作图痕迹，不要求写作法）；

（2）求的半径长．

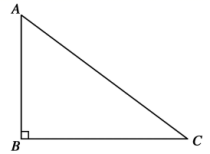
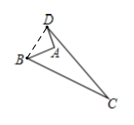
6．如图，四边形ABCD中，AB⊥AD，已知AD＝3cm，AB＝4cm，CD＝13cm，BC＝12cm，求四边形ABCD的面积．

答案

一、选择题

A．D. B．A．C．C．D．B．D．C.B．B．

二、填空题

1.  4．    2.3     3.．   4．﹣9cm2．

5．7.5．   6．49．  7．．

三、解答题

1.解：设正方形①、③、④的边长分别是a、b、c，

则正方形①的面积＝a2，正方形③的面积＝b2，正方形④的面积＝c2，

又∵c2+b2＝a2，

∴③和④的面积之和恰好等于最大正方形①的面积．

同理，④⑨⑦的面积恰好等于最大正方形①的面积．

类似的还有：⑧⑩⑨⑦或⑧⑩③．

2.解：A的边长为直角三角形的斜边，则A的边长的平方等于两直角边边长的平方和，两条直角边的平方分别为：225和400，

A的面积＝225+400＝625，

同理B的边长为直角三角形的直角边，则存在B的边长的平方等于斜边的平方减去另一直角边的平方，斜边的平方为225，直角边的平方为81

B的面积为225﹣81＝144．

3.∵∠ACB=90°，AC=12cm，BC=16cm，

∴AB=20cm，

根据直角三角形的面积公式，得：

，

∴．

4.解：由折叠得：AC'=AC=6，C'F⊥AB，CF=C'F，

在Rt△ABC中，∠C=90°，BC=8，AC=6，

∴AB=10，

∴BC'=10﹣6=4，

在Rt△BC'F中，设C'F=x，则BF=8﹣x，

∴x2+42=(8﹣x)2，

解方程得：x=3．

即C'F=3．

5.解：（1）如图所示，

（2）过作于点，于点，

∴，，

又∵，

∴四边形是矩形（有三个角是直角的四边形是矩形）

∵，

∴矩形是正方形，

∴，

设的半径为，则，

∵是的内切圆，

∴，（从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角）

∵中，，，，

∴，

∴，

∴．

答：圆的半径长为2.

6.解：连接BD，

AB⊥AD，

，

在中，

在中，，

是直角三角形，