初中数学人教版八年级上册15.3 分式方程公开课第一课时教学设计及反思

15.3分式方程（1）教学设计

一、教学目标：

 1．了解分式方程的概念, 和产生增根的原因.

2．掌握分式方程的解法，会解可化为一元一次方程的分式方程，会检

验一个数是不是原分式方程的解.

二、重点难点：

 1．重点：会解可化为整式方程的分式方程，会检验一个数是不是

原方程的增根.

 2．难点：会解可化为整式方程的分式方程，会检验一个数是不是

原方程的增根.并理解产生增根的原因

三、教学过程：

复习巩固

问题：1.我们已经学习了哪些的方程？

师生活动：教师提问，学生回答，教师适当补充。

一元一次方程  二元一次方程（组）

问题：下列哪些是一元一次方程,哪些是二元一次方程?两类方程有什么共同的特点?

①3x-2=5,  ②x+y=4,

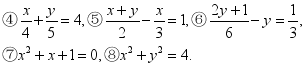
师生活动：教师提问，学生回答，教师适当补充。

一元一次方程有:①③⑥

二元一次方程有:②④⑤

共同特点:方程左右两边都是整式.

问题：2.解方程的基本思想是什么？

一元一次方程转化x=a

二元一次方程（组）转化一元一次方程转化x=a

设计意图：从旧知识入手，一个可以把我方程的特征，另外可以启发学生去找到新旧知识的联系，从而更好的学习新知识。

3.实际问题引入新课  

一艘轮船在静水中的最大航速为30km/h,它沿江以最大航速顺流航行90km所用时间,与以最大航速逆流航行60km所用时间相等,江水的流速为多少?

解:设江水的流速为 v 千米/时，

根据题意，得

归纳定义：

像这样，分母中含有未知数的方程叫做分式方程.

以前学过的分母里不含有未知数的方程叫做整式方程.

设计意图：从实际问题入手，强调数学知识与生活的密切联系，也为后面的用方程解决实际问题埋下伏笔。

练习1：下列方程中，哪些是分式方程？哪些整式方程？

师生活动：教师提问，学生回答，教师适当补充。

设计意图：通过辨析题目，加强对新知识的概念的及时理解，也便于找到新旧知识之间的联系和区别。

探究一：如何解分式方程？

师生活动：学生自主探究，老师相应指导。

试着解一下这个分式方程，如果没成功，说说你遇到的困难;如果成功，介绍一下你的作法.

思考：（1）如何把分式方程转化为整式方程呢？

（2）在方程两边乘以什么样的式子才能把每一个分母都约去呢？

（3）这样做的依据是什么？

解：方程两边乘(30+v)(30-v) ，

得：

检验: 将v=6代入分式方程,

左边=2.5=右边，

所以v=6是原分式方程的解

解分式方程思想方法：化归思想

分式方程

转  ↓

  去分母

化  ↓

整式方程

转  ↓ 解方程

化  X=a

↓

检  验

设计意图：通过自主探究培，养学生分析问题，解决问题的能力。通过适当的问题设计让不同等级的学生都能参与进来。明确解方程的中使用的化归思想。

练习2解分式方程：

解：两边同乘以最简公分母(x-5)(x+5)，

得：x+5=10

x=5

检验：

将x=5代入x-5,x2-25的值都为0，

相应分式无意义.所以x=5不是原分式方程的解.

去分母变形是否引起分式方程解的变化，主要取决于所乘的最简公分母是否为0

练习2解分式方程：

解：两边同乘以最简公分母(x-5)(x+5)，

得：x+5=10

     x=5

检验：

当x=5时， (x-5)(x+5) =0，

因此x=5不是原分式方程的解.

所以，原分式方程的无解.

对比归纳：检验的方法主要有两种

（1）将整式方程的解代入原分式方程，看左右两边是否相等；

（2）将整式方程的解代入最简公分母，看是否为0．

显然，第2种方法比较简便！

归纳总结：解分式方程的一般步骤：

（1）去分母；（2）解整式方程；（3）检验．

注意：由于去分母后解得的整式方程的解不一定是原分式方程的解，所以必须检验．

设计意图：通过两种检验方法的对比，明确了检验在解分式方程中的必要，强调解分式方程的基本步骤，并了解到解分式中产生增根的原因。

例1:解方程

解:方程两边乘 x(x-3),  得 

          2x = 3(x-3)

解得    x = 9,  

检验:当x=9时, x(x-3)≠0.

∴原分式方程的解为 x=9.

练习3　解下列方程：

解分式方程容易出现的错误有：

(1)去分母时，原方程的整式部分漏乘

(2)约去分母后，分子是多项式时，没有注意添括号(因分数线有括号的作用）  

(3)漏检验

设计意图：通过学生的做题体验，归纳出易错点，培养学生的数学语言表达能力。也突破本节课的易错点。

课堂小结

1. 解分式方程的思路是

          转化

分式方程   →  整式方程

2. 解分式方程的一般步骤：

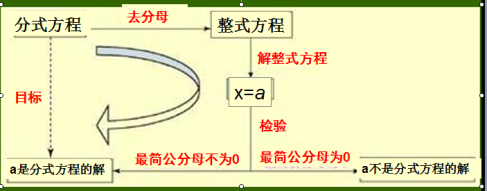
设计意图：通过图表的形式展示分式方程的解题步骤，并提炼出解题思路。培养学生化归的数学思想

课后作业

课本相应内容